一,题目描述
将编号为 1~10 的 10 本书排放在书架上,要求编号相邻的书不能放在相邻的位置。请计算一共有多少种不同的排列方案。
二,答案提交
注意,需要提交的是一个整数,不要填写任何多余的内容。
三,答案代码
提供了两种方法,一种是暴力求解,一种是check()方法
#作业四 图书管理
方法一 暴力求解
import itertools
book = [1,2,3,4,5,6,7,8,9,10]
sum = 0
for i in itertools.permutations(book,10):
if abs(i[0]-i[1])!=1 and abs(i[1]-i[2])!=1 and abs(i[2]-i[3])!=1 and abs(i[3]-i[4])!=1 and abs(i[4]-i[5])!=1 and abs(i[5]-i[6])!=1 and abs(i[6]-i[7])!=1 and abs(i[7]-i[8])!=1 and abs(i[8]-i[9])!=1:
sum += 1
print(sum)方法二 check法
import itertools
res = 0
x = [i for i in range(10)]
def check(a):
for i in range(9):
if abs(a[i]-a[i+1]) == 1:
return False
return True
for i in itertools.permutations(x, 10):
if check(i):
res += 1
print(res)
四,题目解读??
题目很好理解,10本书编号1~10,相邻号码图书不相邻,问图书排列序列的可能性。
五,代码解读
itertools库的用法讲解在第六部分
import itertools #引入itertools库里的permutations函数列出可能序列
book = [1,2,3,4,5,6,7,8,9,10] #给图书编号
sum = 0 #计数,for循环每循环一次,就是一种可能序列,用于累积计数
for i in itertools.permutations(book,10):
if abs(i[0]-i[1])!=1 and abs(i[1]-i[2])!=1 and abs(i[2]-i[3])!=1 and abs(i[3]-i[4])!=1 and abs(i[4]-i[5])!=1 and abs(i[5]-i[6])!=1 and abs(i[6]-i[7])!=1 and abs(i[7]-i[8])!=1 and abs(i[8]-i[9])!=1:
#暴力求解,列举出所有不成立序列,图书序号差如果为1就证明相邻
sum += 1
print(sum)import itertools
sum = 0
x = [i for i in range(10)] #x是1到10的一个列表
def check(x):
for i in range(9):
if abs(x[i]-x[i+1]) == 1: #判断是否相邻,abs()是求绝对值,x[i]是第i项
return False
return True
for j in itertools.permutations(x, 10):#列举出所有序列,并用check()函数判断是否符合条件
if check(j):
sum += 1 #每循环一次加1
print(sum)?六,itertools
在python中,itertools库的permutations(组合)方法用于列举排列组合里的所有可能
标准语法itertools.permutations(iterable[, r])
括号里左边是需要排列组合的对象(图书),是一个字符串或列表,右边的是每次去多少个元素排列组合,题目就是去了10个。
如itertools.permutations('ABC',2)就是将ABC每次取两个来排列,如下:
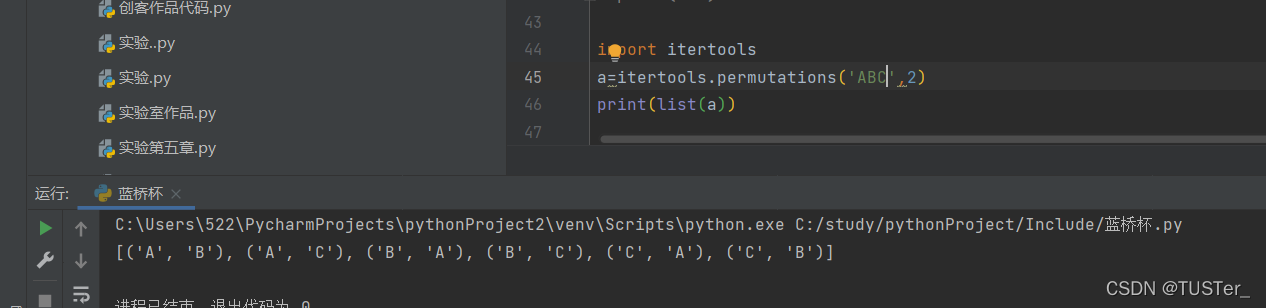
?结语:额,今天别想白嫖,对于有些题目,能暴力求解就去暴力求解,这样更加节省时间,记得一键三连!!!
今日一笑:《逗的他(她)们满脸黑线头》
说有那么几个人在踢足球,分红蓝两方,红队守门员说:“我是铁门,你们球进不来1这时,蓝队守门员冷笑一声,“我是钢门1。。。