[数据结构与算法]Leetcode 专题训练 递归和分治（三）

深度理解递归-练习题

912. 排序数组

归并排序

尝试的复习了昨天的归并排序，重新理解了为什么要用while i <= mid 或者while j <= right对剩下的数组进行合并。而不能直接拼接，那样会有问题。另外也理解了为什么不是nums=temp，而是nums[left:right+1]=temp。因为在归并的时候，left和right都是原数组的一部分。我们只能修改一部分的数组序列。

def sortArray(self, nums: List[int]) -> List[int]:
        def merge(left, mid, right, nums):
            i, j = left, mid + 1
            temp = []
            while i <= mid and j <= right:
                if nums[i] < nums[j]:
                    temp.append(nums[i])
                    i += 1
                else:
                    temp.append(nums[j])
                    j += 1
            while i <= mid:
                temp.append(nums[i])
                i += 1
            while j <= right:
                temp.append(nums[j])
                j += 1
            nums[left:right+1] = temp

        def recur(left, right, nums):
            if left >= right: return
            mid = (left + right) // 2
            recur(left, mid, nums)
            recur(mid+1, right, nums)
            merge(left, mid, right, nums)
        
        recur(0, len(nums)-1, nums)
        return nums

下面是K神的归并排序，思路和代码：








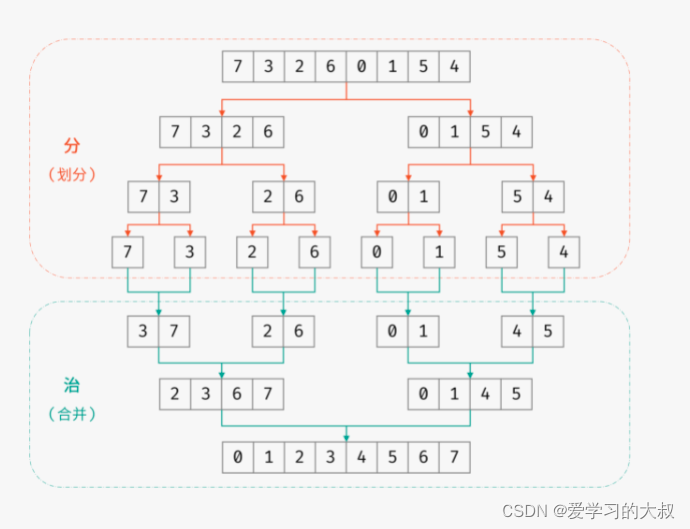
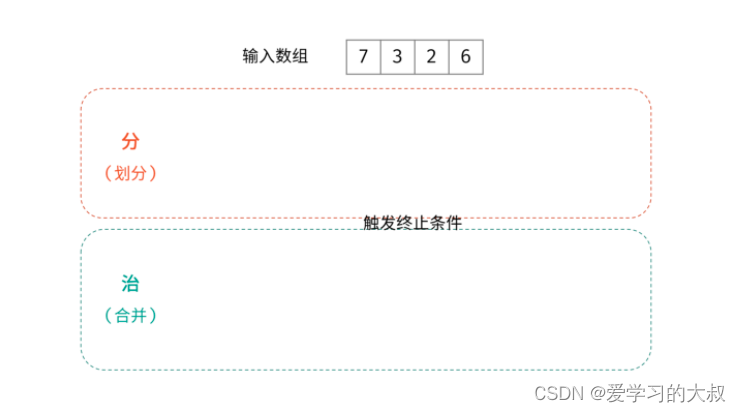
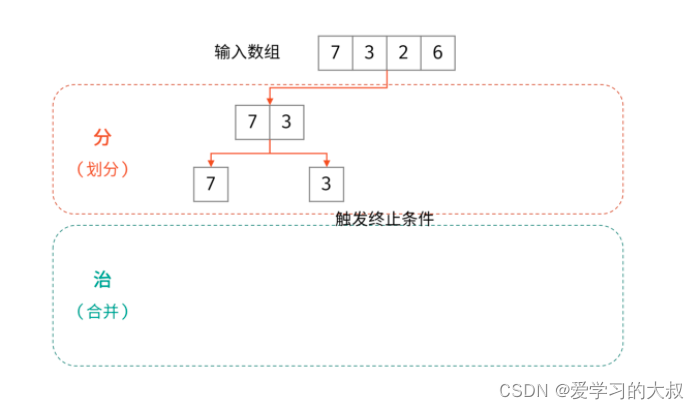
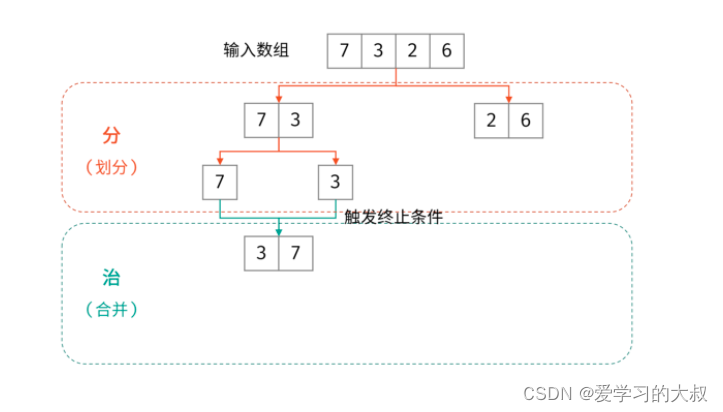
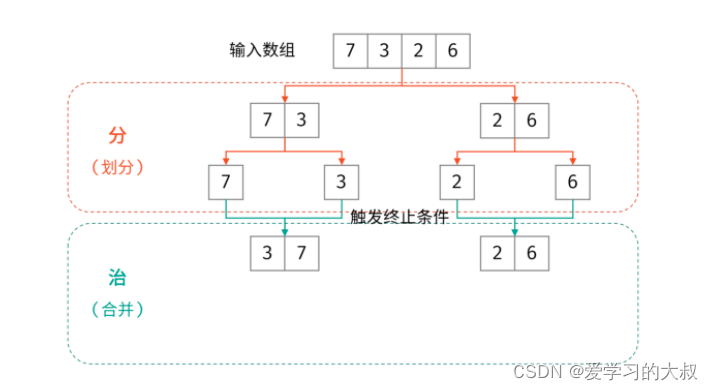
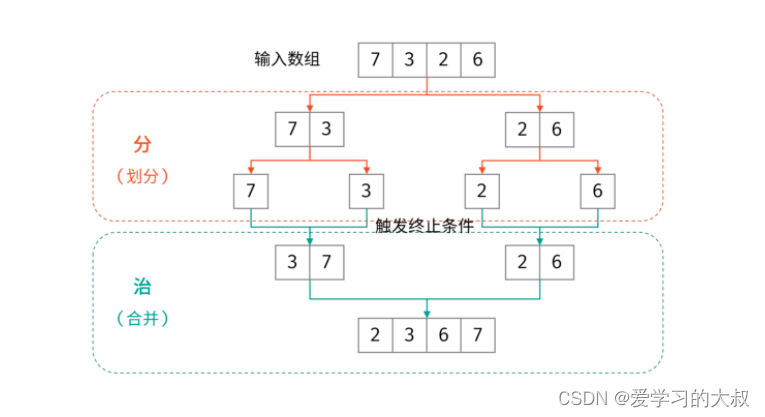
大佬代码：

def sortArray(self, nums: List[int]) -> List[int]:
        def merge_sort(nums, l, r):
            # 终止条件
            if l >= r: return
            # 递归划分数组
            m = (l + r) // 2
            merge_sort(nums, l, m)
            merge_sort(nums, m + 1, r)
            # 合并子数组
            tmp = nums[l:r + 1]       # 暂存需合并区间元素
            i, j = 0, m - l + 1       # 两指针分别指向左/右子数组的首个元素
            for k in range(l, r + 1): # 遍历合并左/右子数组
                if i == m - l + 1:
                    nums[k] = tmp[j]
                    j += 1
                elif j == r - l + 1 or tmp[i] <= tmp[j]:
                    nums[k] = tmp[i]
                    i += 1
                else:
                    nums[k] = tmp[j]
                    j += 1
        merge_sort(nums, 0, len(nums)-1)
        return nums

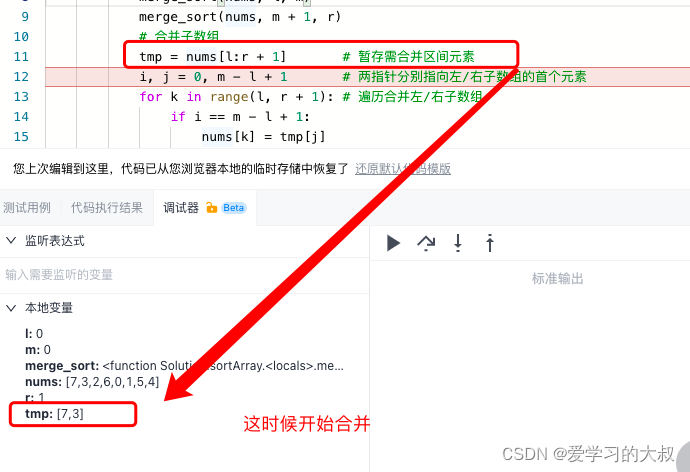
K神的代码，走debug勉强可以看懂，但是还没自己手写过。

快速排序

我写的，就是实践总是超时。

def sortArray(self, nums: List[int]) -> List[int]:
        def quicksort(left, right, nums):
            if left >= right: return
            pivot = nums[left]
            start, end = left, right

            while left < right:
                while left < right and nums[right] >= pivot:
                    right -= 1
                nums[right], nums[left] = nums[left], nums[right]
                while left < right and nums[left] <= pivot:
                    left += 1
                nums[left], nums[right] = nums[right], nums[left]

            quicksort(start, right-1, nums)
            quicksort(left+1, end, nums)

        quicksort(0, len(nums)-1, nums)
        return nums

K神的方法也通不过，也是超时。

def sortArray(self, nums: List[int]) -> List[int]:
        def quick_sort(nums, l, r):
            # 子数组长度为 1 时终止递归
            if l >= r: return
            # 哨兵划分操作
            i = partition(nums, l, r)
            # 递归左（右）子数组执行哨兵划分
            quick_sort(nums, l, i - 1)
            quick_sort(nums, i + 1, r)
            
        def partition(nums, l, r):
            # 以 nums[l] 作为基准数
            i, j = l, r
            while i < j:
                while i < j and nums[j] >= nums[l]: j -= 1
                while i < j and nums[i] <= nums[l]: i += 1
                nums[i], nums[j] = nums[j], nums[i]
            nums[l], nums[i] = nums[i], nums[l]
            return i
        
        quick_sort(nums, 0, len(nums) - 1)
        return nums