[数据结构与算法]回溯——子集问题

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

解题思路：回溯

与组合问题相比，组合问题收集的是抽象树结构的叶子节点，而自己问题则是需要收集所有节点。

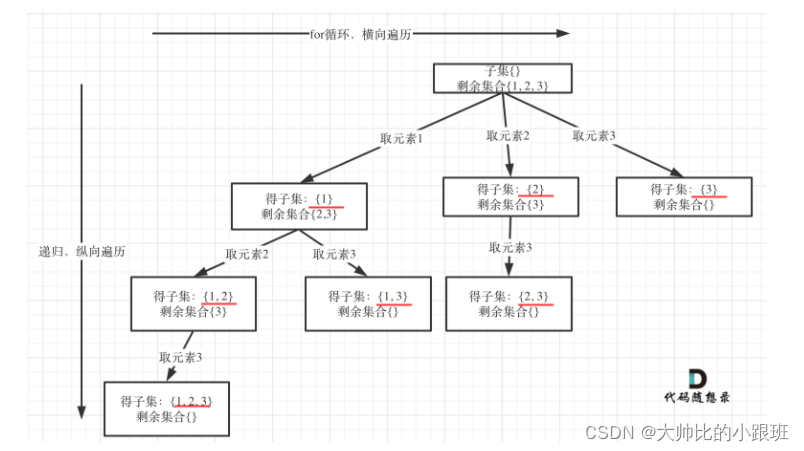
代码和提交结果如下：

?

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        //回溯法
        List<List<Integer>> res = new ArrayList();
        Stack<Integer> paths = new Stack();
        backTracking(res,paths,0,nums);
        return res;
    }
    private void backTracking(List<List<Integer>> res , Stack<Integer> paths ,int startIndex , int[] nums ){
        res.add(new ArrayList(paths));            
            for(int i = startIndex ; i < nums.length ; i++){
                paths.push(nums[i]);
                backTracking(res,paths,i+1,nums);
                paths.pop();
            }
        }
}

其实可以有递归的判出条件是，startIndex >= nums.lengths，但是因为需要收集所有节点，和for循环结束后完成递归是一个效果，所以没有加。?

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

解题思路：这道题目和78.子集?(opens new window)区别就是集合里有重复元素了，而且求取的子集要去重。属于“树层去重”，在传入数组之前需要对数组进行sort，然后使用used数组进行去重，如果 i > startIndex && nums[i-1] == nums[i] && used[i-1] == false，则说明nums[i]同层已经使用过了，需要continue跳过。

代码和实现结果如下：

class Solution {
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        if(nums.length == 0){
            return new ArrayList();
        }
        List<List<Integer>> res = new ArrayList();
        Stack<Integer> paths = new Stack();
        boolean used[] = new boolean[nums.length];
        Arrays.sort(nums);
        backTracking(res,paths,0,nums,used);
        return res;
    }
    private void backTracking(List<List<Integer>> res , Stack<Integer> paths ,int startIndex , int[] nums ,boolean[] used){
        res.add(new ArrayList(paths));   
        for(int i = startIndex ; i < nums.length ; i++){
            if(i > startIndex && nums[i-1] == nums[i] && used[i-1] == false){
                continue;   
            }
            paths.push(nums[i]);
            used[i] = true;
            backTracking(res,paths,i+1,nums,used);
            used[i] = false;
            paths.pop();
        }
    }
}

?

总结： 回溯部分分为? 组合、子集、排列、分割字符串、棋盘问题、递增子序列几个部分，重点在于理解回溯的模板，以及各种去重、剪枝操作。如果可以排序，树层去重可以用used[ ]。