目录
?一、前言
①什么是二分查找?
????????二分查找是在有序表中查找目标元素的算法,其基本思想其实就是“猜数字游戏”——已知某个数k在0~1000之内,如何猜出这个数具体是多大呢?二分查找是这样处理的:
- k大于500吗?不大于。所以我们将数据范围压缩到0~500之间
- k大于250吗?大于。所以我们将数据范围压缩到250~500之间
- k大于375吗?大于。所以我们将数据范围压缩到375~500之间
- ……
????????如此不断的压缩范围数据的范围,最后当只剩下1个数据时答案已经被锁定了(当然如果运气好,那我们选定的“折半值”可能就是k了),可以看到二分查找不断折半缩小待查找的数据范围因此二分查找也被翻译成“折半查找”。
②二分查找有多优秀?
????????试想如果我们从0~1000一一枚举,那我们最倒霉需要猜1000次,而使用二分的思路最坏也只?要需要10次(怎么算出来的呢?![]() ,而
,而![]() ,所以10次就可以包含完0~1000的所有情况)。如果数据范围更大些,那效率的差距将会更加的突出。
,所以10次就可以包含完0~1000的所有情况)。如果数据范围更大些,那效率的差距将会更加的突出。
假设检查一个元素需要1ms,那我们可以得到以下的表格:
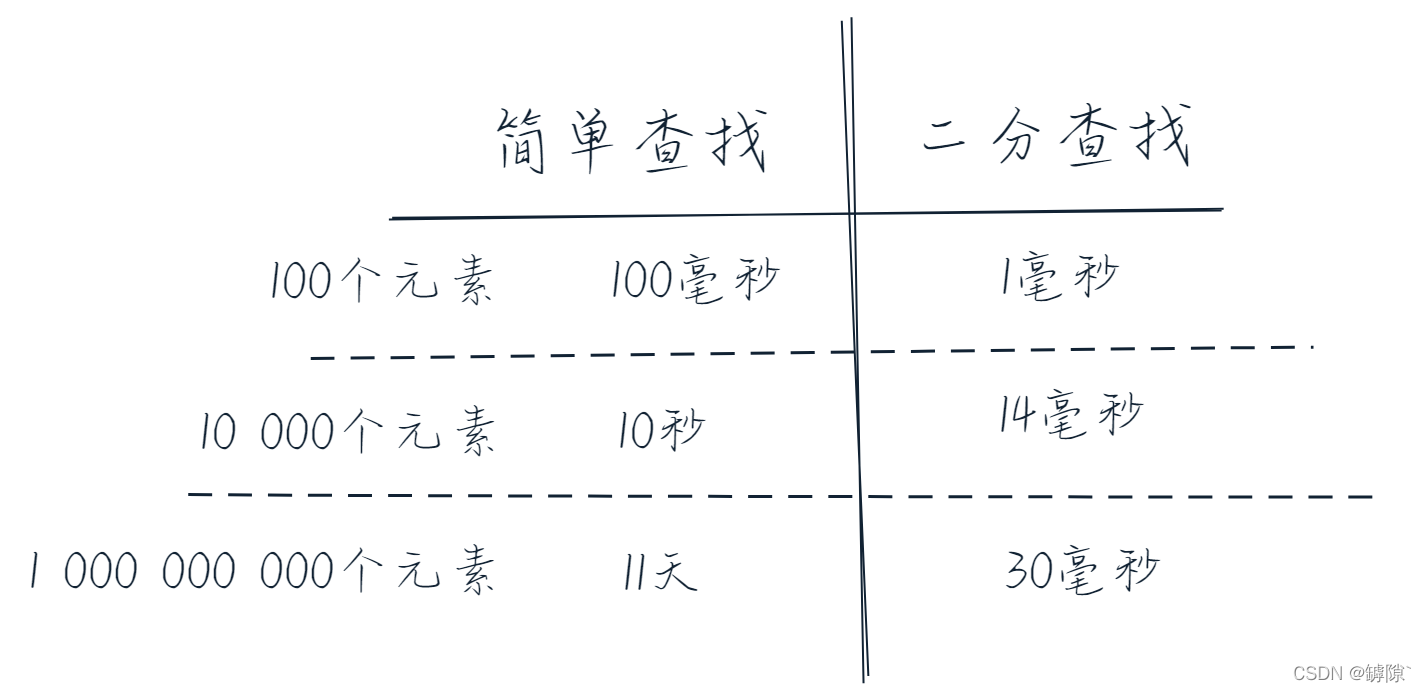
? ? ? ? ?从这个实际问题中抽象出我们的算法,一一猜数对应着暴力枚举法,它的时间复杂度为![]() ,相比之下,?二分查找的时间复杂度为
,相比之下,?二分查找的时间复杂度为![]() ,所以是相当优秀漂亮的算法。
,所以是相当优秀漂亮的算法。
③使用前提
? ? ? ? 使用二分查找的前提是原数据是一个有序表,即具有单调性。所以说检索也是排序最重要的应用之一。
④二分查找难吗?
二分查找真的很简单吗?其实也并不简单。看看 Knuth 大佬(发明 KMP 算法的那位)怎么说的:
Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky...
这句话可以这样理解:思路很简单,细节是魔鬼。
所以在这篇文章中向大家介绍二分查找的三种形式,虽然整体形式是极其相似的,但是略微的差别却带来了极大的不同。也相信学习完这篇博客大家可以熟练运用这三种形式的二分查找。
二、左闭右闭型
①代码模板
左闭右闭型是最典型的模板,也是我们学习的基础,我们依然从猜数字的角度来理解:
int Binary_search(int*arr, int target, int numsSize)// (1)
{
int left = 0; //(2)
int right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) >> 1; //(3)
if (arr[mid] < target)
left = mid + 1; //(4)
else if (arr[mid] > target)
right = mid - 1;
else
return mid;
}
return -1; //(5)
}分析:
- (1)功能:查找有序列表中target是否存在。存在则返回其下标,不存在则返回-1
- (2)left表示数组下标范围的下界,right表示数组下标范围的上界
- (3)求出中间值,也就是上面猜数字不断的“折半”值,用它来界定我们的猜测小了还是大了
- (4)如果arr[mid] < target说明猜小了,所以将下界调整到mid+1
- (5)循环结束时left > right,说明遍历了整个区间也找不到target,所以返回-1
看不懂?没关系,用下面的四张动图来帮你理解。
②动图演示
(1)检索 target = 29 是否存在
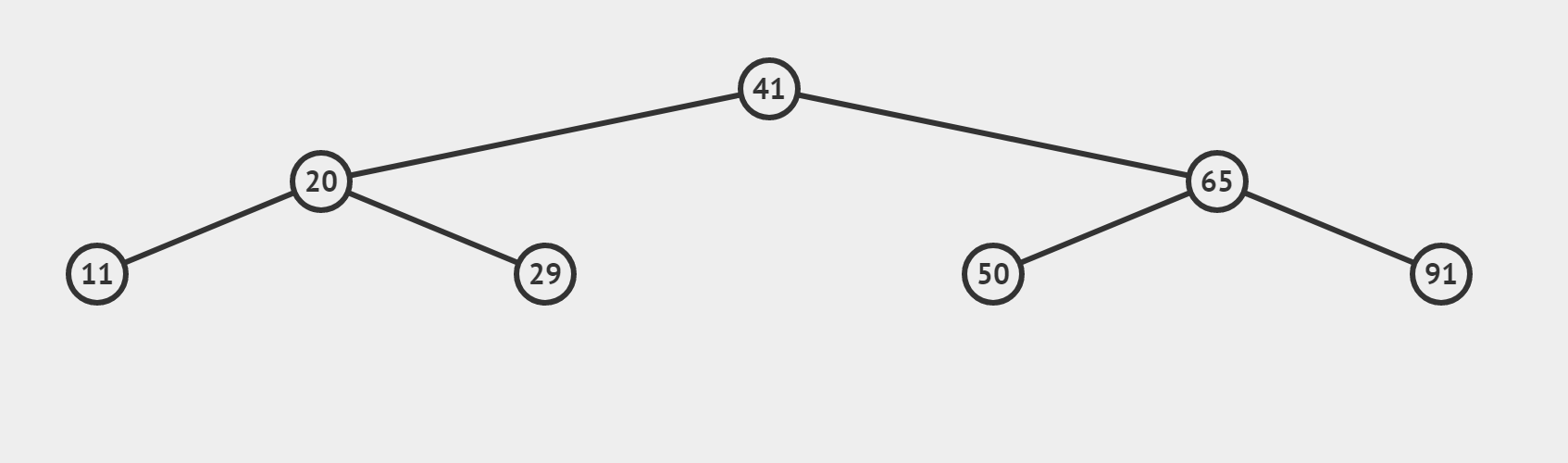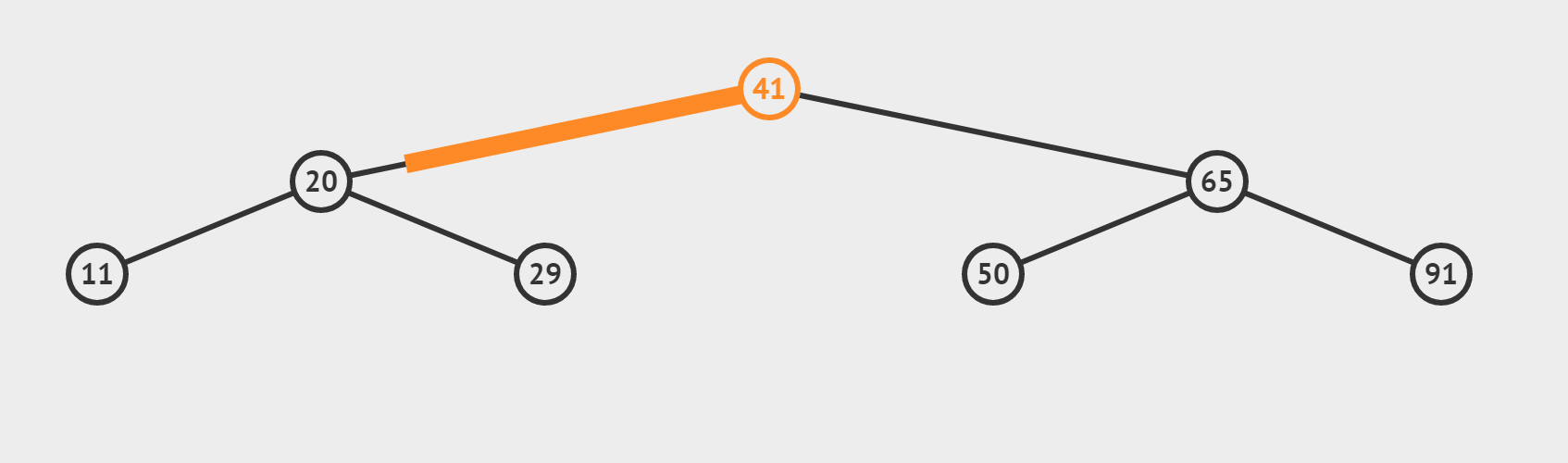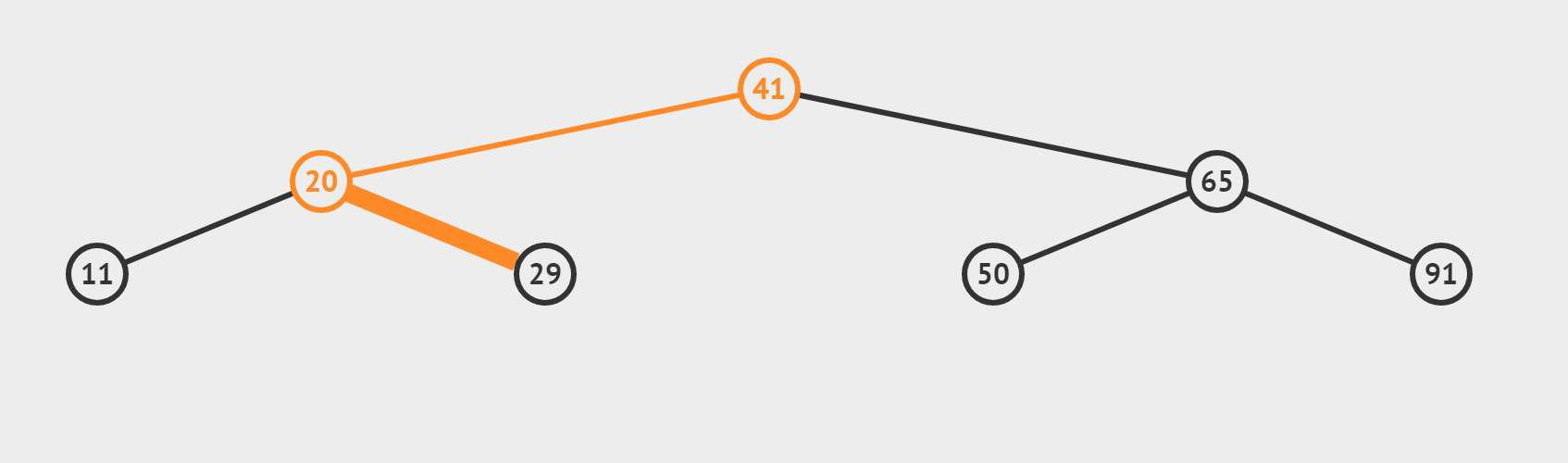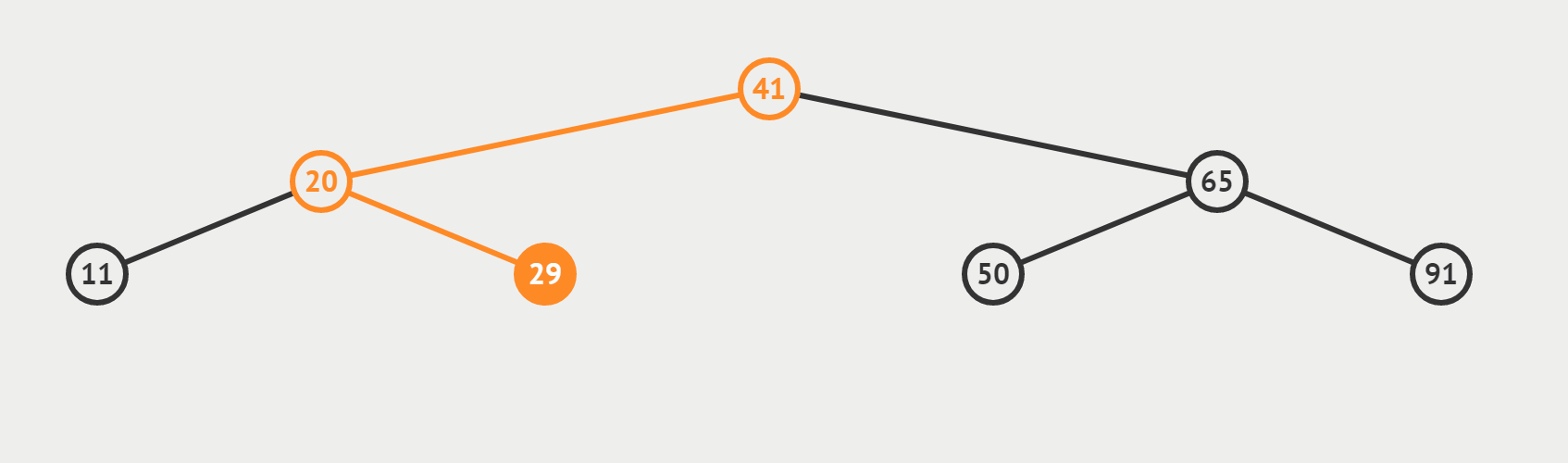
更加直观的,我们将数据数据对应到二叉树中

【如何构建的呢】
?其实就是我们对猜数字游戏的模拟,举个🌰:
- 开始 left = 0, right = 6, mid? = (left + right) / 2 = 3。由此我们创建出第一个结点41
- 如果target偏小,则 right = mid - 1 ,mid = (left?+ right) / 2 = 1.由此我们得到41的左子结点20
- 如果target偏大,则 left = mid + 1, mid = (left + right)? / 2 = 5.由此我们得到41的右子结点65
- 同样的道理我们对每个结点都分别求出其左右子结点(如果存在的话),就构造出二叉树了
【特性】
- 我们可以发现二叉树中元素自左向右依次递增,即没有改变原来的单调性
- 不难发现,遍历到二叉树的最后一层时一定有 left = right = mid (三数合一)
- 若mid的计算发生改成 (left + right + 1) /??2,构造出的二叉树的偏向会不同,读者可自行尝试?
(2)检索 target = 29 是否存在
?(3)target 找不到的情况(搜索 target = 35)
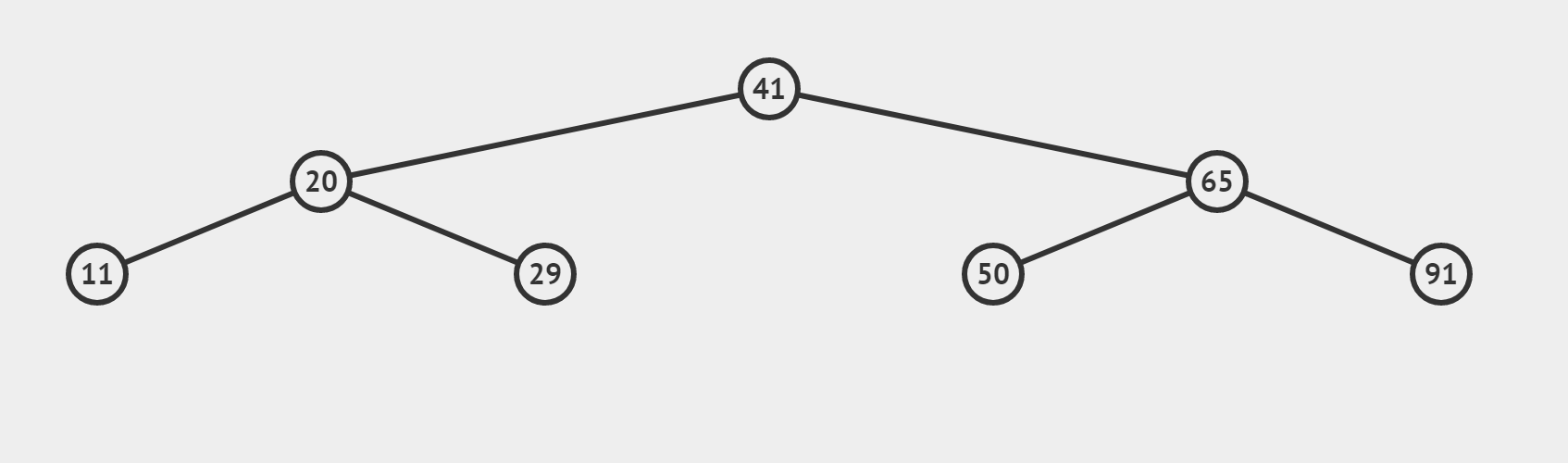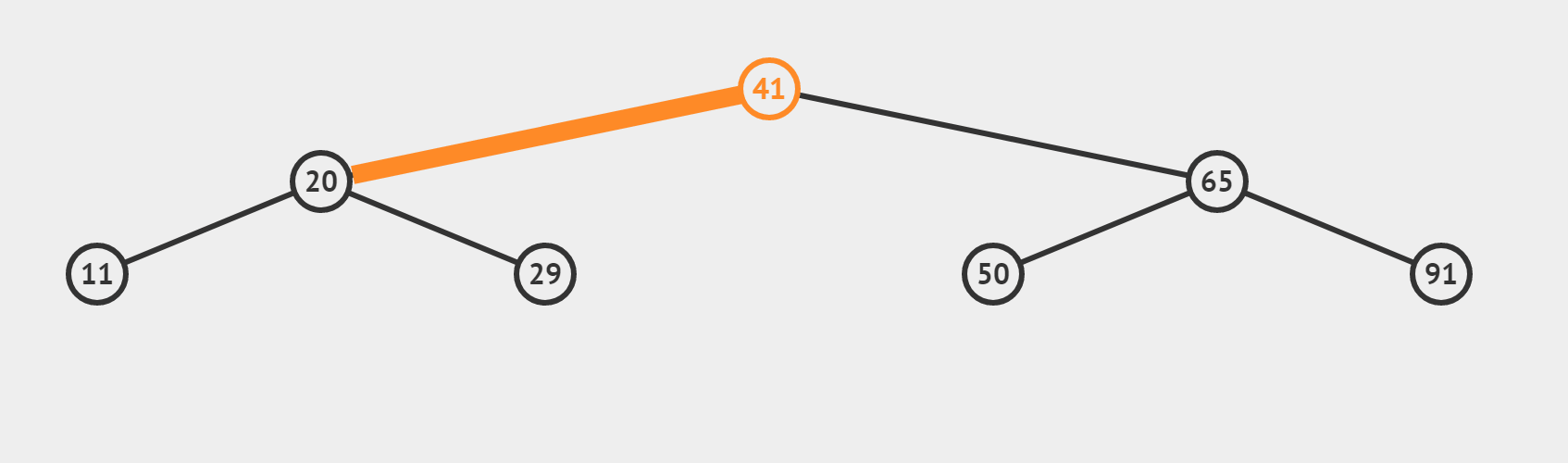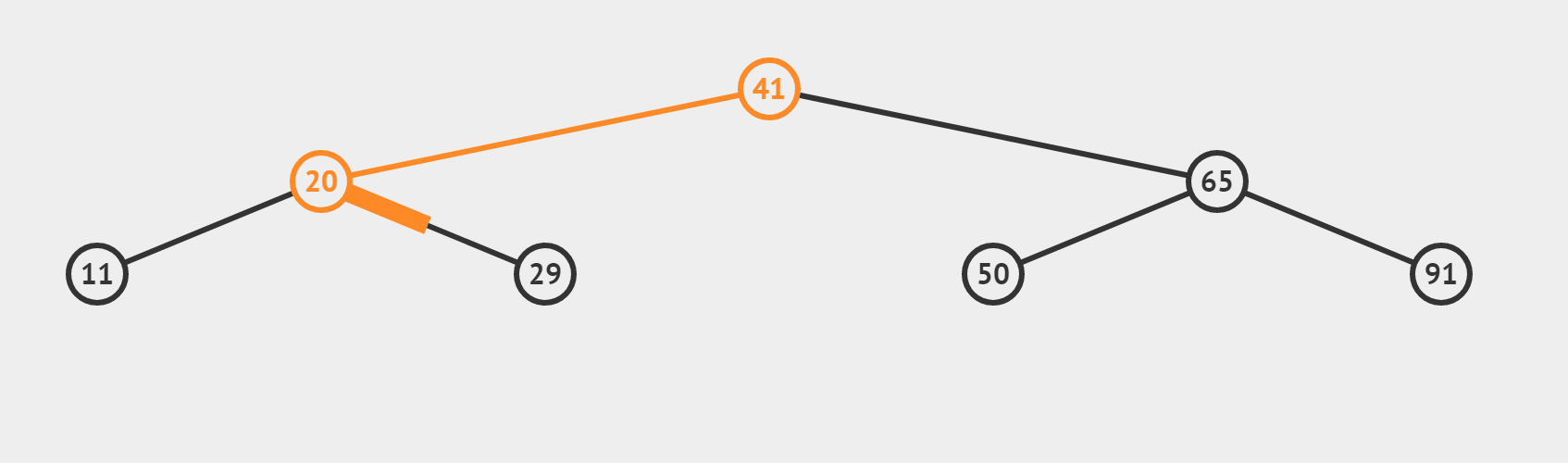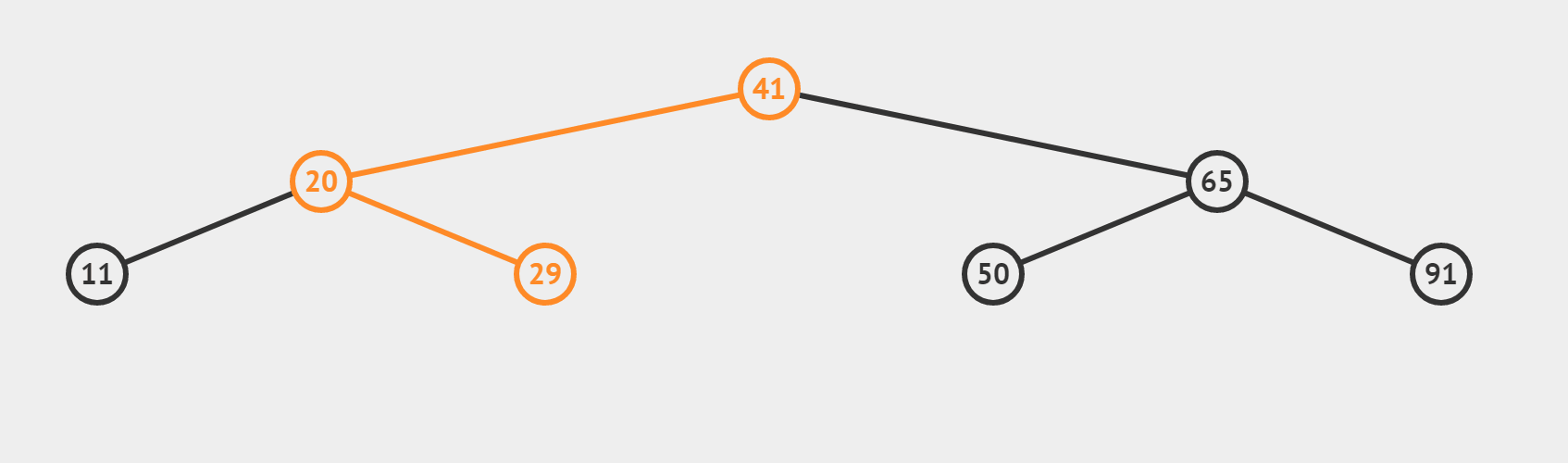
??【和情况(2)有什么区别呢】
- 若这个数是target,我们将直接返回它的下标,也即情况 (2)
- 若这个数不是我们的target,利用三数合一的结论,根据target偏大还是偏小,决定 left = mid + 1或者 right = mid-1 最终使得left > right,循环终止。所以相当于从最后一层向左或向右,“虚伸”出一条不存在的“小腿”。
(4)更复杂点的情况(采用mid = ( left + right + 1) / 2)
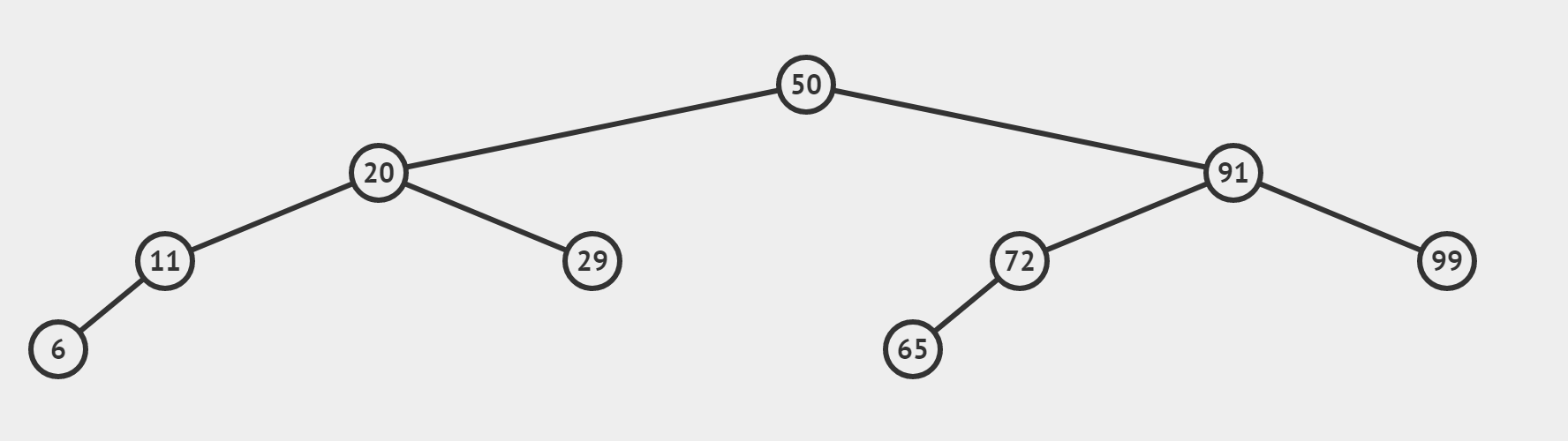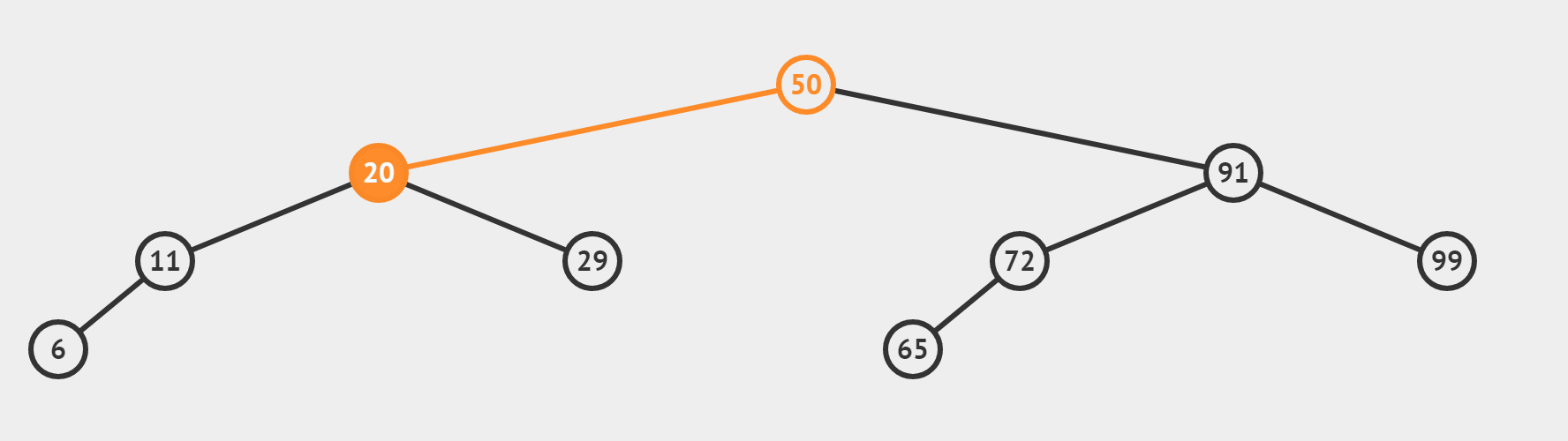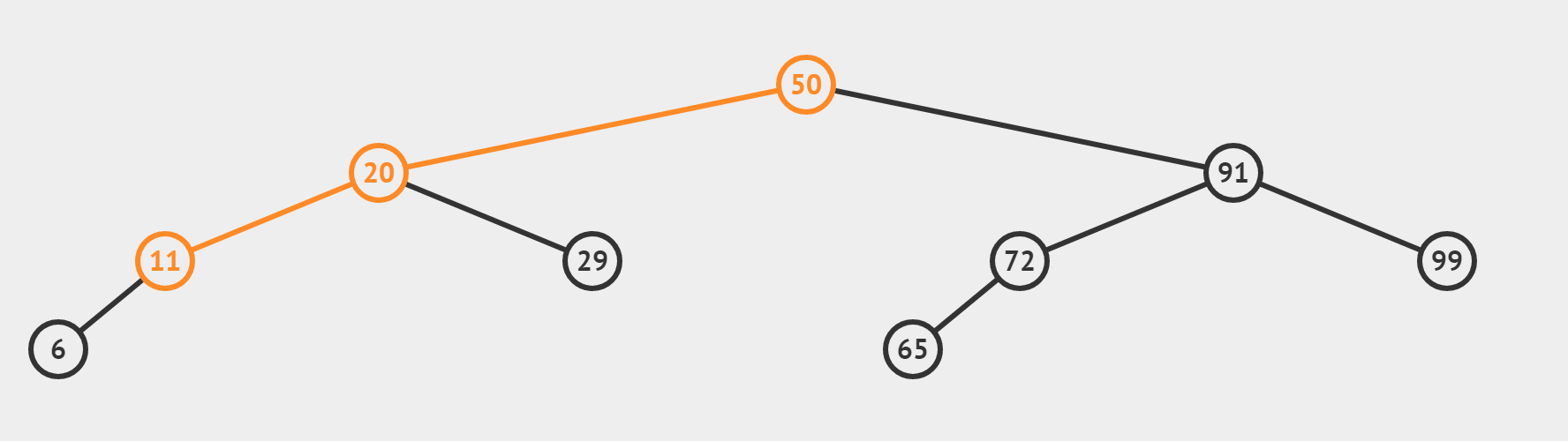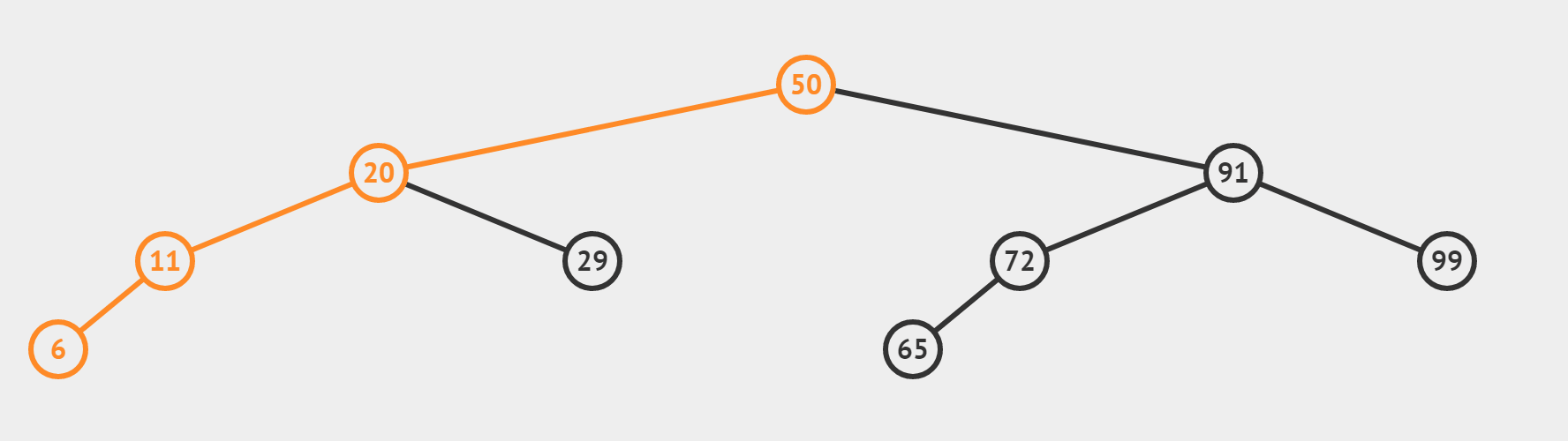
③中间位置取法的区别
以一组数据 [ 1, 2, 3, 4 , 5, 6 ]为🌰:
- mid = (left + right) / 2, 则获得的mid = (0 + 5) / 2 = 2
- mid = (left + right + 1) / 2, 则获得的mid = (0 + 5 + 1) / 2 = 3?
- 两种方法构造出的二叉树偏向不同,若某结点只有一个子结点,方法一得到的子节点一定是往右偏,方法二得到的一定是往左偏(如上图的 6 , 65 都是往左偏的)
?[小细节]
如果left + right 存在溢出的问题,则上述中间位置的取法可以改成下面两种形式,保证不会溢出
- (right - left) >> 1 + left
- (right?- left + 1) >> 1 + left?
④为什么称其为左闭右闭型
? ? ? ? 因为左闭右闭型检索的区域在? [left , right]? 之间。同样的道理,左闭右开检索的区域在 [left, right), 左开右闭的检索区域在 (left, right]
三、左开右闭,左闭右开型
①左闭右开,左开右闭,左闭右开的区分
? ? ? 核心在于while判断语句中有没有等于号,以及中间值的取法。试想left 与 right不断接近时,最终left 与right紧挨:
1)?中间值取法为 (left + right) / 2 时
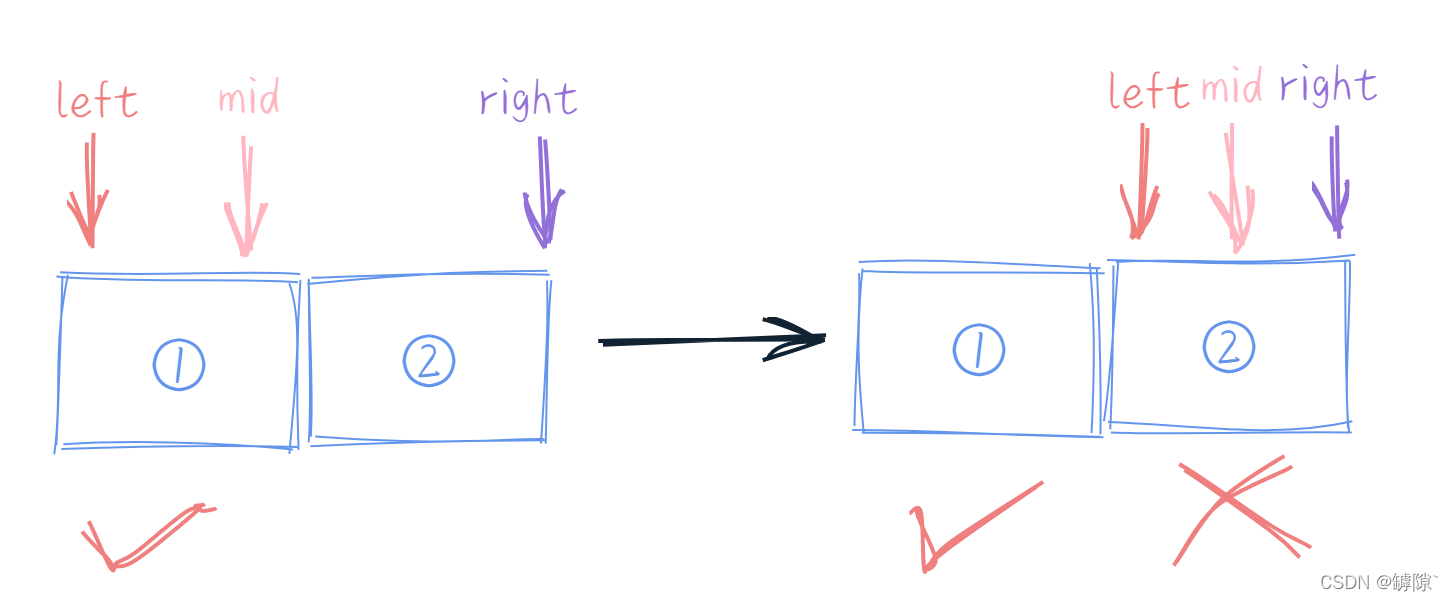
- ?若判断条件为 left <= right, 循环继续,则点②也会被判断,所以为左闭右闭
- ?若判断条件为 left < right, 循环结束, 则点②点不会被判断,只有点①被检索,所以称为左闭右开(如上图)
2)中间值取法为 (left + right + 1) / 2 时
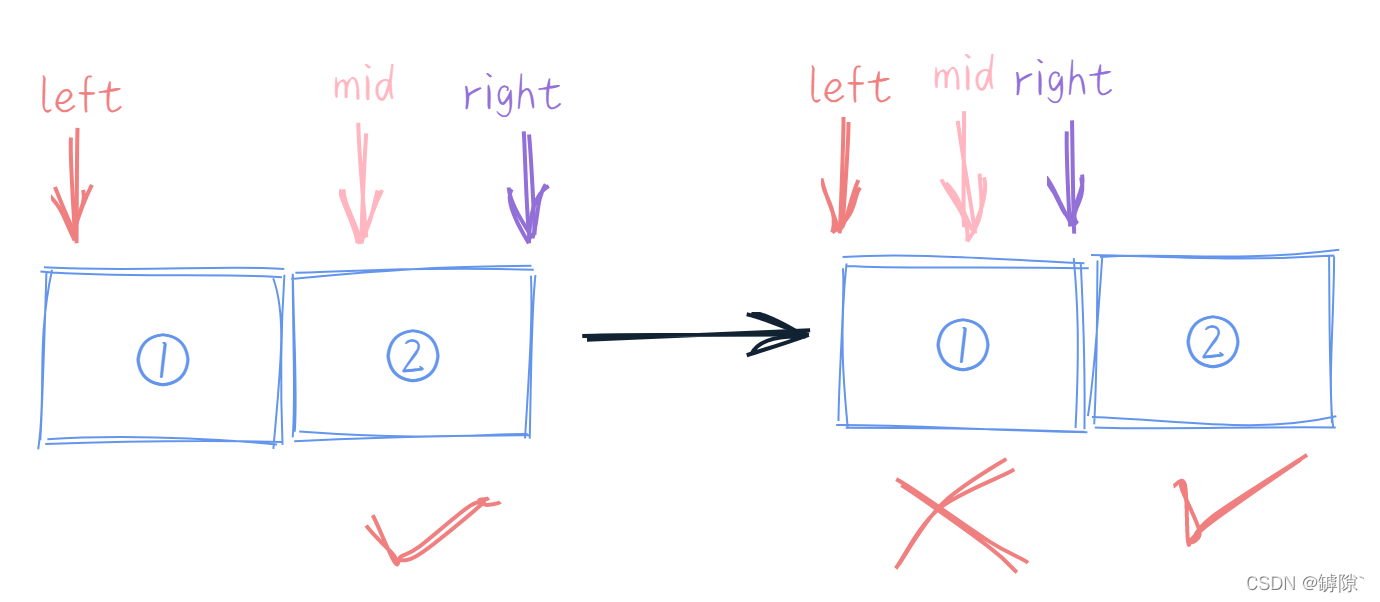
- ?若判断条件为 left <= right,则循环继续,则点①也会被检索,所以为左闭右闭
- 若判断条件为 left < = right,则循环结束,则点①点不会被检索,只有点②被检索,所以称为左开右闭(如上图)
四、寻找上下界
二分查找除了可以用来检索一个数是否存在,还可以用来寻找上下界,来看看是怎样实现的吧!
📃题目①:
假设你有n个版本[1, 2, ..., n],已知每个版本都是基于前一版本开发的。由于中间某一版本发生错误,导致之后的所有版本都是错误的。现需要你找出一个发生错误的版本。你可以调用函数bool isBadVersion(version)?来检测当前版本是否是错误版本(是错误版本返回1, 否则返回0)
int firstBadVersion(int n)
{
int left = 1;
int right = n;
while(left < right)
{
int mid = (right - left) / 2 + left;
if(isBadVersion(mid))
right = mid;
else
left = mid + 1;
}
return left;
}?【分析】
1)为什么想到二分查找?
? ? ? ? 因为二分查找的本质是二段性,只要满足二段性的问题都可以转化为二分查找的问题。
2)如何理解二段性呢?
? ? ? ? 在猜数字游戏中,二段性体现在target左边的元素都比它小,target右边的元素都比它大,所以结合数据的单调性我们可以不断的压缩区间以定位到目标值。而在这个问题中仍然具有二段性,第一个发生错误的版本的之前版本的都是正确的,之后的都是错误的,由此我们仍然可以不断的压缩区间从而得到第一个发生错误的版本。
3)如何理解左开右闭型的代码?
? ? ? ? 若当前mid版本为正确,则 left 可以压缩到mid + 1,若当前版本正确,则将right压缩到mid。可以是mid - 1吗?不妨这样思考,如果当前mid正处于第一个发生错误的版本,right = mid - 1后不是彻底排除了正确答案了吗,永远也找不到了。
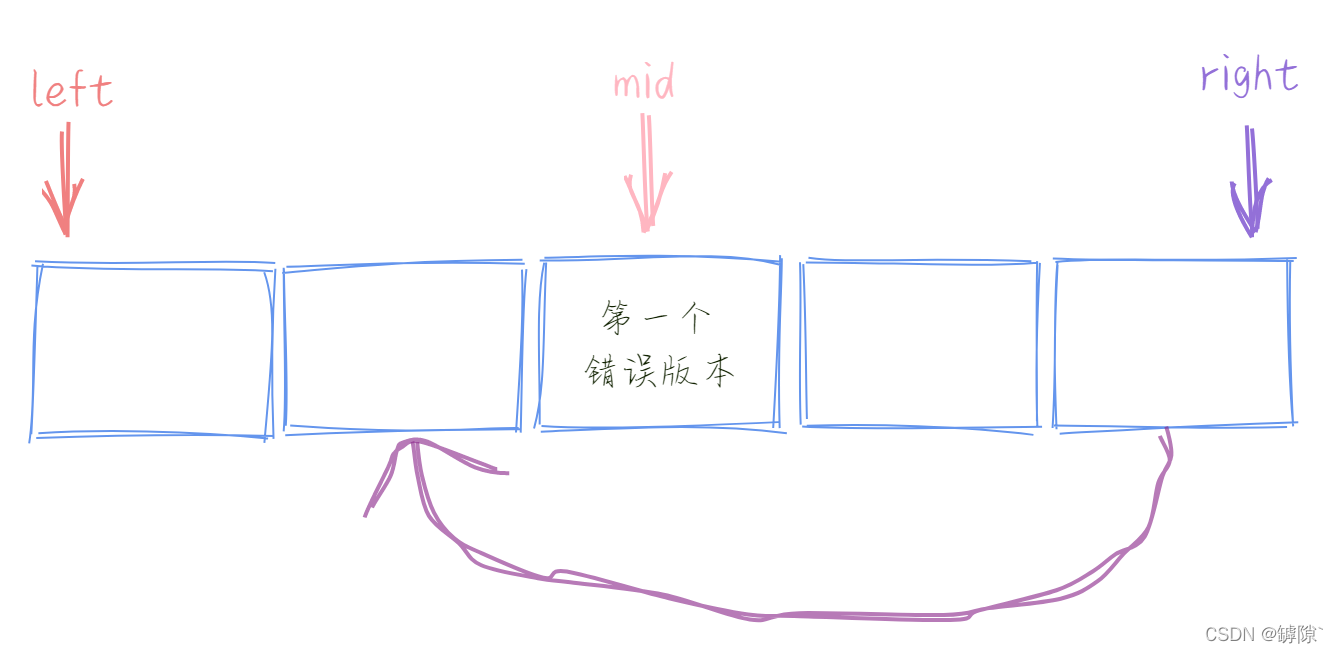
?????????left 和 right 相遇之前,left不可能到达第一个错误版本,只会无限接近;right不可能超过第一个错误版本,只会到达第一个错误版本,所以最后 left 与 right 的关系是这样的。最终,?left = mid + 1使得 left 与 right重合也就锁定了第一个错误版本 。
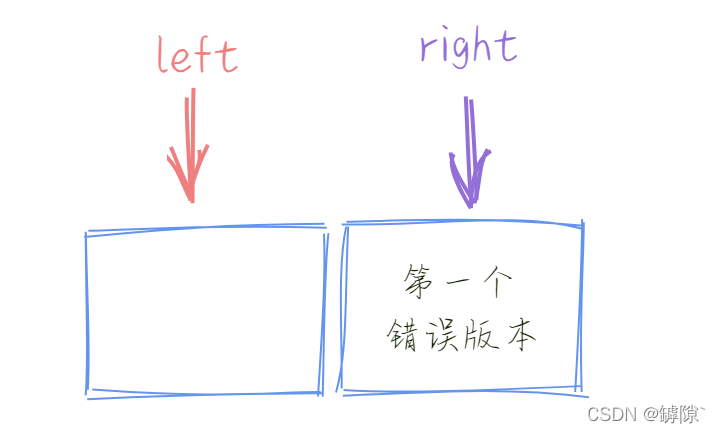
4)如果上体的中间元素取法为 (left + right + 1) / 2会发生什么?
? ? ? ? 会陷入死循环!?因为 mid = right,mid是错误版本,因此执行语句"right = mid",也就意味着left 与 right的区间没有发生压缩。不断重复这个过程就陷入了死循环。
5)延伸:如果最后的结果是这样的呢?
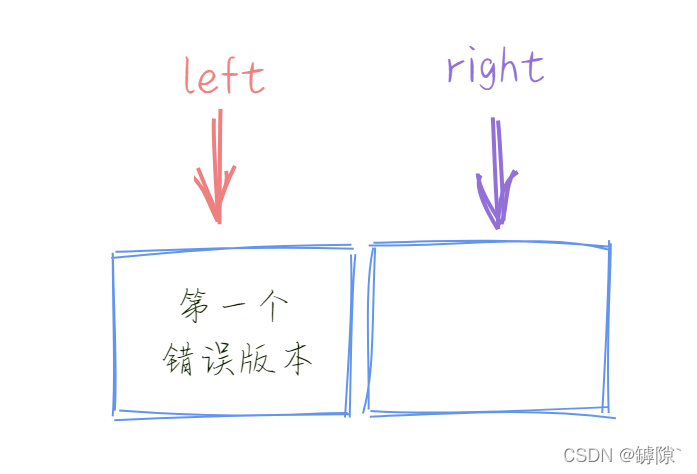
此时我们的中间元素取法如果为(left + right ) / 2 ,则同样的我们会陷入死循环。
6)总结
- 左闭右开型的只可以用来寻找下界,左开右闭型的只可以用来寻找上界
- 根据题意明确好需要寻找上界还是下界后,我们就确定了中间元素的取法。对left,right怎么处理呢?举个例子,左闭右开型的左边是取到到的,那么加1的任务一定要交给它,保证不会陷入死循环。
📃题目②:
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
用左闭右闭型的二分查找也可以实现上下界定位,并且好理解很多。来看看是怎么实现的:
int searchInsert(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1, ans = numsSize;
while (left <= right)
{
int mid = ((right - left) >> 1) + left;
if (target <= nums[mid])
{
ans = mid;
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return ans;
}
【分析】与模板唯一的区别在于,找到了继续找。所以上述代码的作用是找到第一个比target小的位置(也就是要插入位置)。当然如果将if里的条件改成 " target >= nums[mid] ",那么相应的作用就变成找到第一个闭target大的位置,当然也可以作为插入位置。
给大家演示一下: nums[] = {1, 2, 2, 2, 2, 2, 2, 3 ,4 ,5} , target? = 2 的情况吧?
?
?五、巩固练习
| 题目 | 地址 |
|---|---|
| 力扣地址 | |
| 力扣地址 | |
| 力扣地址 |
代码上面都呈现过,一定要都尝试下。