开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【初学线段树，看这篇文章准没错】线段树（单点修改and区间修改）acm寒假集训日记22/1/10 -> 正文阅读

[数据结构与算法]【初学线段树，看这篇文章准没错】线段树（单点修改and区间修改）acm寒假集训日记22/1/10

线段树

线段树是算法竞赛中常用的用来维护区间信息的数据结构。是一名ACMer 需要掌握的一种基础、重要的数据结构线段树可以在O(logN)的时间复杂度内实现单点修改，区间修改，区间查询（区间求和，区间最大值、最小值，区间gcd ）等操作

问题导入：

给你一个数组a , 有m次操作我们现在有 $4$ 种操作：

1. 询问【L,R】区间sum

2. 询问【L,R】区间max

3. 修改 a[pos] = new

4. 给区间【L,R】区间每一个数都加上 x

数组大小 1e5, m大小1e5

建树 build（二分的思想）

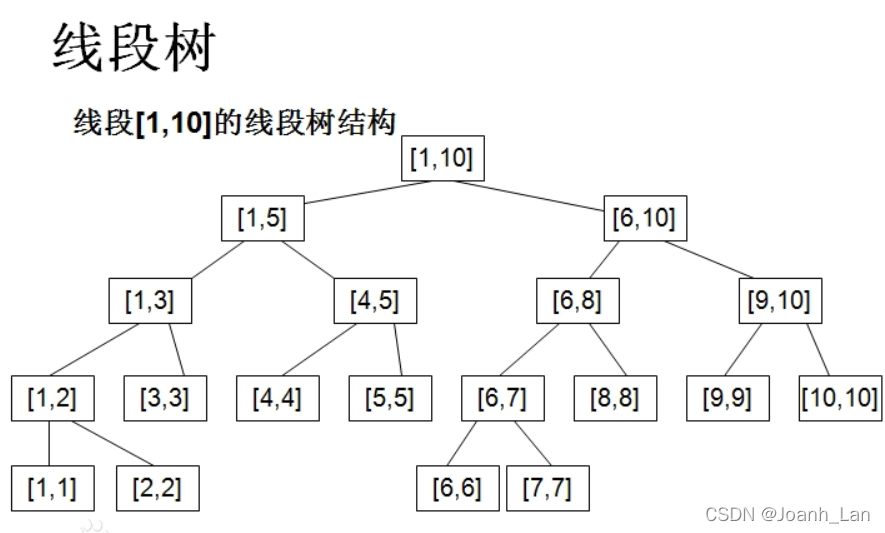
代码实现：

用结构体定义出抽象的树：

const int N = 5e4+5;
int a[N];
//树
struct Node
{
	int l,r;//区间 
	int sum;//区间和 
	int mid()//中间值 
	{
		return (l+r)/2;
	 } 
}tre[4*N]; //空间要开4倍！！！

build函数建树：

void build(int rt,int l,int r)
{
	if(l==r)
	{
		tre[rt] = {l,r,a[l]};
	}
	else
	{
		tre[rt] = {l,r};//将rt的区间赋值
		int mid = tre[rt].mid();
		//注意pushup一定要放最后！ 
		build(rt*2,l,mid);//递归左儿子
		build(rt*2+1,mid+1,r);//递归右儿子
		pushup(rt);//递归到终点，开始回溯，并由lson,rson更新父亲节点 
	}
	
}

pushup是回溯操作，下文介绍作用and代码实现

区间合并pushup函数（回溯）

请看下面图：

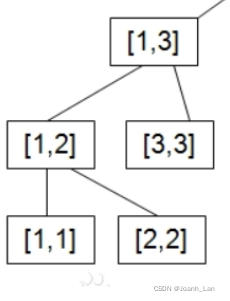
假设：

【1，1】-》1

【2，2】-》2

【3，3】-》3

（回溯的时候）【1，2】 = 【1，1】+【2，2】 = 3

???????????????????????? 【1，3】 = 【1，2】+【3，3】 = 6

规律：父亲的sum = 左儿子的sum+右儿子的sum

代码实现：

void pushup(int rt)//pushup操作更新父节点信息
{
	//左孩子+右孩子 
	tre[rt].sum = tre[rt*2].sum+tre[rt*2+1].sum;
}

区间查询 query

代码实现：

int query(int rt,int l,int r)
{
	//如果查询区间严格包含于我们要查找的区间[l,r]，直接return
	if(tre[rt].l>=l&&tre[rt].r<=r)
	return tre[rt].sum;
	else
	{
		int mid = tre[rt].mid();
		int ans = 0;
		//如果l<=当前节点mid,递归lson
		if(l<=mid) ans += query(rt*2,l,r);
		//如果r>=当前节点mid,递归rson
		if(r>mid) ans+=query(rt*2+1,l,r);
		return ans;
	}
}

单点修改 modify?

代码实现：

//修改modify (rt,x,pos) 将x节点加上pos
void modify(int rt,int x,int pos)
{
	if(tre[rt].l==x&&tre[rt].r==x)
	tre[rt].sum += pos;
	else
	{
		int mid = tre[rt].mid();
		//如果x在mid的左边,递归lson
		if(x<=mid) modify(rt*2,x,pos);
		//反之在右边,递归rson
		else modify(rt*2+1,x,pos);
		//不要忘了，更新完x也要向上更新父节点
		pushup(rt);	
	}
}

来一道例题试试手吧！

敌兵布阵（经典例题）

题目如下：

Lily特别喜欢养花，但是由于她的花特别多，所以照料这些花就变得不太容易。她把她的花依次排成一行，每盆花都有一个美观值。如果Lily把某盆花照料的好的话，这盆花的美观值就会上升，如果照料的不好的话，这盆花的美观值就会下降。有时，Lily想知道某段连续的花的美观值之和是多少，但是，Lily的算术不是很好，你能快速地告诉她结果吗?

第一行一个整数T，表示有T组测试数据。
每组测试数据的第一行为一个正整数N (N<=50000)，表示Lily有N盆花。
接下来有N个正整数，第i个正整数ai (1<=ai<=50) 表示第i盆花的初始美观值。
接下来每行有一条命令，命令有4种形式：
（1）Add i j, i和j为正整数，表示第i盆花被照料的好，美观值增加j (j<=30)
（2）Sub i j, i和j为正整数，表示第i盆花被照料的不好，美观值减少j (j<=30)
（3）Query i j, i和j为正整数，i<=j，表示询问第i盆花到第j盆花的美观值之和
（4）End，表示结束，这条命令在每组数据最后出现
每组数据的命令不超过40000条

对于第i组数据，首先输出"Case i:"和回车。
对于每个"Query i j"命令，输出第i盆花到第j盆花的美观值之和。

Sample Input

1
10
1 2 3 4 5 6 7 8 9 10
Query 1 3
Add 3 6
Query 2 7
Sub 10 2
Add 6 3
Query 3 10
End

Sample Output

Case 1:
6
33
59

AC代码如下：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int N = 5e4+5;
int a[N];
//树
struct Node
{
	int l,r;//区间 
	int sum;//区间和 
	int mid()//中间值 
	{
		return (l+r)/2;
	 } 
}tre[4*N]; //空间要开4倍！！！ 
void pushup(int rt)//pushup操作更新父节点信息
{
	//左孩子+右孩子 
	tre[rt].sum = tre[rt*2].sum+tre[rt*2+1].sum;
}
/*  
建树build (rt,l,r)
节点编号rt, 左端点l，右端点r
*/
void build(int rt,int l,int r)
{
	if(l==r)
	{
		tre[rt] = {l,r,a[l]};
	}
	else
	{
		tre[rt] = {l,r};//将rt的区间赋值
		int mid = tre[rt].mid();
		//注意pushup一定要放最后！ 
		build(rt*2,l,mid);//递归左儿子
		build(rt*2+1,mid+1,r);//递归右儿子
		pushup(rt);//递归到终点，开始回溯，并由lson,rson更新父亲节点 
	}
	
}
//查询 
int query(int rt,int l,int r)
{
	//如果查询区间严格包含于我们要查找的区间[l,r]，直接return
	if(tre[rt].l>=l&&tre[rt].r<=r)
	return tre[rt].sum;
	else
	{
		int mid = tre[rt].mid();
		int ans = 0;
		//如果l<=当前节点mid,递归lson
		if(l<=mid) ans += query(rt*2,l,r);
		//如果r>=当前节点mid,递归rson
		if(r>mid) ans+=query(rt*2+1,l,r);
		return ans;
	}
}
//修改modify (rt,x,pos) 将x节点加上pos
void modify(int rt,int x,int pos)
{
	if(tre[rt].l==x&&tre[rt].r==x)
	tre[rt].sum += pos;
	else
	{
		int mid = tre[rt].mid();
		//如果x在mid的左边,递归lson
		if(x<=mid) modify(rt*2,x,pos);
		//反之在右边,递归rson
		else modify(rt*2+1,x,pos);
		//不要忘了，更新完x也要向上更新父节点
		pushup(rt);	
	}
}

int main()
{
	int t;
	scanf("%d",&t);
	int cnt = 1;
	while(t--)
	{
		printf("Case %d:\n",cnt++);
		int n;
		scanf("%d",&n);
		for(int i = 1;i<=n;i++)
		scanf("%d",&a[i]);
		build(1,1,n);
		while(1)
		{
			char ch[10];
			int a,b;
			scanf("%s",ch);
			if(ch[0]=='E')
			break;
			scanf("%d %d",&a,&b); 
			if(ch[0]=='Q')
			printf("%d\n",query(1,a,b));
			else if(ch[0]=='A')
			modify(1,a,b);
			else
			modify(1,a,-b); 
		}
	 } 
	
	
 }

区间修改

想一下，如果使用单点修改去修改一个区间，加入让这个区间都加上一个pos一次单点修改是logn的复杂度，区间最大也就是【1，n】，那么一次区间修改的复杂度将达到nlog(n)的复杂度真是太难受了，还不如暴力for循环那为了解决这个问题，使用区间修改，可以帮助我们以logn的复杂度去完成区间修改

if(tre[rt].l>=l&&tre[rt].r<=r )
return tre[rt].sum

如果我们遇到一个完整的区间的话，并不需要继续往下走，直接在这里return即可，减少了许多分支，大大降低了时间复杂度那我们修改是不是同样的道理，如果我想给这一个完整的区间加上一个数的话，我只需要在此节点上打上一个标记lazy，下面的路我就不走了。什么时候走那，当开始问我被这个节点影响的子节点时，我是不是一定要把所有有关他父节点的lazy都加上，我会跟着query的方向，再把这个lazy下放，那么最后访问到的总和就是对的。这样我就实现了以O(logn)的复杂度完成了区间修改

引入新变量

在上面的基础上我们引入一个新的东西：lazy这个lazy表示的是我们对当前这个区间进行修改的量现在我们严格定义一下sum : sum代表当前区间总和。lazy : 懒标记，以当前节点rt为根的子树中的每一个节点都加上lazy这个数（强调一下，不包含根节点）

建树：

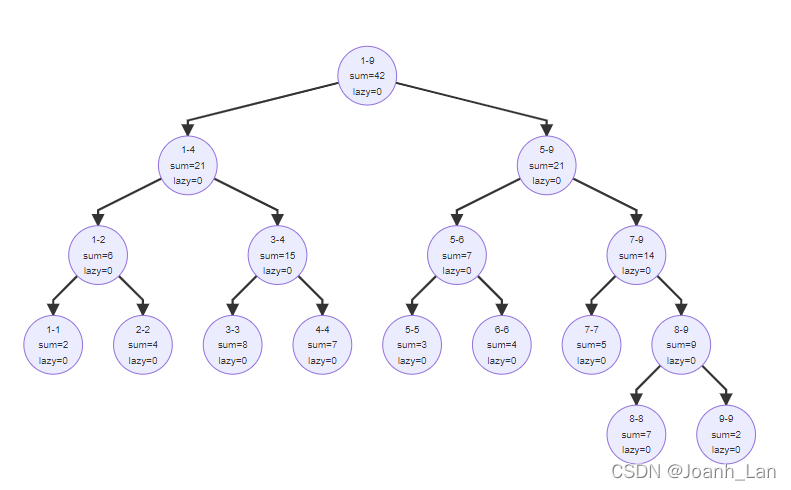
下放pushdown

?代码实现：

void pushdown(int rt)
{
	if(tre[rt].lazy)
	{
		tre[rt<<1].lazy+=tre[rt].lazy;// 把父节点rt的lazy传给左右儿子
		tre[rt<<1|1].lazy+=tre[rt].lazy;
		tre[rt<<1].sum+=(tre[rt<<1].r-tre[rt<<1].l+1)*tre[rt].lazy;// sum加上的值就是区间长度*父节点.lazy
		tre[rt<<1|1].sum+=(tre[rt<<1|1].r-tre[rt<<1|1].l+1)*tre[rt].lazy;
		tre[rt].lazy = 0;// 不要忘记清空lazy
	}
}

为什么我要不包含根节点那？

想一个问题，假如我第一次修改 3-4 上区间都加上10，紧接着我修改4-5上的区间都加上12如果之前我的lazy没有下放，是不是有个问题，我4这个节点到底是加上10 还是加上12，有冲突了吧。有冲突说明不对，如何解决这个冲突那？当我们访问到某个节点的时候，我们顺便也要把他的lazy给下放，让他们的儿子去交代清楚，不要把这个问题留给父亲

区间查询

代码实现：

ll query(int rt,int l,int r)
{
	if(tre[rt].l>=l&&tre[rt].r<=r)
	return tre[rt].sum;
	else
	{
		pushdown(rt);
		ll ans = 0;
		int mid = tre[rt].mid();
		if(l<=mid) ans+=query(rt<<1,l,r);
		if(r>mid) ans+=query(rt<<1|1,l,r);
		return ans;
	}
}

?还是来一道例题试试手！

题目如下：

A Simple Problem with Integers

队长给出了一个序列，想让你帮队长干活，你需要处理如下两种情况。

"C a b c"表示给[a, b]区间中的值全部增加c (-10000 ≤ c ≤ 10000)。

"Q a b" 询问[a, b]区间中所有值的和。

第一行包含两个整数N, Q。1 ≤ N,Q ≤ 100000.

第二行包含n个整数，表示初始的序列A (-1000000000 ≤ Ai ≤ 1000000000)。

接下来Q行询问，格式如题目描述。

对于每一个Q开头的询问，你需要输出相应的答案，每个答案一行。

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

AC代码如下：

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
const int N = 1e5+9;
ll a[N];
struct nn
{
	int l,r;
	ll sum;
	ll lazy;
	int mid()
	{
		return l+r>>1;
	}
}tre[4*N];
void pushup(int rt)
{
	tre[rt].sum = tre[rt<<1].sum+tre[rt<<1|1].sum;
}
void pushdown(int rt)
{
	if(tre[rt].lazy)
	{
		tre[rt<<1].lazy+=tre[rt].lazy;
		tre[rt<<1|1].lazy+=tre[rt].lazy;
		tre[rt<<1].sum+=(tre[rt<<1].r-tre[rt<<1].l+1)*tre[rt].lazy;
		tre[rt<<1|1].sum+=(tre[rt<<1|1].r-tre[rt<<1|1].l+1)*tre[rt].lazy;
		tre[rt].lazy = 0;
	}
}
void build(int rt,int l,int r)
{
	if(l==r)
	tre[rt] = {l,r,a[l],0};
	else
	{
		tre[rt] = {l,r};
		int mid = tre[rt].mid();
		build(rt<<1,l,mid);
		build(rt<<1|1,mid+1,r);
		pushup(rt);
	}
}
ll query(int rt,int l,int r)
{
	if(tre[rt].l>=l&&tre[rt].r<=r)
	return tre[rt].sum;
	else
	{
		pushdown(rt);
		ll ans = 0;
		int mid = tre[rt].mid();
		if(l<=mid) ans+=query(rt<<1,l,r);
		if(r>mid) ans+=query(rt<<1|1,l,r);
		return ans;
	}
}
void modify(int rt,int l,int r,ll v)
{
	if(tre[rt].l>=l&&tre[rt].r<=r)
	{
		tre[rt].lazy+=v;
		tre[rt].sum+=(tre[rt].r-tre[rt].l+1)*v;
	}
	else
	{
		pushdown(rt);
		int mid = tre[rt].mid();
		if(l<=mid) modify(rt<<1,l,r,v);
		if(r>mid) modify(rt<<1|1,l,r,v);
		pushup(rt);
	}
}
int main()
{
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i = 1;i<=n;i++)
	scanf("%lld",&a[i]);
	build(1,1,n);
	while(m--)
	{
		int l,r;
		ll v;
		char ch[10];
		scanf("%s %d %d",ch,&l,&r);
		if(ch[0]=='Q')
		printf("%lld\n",query(1,l,r));
		else
		{
			scanf("%lld",&v);
			modify(1,l,r,v);
		}
	}
 }

区间最大值

其实只需要在上面所学的基础上修改一下就可以了

查询query

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;//整个数的中点
    int maxv = -1;
    if (l <= mid)maxv = query(u << 1, l, r);
    if (r > mid)maxv = max(maxv, query(u << 1 | 1, l, r));
    //pushup(u);
    return maxv;
}

区间合并pushup

void pushup(int u)
{
    tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
}

?还是，还是，还是来看一道例题！

题目如下：

数列区间最大值

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

第一行两个整数 N,M 表示数字的个数和要询问的次数；
接下来一行为 N 个数；
接下来 M 行，每行都有两个整数 X,Y。

输出共 M 行，每行输出一个数。

样例
Input Output
10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8
5
8
数据范围与提示

对于全部数据，1≤N≤1e5,1≤M≤1e6,1≤X≤Y≤N。数字不超过 C/C++ 的 int 范围。

AC代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <climits>

using namespace std;

const int N = 100010;

int n, m;
int w[N];
struct Node
{
    int l, r;
    int maxv;
}tr[N * 4];

void pushup(int u)
{
    tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
}

void build(int u, int l, int r)
{
    if (l == r)tr[u] = { l,r,w[l] };
    else {
        tr[u] = { l, r };//赋值
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r)return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;//整个数的中点
    int maxv = -1;
    if (l <= mid)maxv = query(u << 1, l, r);
    if (r > mid)maxv = max(maxv, query(u << 1 | 1, l, r));
    //pushup(u);
    return maxv;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) scanf("%d", &w[i]);

    build(1, 1, n);

    int a, b;
    while (m--)
    {
        scanf("%d%d", &a, &b);
        printf("%d\n", query(1, a, b));
    }

    return 0;
}