开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 算法学习——剑指 Offer II 039. 直方图最大矩形面积（Java实现蛮力，分治，单调栈） -> 正文阅读

[数据结构与算法]算法学习——剑指 Offer II 039. 直方图最大矩形面积（Java实现蛮力，分治，单调栈）

文章目录

1. 题意

1. 题意

给定非负整数数组 heights ，数组中的数字用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

这是LeetCode上的 [039，直方图最大矩形面积]，难度为 [困难]

2. 思路分析

要想求直方图的最大矩型面积，可以求出所有柱子的组合情况，面积最大的柱子组合而得矩形就是最大矩形面积，因此需要知道直方图中柱子组合而成的矩形的宽和高。

例如直方图中组合柱子矩形从下标为i的柱子的开始，到下标为j的柱子结束，那么这个矩形的宽度就是j - i + 1（下标从0开始)，矩形高度为两个柱子之间的所有柱子最矮的高度

3. 蛮力法

3.1 题解

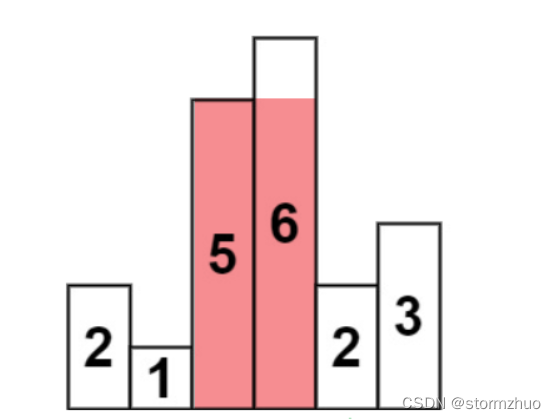
蛮力法得解法比较直观，我们可以使用嵌套循环遍历柱子数组，遍历过程中让当前柱子与当前柱子后面的每一个柱子组合成矩形，然后比较它们的面积，宽即为遍历过程中当前柱子后面的某个柱子的下标减去当前柱子的下标加1（下标从0开始)，高为遍历过程中柱子高度最矮的那个，如下图所示

在这里插入图片描述

3.2 代码实现

 public int largestRectangleArea(int [] heights) {
        // 记录最大矩形面积
        int maxArea = 0;
        /* 遍历数组，遍历过程中让当前柱子与当前柱子后面的每一个柱子组合成矩形
        *  并算出面积以求出最大矩形面积*/
        for (int i = 0; i < heights.length; i++) {
            // 记录遍历过程最矮的柱子
            int minHeight = heights[i];
            for (int j = i; j < heights.length; j++) {
                minHeight = Math.min(minHeight, heights[j]);
                int area = minHeight * (j - i + 1);
                maxArea = Math.max(maxArea, area);
            }
        }
        return maxArea;
    }

3.2 复杂度分析

假设输入的数组长度为n

时间复杂度

需要嵌套遍历直方图，故时间复杂度为O(n²)

空间复杂度

除了声明几个变量，没有其他额外的内存开销，故空间复杂度为O(1)

4. 分治法

4.1 题解

分治法的思想可以通俗的解释为：把一片领土分解，分解为若干块小部分，然后一块块地占领征服，被分解的可以是不同的政治派别或是其他什么，然后让他们彼此异化。

回归到题意，可以使用分治法思想可以把求直方图的最大矩形分解为3种可能。

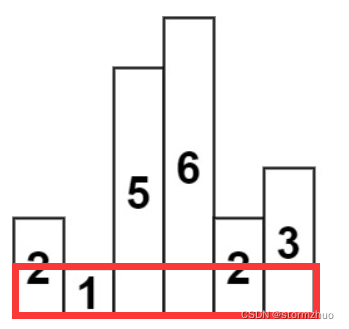
第1种是最大矩形通过最矮的柱子求得最大面积，即最大矩形的高度为最矮柱子的高度，长度为直方图的长度，如下所示

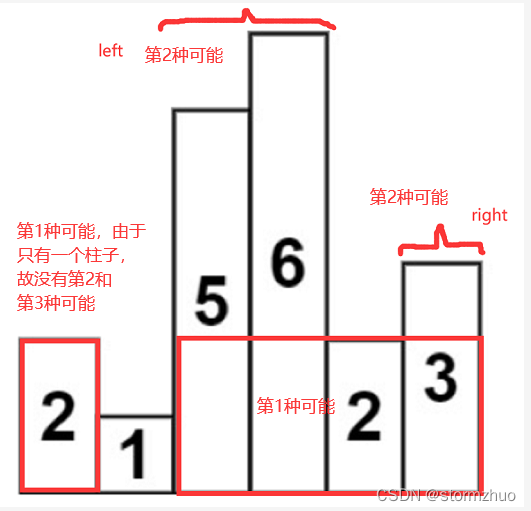
在这里插入图片描述

第2种可能是最大矩形的起始柱子和终止柱子都在最矮的柱子的左侧

第3种可能是最大矩形的起始柱子和终止柱子都在最矮的柱子的右侧

很显然，第2种和第3种可能从本质上来说也是和求整个直方图的最大矩形面积是同一个问题，即它们又把求直方图的最大矩形分解为3种可能，因此可以调用递归函数来解决，直至到达递归出口，即有返回值，如下所示

在这里插入图片描述

递归出口分为两种情况

最矮柱子为起始柱子或终止柱子，此时最矮柱子左边或右边没有柱子，故最矮柱子的左边或右边的最大矩形面积都可认为是0
最矮柱子左边或右边只有一个柱子，此时按第一种可能算面积

当到达递归出口时，递归返回，比较三种可能的最大面积，最大的即为直方图的最大矩形面积

4.2 代码实现

class Solution {
    public int largestRectangleArea(int [] heights) {
        return helper(heights, 0, heights.length);
    }

    private int helper(int[] heights, int start, int end) {
     /* 递归出口
        最矮柱子是起始柱子，则最矮柱子左边的最大矩形面积为0
        最矮柱子是终止柱子，则最矮柱子右边的最大矩形面积为0*/
        if (start == end) {
            return 0;
        }
        // 递归出口，最矮柱子左边或后边只有一个柱子
        if (start + 1 == end) {
            return heights[start];
        }
        // 记录最矮柱子的下标，初始为起始柱子
        int minIndex = start;
        // 在起始柱子和终止柱子之间找到最矮柱子
        for (int i = start + 1; i  < end; i ++) {
            if (heights[i] < heights[minIndex]) {
                minIndex = i;
            }
        }
        // 第一种可能的最大矩形面积
        int shortArea = (end - start) * heights[minIndex];
        // 第二种可能的最大矩形面积，调用递归，又可能分解为三种可能
        int leftArea = helper(heights, start, minIndex);
        // 第三种可能的最大矩形面积，调用递归，又可能分解为三种可能
        int rightArea = helper(heights, minIndex + 1, end);
        // 比较三种可能的面积算出最大面积
        int area = Math.max(shortArea, leftArea);
        return Math.max(area, rightArea);
    }
}

4.3 复制度分析

假设输入数组的长度为n

时间复杂度

如果每次都能将n根柱子分解成左右柱子数量都为n/2的子直方图，那么递归的深度为O(logn),可以理解为二分查找的复杂度

由于每次分解时都需要找到最矮的柱子，时间复杂度为O(n)

故总的时间复杂度为O(nlogn)

特别地，若直方图中的柱子的高度是排序的(递增或递减)，那么每次最矮的柱子都位于直方图的一侧，此时分解的柱子只有左边或右边的一种情况，时间复杂度为O(n)

由于每次分解时都需要找到最矮的柱子，时间复杂度为O(n)

故总的时间复杂度为O(n²)

空间复杂度

基于递归的分治法需要消耗内存来保存递归调用栈，故空间复杂度为O(logn)

最坏情况下，即直方图中的柱子的高度是排序的，空间复杂度为O(n)

5. 单调栈法

5.1 题解

单调栈顾名思义就是用栈来保存的数是单调有序的。这种解法的基本思想是确保保存在栈的直方图的柱子的高度是递增排序的，为了方便计算矩形的宽度，栈中保存的是柱子的下标，可以根据下标得出柱子的高度

遍历数组，遍历过程中如果当前柱子的高度大于栈顶的柱子高度，则把此柱子的下标入栈，否则栈顶柱子出栈，并计算栈顶柱子的最大矩形面积

那么如何确定出栈的栈顶柱子的最大矩形面积呢？该矩形的宽度一定是从栈顶柱子向两侧延申直到遇到比它矮的柱子之间的间隔

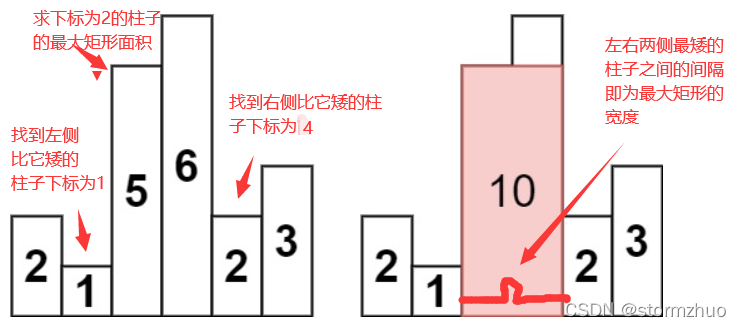
例如求下图所示的直方图中以下标为2的柱子应该从柱子开始向两侧延申，左侧比它矮的柱子的下标为1（高度为1)，右侧比它矮的柱子的下标为4(高度为2)，因此下标为2的柱子为顶的最大矩形面积的高为5，宽为2（左右侧比它矮的柱子的下标之差再减1)

在这里插入图片描述

特别地

若出栈的栈顶柱子是栈的唯一元素，则说明出栈的栈顶柱子左侧没有柱子，这意味着它的左侧的柱子都比它高，因此可以想象在下标为-1的位置有一根比它矮的柱子

当遍历完数组后，栈中可能仍然剩余一些柱子，因此，需要逐一将这些柱子的下标出栈并计算以它们为顶的最大矩形面积。

柱子直到这个时候才出栈，这说明它的右侧没有比它矮的柱子，因此想象成以当前出栈柱子为顶的最大矩形的下标往右一直延申到下标为数组的长度（数组长度为柱子的数量)

下面以 [2, 1, 5, 6, 2, 3] 为例说明，过程如图所示。

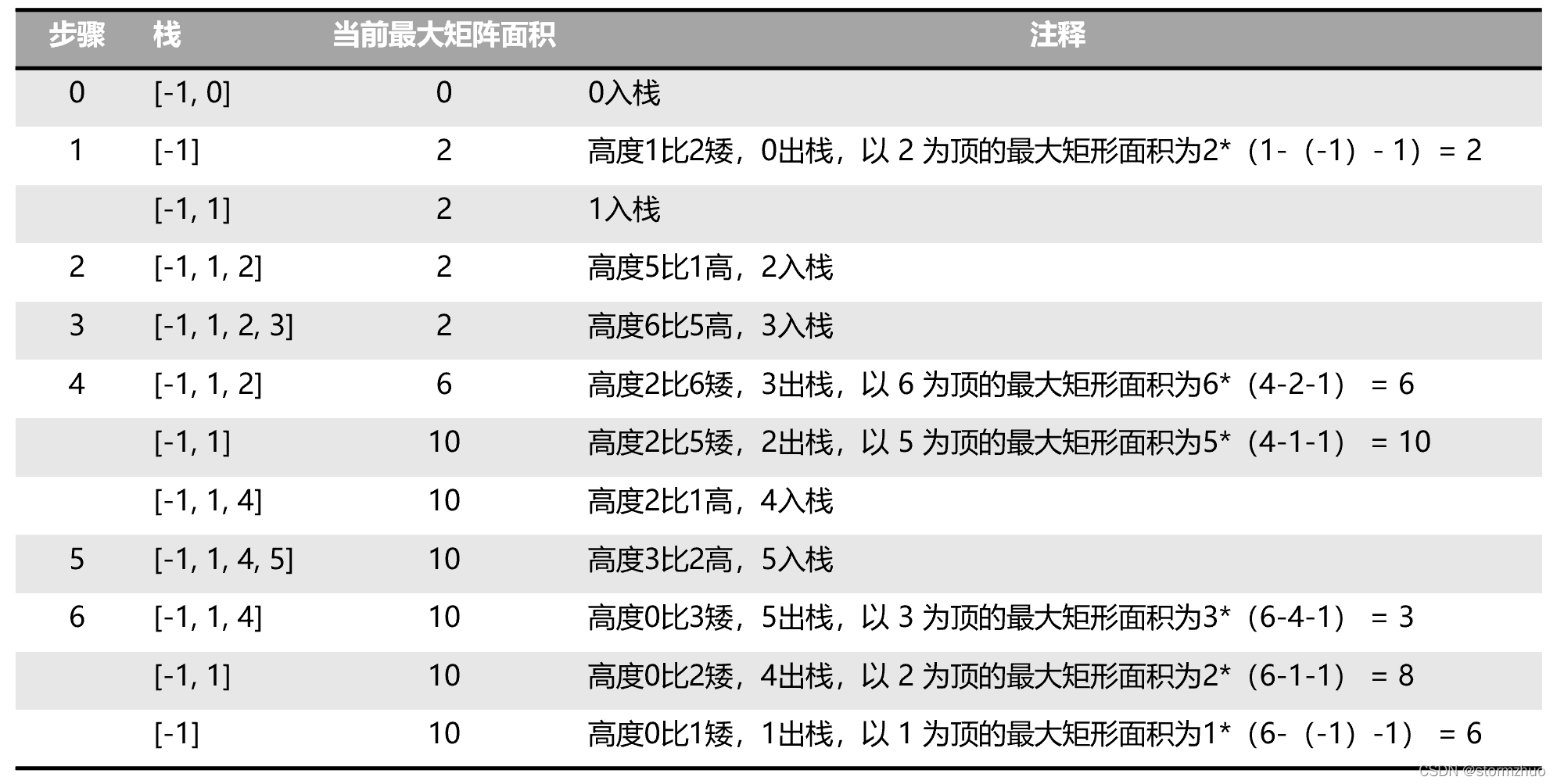
在这里插入图片描述

5.2 代码实现

class Solution {
    public int largestRectangleArea(int[] heights) {
       // 创建一个栈存放递增的柱子
        Deque<Integer> stack = new LinkedList<>();
        // 压入一个-1的下标，用来处理栈顶左侧没有柱子的情况
        stack.push(-1);
        // 记录最大矩形面积
        int maxArea = 0;
        // 遍历数组
        for (int i = 0; i < heights.length; i++) {
            // 若栈有柱子元素(-1是想象虚拟的柱子)，并且栈顶元素大于当前遍历的柱子高度执行逻辑
            while (stack.peek() != -1 && heights[stack.peek()] >= heights[i]) {
                // 弹出栈顶元素，计算栈顶元素的最大矩形面积
                int height = heights[stack.pop()];
                int width = i - stack.peek() - 1;
                maxArea = Math.max(height * width, maxArea);
            }
            stack.push(i);
        }
        // 遍历完数组后，栈可能还有柱子的执行逻辑
        while (stack.peek() != -1) {
            int height = heights[stack.pop()];
            int width = heights.length - stack.peek() - 1;
            maxArea = Math.max(height * width, maxArea);
        }
        return maxArea;
    }
}