海伦公式的推导
今天不知怎么的,想起了自己高一时候曾经证明出三角形的面积公式之一——海伦公式,受到老师的表扬,还高兴好一会儿。想要去找找当年的草稿纸,找了许久,不见踪迹,而记忆中的画面与置身其中的感觉越发清晰,同时又有些许失落。就好像你曾经干过惊天动地的事情,你也确定那是真实的,但现在却找不到任何的证据。
于是有感而发,循着丝丝模糊的记忆碎片,尝试将证明过程再写了下来:
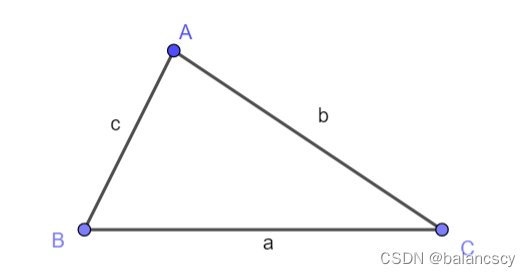
在
三
角
形
Δ
A
B
C
中
,
设
角
A
,
B
,
C
的
对
边
分
别
为
a
,
b
,
c
?
,
?
则
三
角
形
Δ
A
B
C
的
面
积
为
:
S
Δ
A
B
C
2
=
(
1
2
b
c
sin
?
A
)
2
=
1
4
b
2
c
2
(
1
?
cos
?
2
A
)
=
1
4
b
2
c
2
[
1
?
(
b
2
+
c
2
?
a
2
2
b
c
)
2
]
=
1
16
[
4
b
2
c
2
?
(
b
2
+
c
2
?
a
2
)
2
]
=
1
16
[
(
2
b
c
)
2
?
(
b
2
+
c
2
?
a
2
)
2
]
=
平
方
差
公
式
1
16
[
(
2
b
c
+
b
2
+
c
2
?
a
2
)
?
(
2
b
c
?
b
2
?
c
2
+
a
2
)
]
=
完
全
平
方
公
式
1
16
{
[
(
b
+
c
)
2
?
a
2
]
?
[
a
2
?
(
b
?
c
)
2
]
}
=
平
方
差
公
式
1
16
{
[
(
b
+
c
+
a
)
?
(
b
+
c
?
a
)
]
?
[
(
a
+
b
?
c
)
?
(
a
?
b
+
c
)
]
}
=
a
+
b
+
c
2
?
a
+
b
?
c
2
?
b
+
c
?
a
2
?
c
+
a
?
b
2
=
s
(
s
?
a
)
(
s
?
b
)
(
s
?
c
)
?
,
?
其
中
s
=
a
+
b
+
c
2
故
??
S
Δ
A
B
C
=
s
(
s
?
a
)
(
s
?
b
)
(
s
?
c
)
?
,
?
其
中
s
=
a
+
b
+
c
2
?
。
?
在三角形\Delta ABC中,设角A,B,C的对边分别为a,b,c\,,\, 则三角形\Delta ABC 的面积为: \\ \begin{aligned} S^2_{\Delta ABC} & =({1 \over 2}bc\sin{A})^2\\ & = {1 \over 4}b^2c^2 (1-\cos^2{A}) \\ &= {1 \over 4}b^2c^2 [1- ({b^2+c^2-a^2 \over 2bc})^2] \\ &= {1 \over 16}[4b^2c^2- (b^2+c^2-a^2)^2] \\ &= {1 \over 16}[(2bc)^2 - (b^2+c^2-a^2)^2] \\ & \xlongequal[]{平方差公式} {1 \over 16}[(2bc+b^2+c^2-a^2) \cdot (2bc-b^2-c^2+a^2)] \\ & \xlongequal[]{完全平方公式} {1 \over 16}\{[(b+c)^2-a^2] \cdot [a^2-(b-c)^2]\} \\ & \xlongequal[]{平方差公式} {1 \over 16}\{[(b+c+a) \cdot (b+c-a)] \cdot [(a+b-c) \cdot (a-b+c)]\} \\ &= {a+b+c \over 2} \cdot {a+b-c \over 2} \cdot {b+c-a \over 2} \cdot {c+a-b \over 2} \\ &= s(s-a)(s-b)(s-c)\,,\,其中 s = {a+b+c \over 2} \\ & 故\,\, S_{\Delta ABC} = \sqrt[]{s(s-a)(s-b)(s-c)}\,,\,其中 s = {a+b+c \over 2}\,。\, \end{aligned}
在三角形ΔABC中,设角A,B,C的对边分别为a,b,c,则三角形ΔABC的面积为:SΔABC2??=(21?bcsinA)2=41?b2c2(1?cos2A)=41?b2c2[1?(2bcb2+c2?a2?)2]=161?[4b2c2?(b2+c2?a2)2]=161?[(2bc)2?(b2+c2?a2)2]平方差公式?161?[(2bc+b2+c2?a2)?(2bc?b2?c2+a2)]完全平方公式?161?{[(b+c)2?a2]?[a2?(b?c)2]}平方差公式?161?{[(b+c+a)?(b+c?a)]?[(a+b?c)?(a?b+c)]}=2a+b+c??2a+b?c??2b+c?a??2c+a?b?=s(s?a)(s?b)(s?c),其中s=2a+b+c?故SΔABC?=s(s?a)(s?b)(s?c)?,其中s=2a+b+c?。?
嗯,好像就是这样
圆内接四边形的面积公式
在海伦公式的启发下,根据圆内接四边形对角互补(即对角相加为180
ο
?
^{\operatorname \omicron}
ο),稀里糊涂地又得到以下结论:
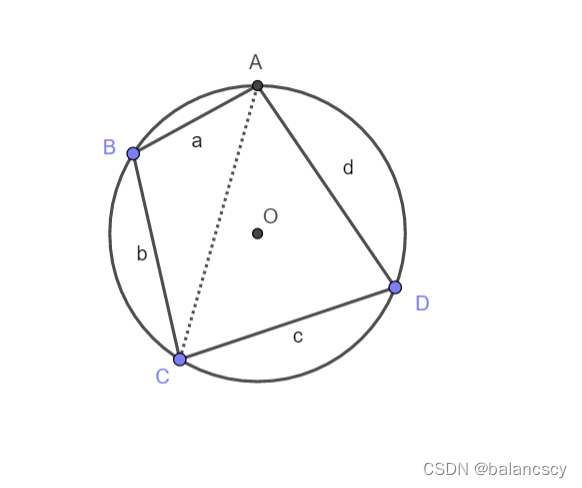
如
上
图
所
示
,
在
圆
O
中
有
内
接
四
边
形
A
B
C
D
,
A
B
边
记
为
a
,
B
C
边
记
为
b
,
C
D
边
记
为
c
,
D
A
边
记
为
d
设
A
C
连
线
为
t
?
,
?
则
四
边
形
A
B
C
D
的
面
积
为
:
S
=
1
2
a
b
sin
?
B
+
1
2
c
d
sin
?
D
=
B
+
D
=
2
π
1
2
(
a
b
+
c
d
)
sin
?
B
得
:
S
2
=
1
4
(
a
b
+
c
d
)
2
(
1
?
cos
?
2
B
)
=
1
4
(
a
b
+
c
d
)
2
(
1
+
cos
?
B
)
(
1
?
cos
?
B
)
(
1
)
由
于
B
+
D
=
2
π
,
则
cos
?
B
=
?
cos
?
D
则
有
:
a
2
+
b
2
?
t
2
2
a
b
=
?
c
2
+
d
2
?
t
2
2
c
d
整
理
可
得
:
t
2
=
2
a
b
c
d
a
b
+
c
d
(
a
2
+
b
2
2
a
b
+
c
2
+
d
2
2
c
d
)
(
2
)
将
(
2
)
式
代
入
cos
?
B
=
a
2
+
b
2
?
t
2
2
a
b
中
,
得
:
cos
?
B
=
1
2
(
a
b
+
c
d
)
?
[
(
a
2
+
b
2
)
?
(
c
2
+
d
2
)
]
于
是
:
1
+
cos
?
B
=
1
2
(
a
b
+
c
d
)
?
[
(
a
+
b
)
2
?
(
c
?
d
)
2
]
=
1
2
(
a
b
+
c
d
)
?
[
(
a
+
b
+
c
?
d
)
?
(
a
+
b
?
c
+
d
)
]
(
3
)
1
?
cos
?
B
=
1
2
(
a
b
+
c
d
)
?
[
(
c
+
d
)
2
?
(
a
?
b
)
2
]
=
1
2
(
a
b
+
c
d
)
?
[
(
c
+
d
+
a
?
b
)
?
(
c
+
d
?
a
+
b
)
]
(
4
)
将
(
3
)
与
(
4
)
代
入
(
1
)
中
,
得
:
S
2
=
(
a
+
b
+
c
?
d
2
)
?
(
b
+
c
+
d
?
a
2
)
?
(
c
+
d
+
a
?
b
2
)
?
(
d
+
a
+
b
?
c
2
)
如
果
设
?
ρ
=
a
+
b
+
c
+
d
2
?
,
?
则
:
S
2
=
(
ρ
?
a
)
(
ρ
?
b
)
(
ρ
?
c
)
(
ρ
?
d
)
于
是
:
S
=
(
ρ
?
a
)
(
ρ
?
b
)
(
ρ
?
c
)
(
ρ
?
d
)
?
,
?
ρ
=
a
+
b
+
c
+
d
2
?
。
?
%\usepackage{unicode-math} 如上图所示,在圆O中有内接四边形ABCD,\\ AB边记为a,BC边记为b,CD边记为c,DA边记为d \\ 设AC连线为t\,,\, 则四边形ABCD的面积为:\\ \begin{aligned} S &={1 \over 2}ab\sin{B}+{1 \over 2}cd\sin{D} \\ & \xlongequal[]{B+D=2\pi}{1 \over 2}(ab+cd)\sin{B} \\ 得:& S^2 = {1 \over 4}(ab+cd)^2(1-\cos^2B) \\ & = {1 \over 4}(ab+cd)^2(1+\cos{B})(1-\cos{B}) \quad (1) \end{aligned} \\ \begin{aligned} & 由于B+D=2\pi,则\cos{B}=-\cos{D} \\ & 则有:{a^2+b^2-t^2 \over 2ab} = -{c^2+d^2-t^2 \over 2cd}\\ & 整理可得:t^2 = {2abcd \over ab+cd}({a^2+b^2 \over 2ab}+{c^2+d^2 \over 2cd}) \quad (2)\\ & 将(2)式代入\cos{B}={a^2+b^2-t^2 \over 2ab}中,得:\cos{B}={1 \over 2(ab+cd)} \cdot [ (a^2+b^2) - (c^2+d^2) ] \\ 于是:& 1+\cos{B} = {1 \over 2(ab+cd)} \cdot [ (a+b)^2 - (c-d)^2 ] = {1 \over 2(ab+cd)} \cdot [ (a+b+c-d)\cdot (a+b-c+d) ]\quad (3) \\ & 1-\cos{B} = {1 \over 2(ab+cd)} \cdot [ (c+d)^2 - (a-b)^2 ] = {1 \over 2(ab+cd)} \cdot [ (c+d+a-b) \cdot (c+d-a+b) ]\quad (4) \\ & 将(3)与(4)代入(1)中,得:\\ S^2 &= ({a+b+c-d \over 2}) \cdot ({b+c+d-a \over 2}) \cdot ({c+d+a-b \over 2}) \cdot ({d+a+b-c \over 2}) \\ 如果设\, & \rho={a+b+c+d \over 2}\,,\,则 :\\ & S^2 = (\rho-a)(\rho-b)(\rho-c)(\rho-d) \\ 于是:& S = \sqrt[]{(\rho-a)(\rho-b)(\rho-c)(\rho-d)}\,,\,\rho={a+b+c+d \over 2}\,。\, \end{aligned}
如上图所示,在圆O中有内接四边形ABCD,AB边记为a,BC边记为b,CD边记为c,DA边记为d设AC连线为t,则四边形ABCD的面积为:S得:?=21?absinB+21?cdsinDB+D=2π?21?(ab+cd)sinBS2=41?(ab+cd)2(1?cos2B)=41?(ab+cd)2(1+cosB)(1?cosB)(1)?于是:S2如果设于是:?由于B+D=2π,则cosB=?cosD则有:2aba2+b2?t2?=?2cdc2+d2?t2?整理可得:t2=ab+cd2abcd?(2aba2+b2?+2cdc2+d2?)(2)将(2)式代入cosB=2aba2+b2?t2?中,得:cosB=2(ab+cd)1??[(a2+b2)?(c2+d2)]1+cosB=2(ab+cd)1??[(a+b)2?(c?d)2]=2(ab+cd)1??[(a+b+c?d)?(a+b?c+d)](3)1?cosB=2(ab+cd)1??[(c+d)2?(a?b)2]=2(ab+cd)1??[(c+d+a?b)?(c+d?a+b)](4)将(3)与(4)代入(1)中,得:=(2a+b+c?d?)?(2b+c+d?a?)?(2c+d+a?b?)?(2d+a+b?c?)ρ=2a+b+c+d?,则:S2=(ρ?a)(ρ?b)(ρ?c)(ρ?d)S=(ρ?a)(ρ?b)(ρ?c)(ρ?d)?,ρ=2a+b+c+d?。?
后来有了网,查找了一些资料,这原来是婆罗摩笈多公式,于是不禁肃然起敬,古代人们的智慧真是浩瀚如海,这些公式早就有了!
End
写到这竟然有些欣然惬意的快乐,哈哈,我也曾独立推导过一些数学公式,虽然前人之述备矣。继续加油!