DFS的学习
DFS的理解就像人处在一个迷宫中一样,需要靠自己一步步地去走,但是,DFS更像是一种走出迷宫的方法,我们在走迷宫的时候可以一直贴着右边的墙壁走,虽然碰到死路会一条路走到底,但是仔细想想,这种方法是可行的,因为我们还能贴着墙走出来,一但发现是死路可以贴着右墙原路返回到最初的岔路口,再选择其他的岔路走下去,虽然看上去荒谬,但是实际上是十分可行的。
例如:
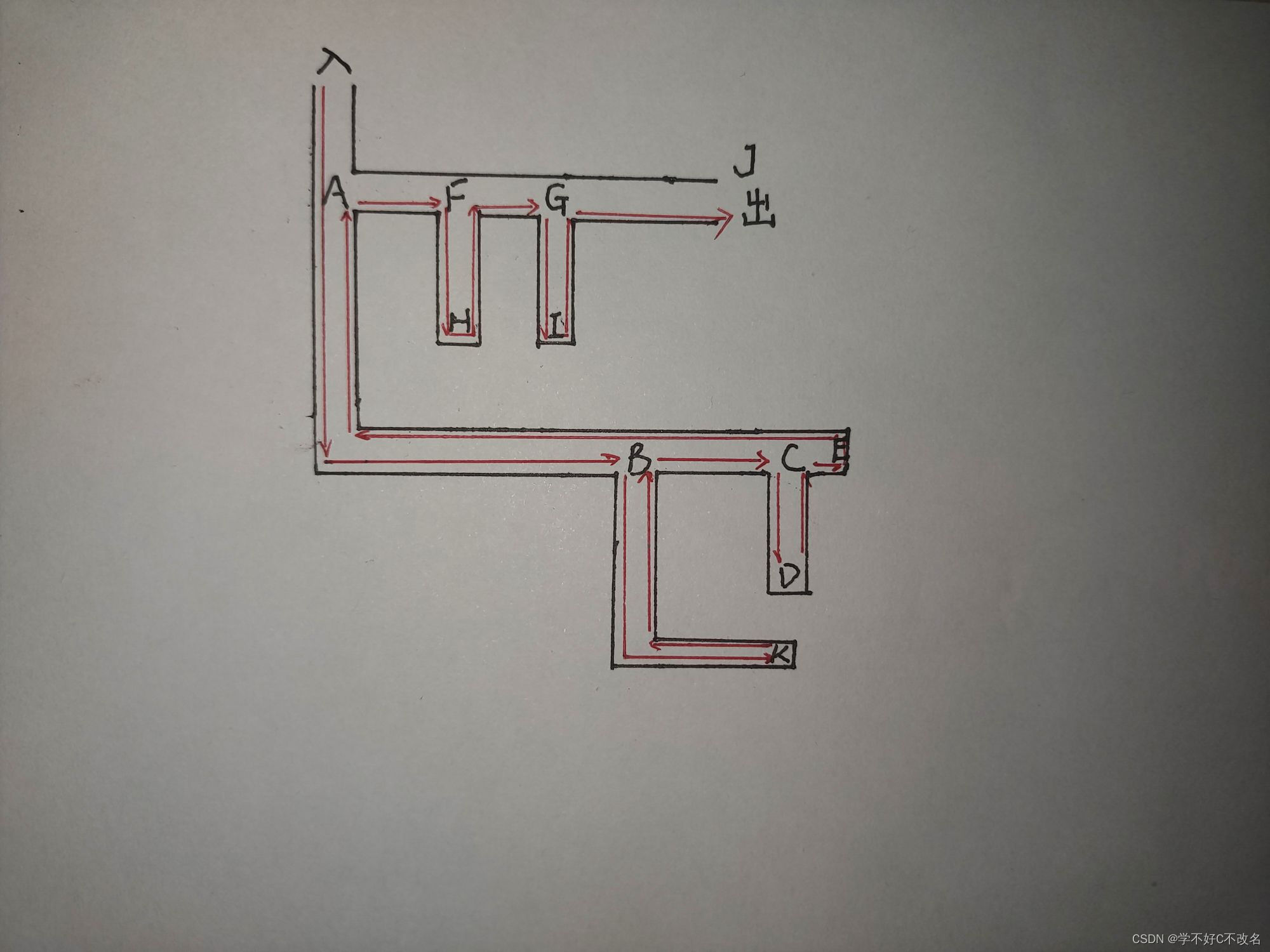
?如图所示,从入口进入后,当碰到岔路口时,我们可以靠着右墙走,如果碰到新的岔路口,继续沿着新的岔路口的右墙走,碰到死路就退回到最近的岔路口再选择另一条岔路口继续。这个过程中,始终是右边优先,且返回的条件取决于是否到达一条死路,这则是“深度”。这样的一种搜索方式被称为深度优先搜索(即DFS)。
那么如何来实现呢,从图中可以很明显的看出
1.第一条路先后访问的结点为ABK,在这时,K到了死路,所以退回到B。
2.接着,从B开始,依次经过CD,D到达死路,返回C,C->E仍然为死路,返回A.
3.同样的,从A开始,选择另一条岔路,到F分岔,到H为死路,再回到F,从F再到G,G分岔,到I又为死路,返回G,从G到J,走出迷宫。
可以看得出来,虽然荒诞,但是这种方法确实可行(突然就掌握了走迷宫的诀窍呢)。
我们再看看,满足就继续,不满足则返回,这与递归是不是有些相似,我们可以从递归的角度来理解DFS(其实栈也是,但是还不熟练,而且从递归的角度来讲更加容易理解)。大家还记得斐波那契数列吧,这是一道经典的递归的题,F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2).当F(n)分为F(n-1)和F(n-2)时,此时的F(n)就是一个岔路口,通过它可以到达F(n-1)和F(n-2)这两个结点,之后在进行F(n-1)和F(n-2)的计算时,又可以将F(n-1)和F(n-2)当成两个新的岔路口继续下去,当访问到F(0)和F(1)时,就为死路,这样来看,递归式为岔路口,递归边界为死路,DFS也好理解一些了。
????????但是正如之前所说,DFS有多种实现的方法,递归只是其中较为便捷的方法而已,总之,DFS还有许多值得去探索和深思的地方,我还得继续加油。