[数据结构与算法]在一个有序的数组中查找一个数字（二分查找法）

前言

---

博客主页：干脆面la的主页

? ? ? 对于同博主一样刚入门不久的，遇到二分查找法是否也总是一学就会，一写就废，今天就来为大家来详解一下二分查找，巩固知识的同时希望本文能对大家有帮助。

• 如果认为博主的文章对你有所帮助
• 欢迎三连加关注
• 你们的支持是我最大的动力！

---

话不多说，甘蔗！

目录

前言

1 为什么要用二分查找法？

2 什么是二分查找法？

3 图解二分查找法

?4 代码实现

1 为什么要用二分查找法？

? ? ? 假设在一个有10个数字的有序数组中查找一个数字n，大家首先想到的是不是用一个循环遍历这个数组，再用if语句判断数组中是否有一个数字与要查找的那个数字相同呢？如下图：

int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
	int n = 8;//要查找的数字是8
	int i = 0;
	for (i = 0; i < 10; i++)
	{
		if (arr[i] == n)
		{
			printf("找到了，下标是%d\n", i);
			break;
		}
	}
	if (i == 10)
		printf("没找到\n");
	return 0;
}

这样做固然没有问题，但是用这种方法查找，对于一个有10000个数字的数组，最坏的可能是这个数组中没有这个数字，那么便要循环10000次才结束循环，这么一来实现查找数字代码的复杂度就很大了，因此我们要用到二分查找法来解决问题。

2 什么是二分查找法？

引例：假设小A让你在1~100之内猜一个数字，最稳妥的方法就是找一个中间数字50，然后小A告诉你是高了还是低了，你猜测数字的范围便缩小了一半，然后再在那一半里面找中间的数字，以此类推......最多只要猜七次便能得到答案。

---

这样的算法让我们在一个相当大的基数里找一个数字会为我们节省大量时间——这便是二分查找法的意义

3 图解二分查找法

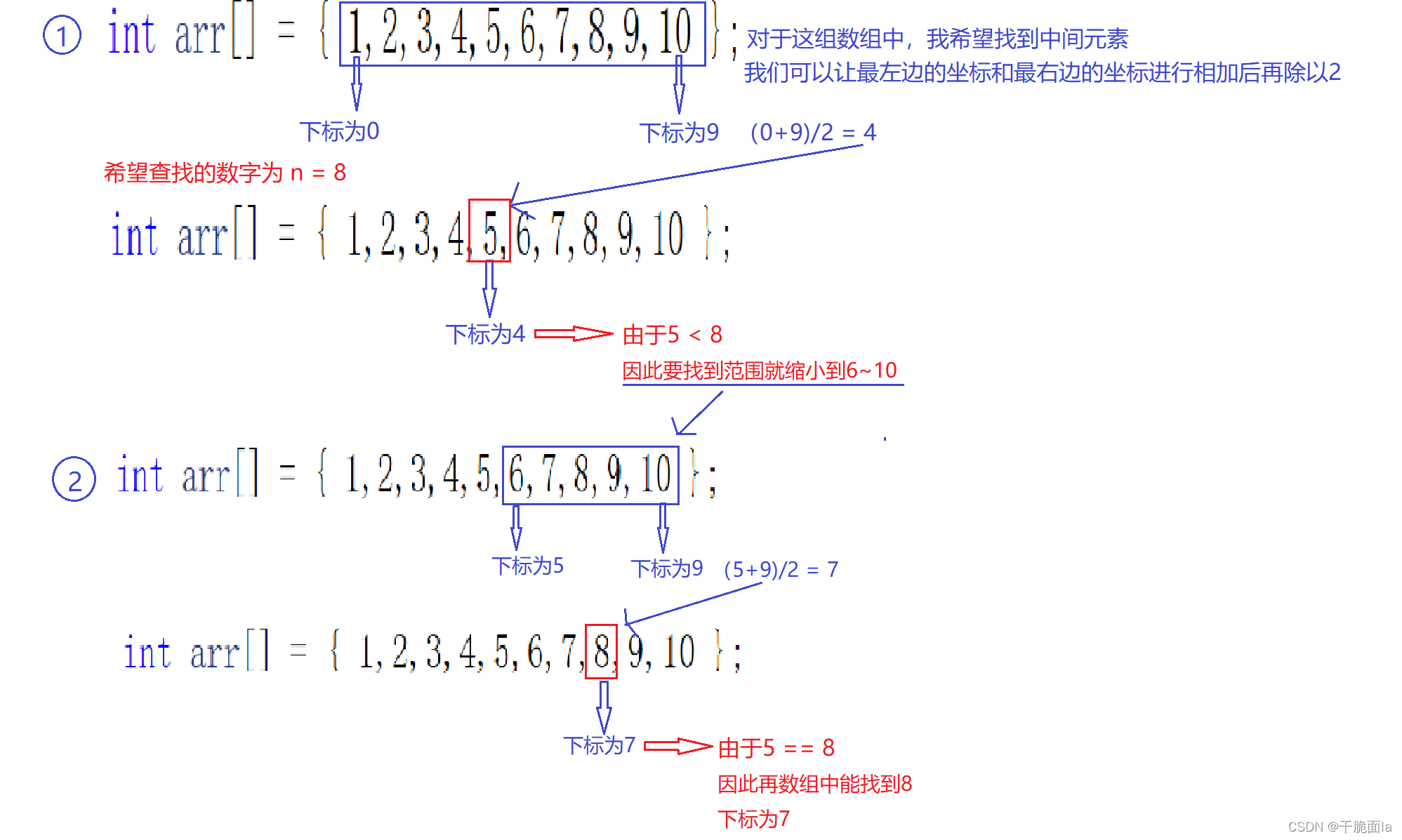
对于一个数组，我们可以找到其对应的左下标和右下标0和9，通过将其左右下标相加除以2来找到其中间元素4，再将其中间元素与要找的数字进行大小比较。

对于一个有序数组：

（1）如果中间元素<要找的数字，也就意味着这个数字不可能在中间元素的左边，左下标就由0变为5（其中间元素+1），此时对应的左下标和右下标为5和9，此时范围就缩小一半，以此类推......?

（2）如果中间元素>要找的数字，也就意味着这个数字不可能在中间元素的右边，右下标就由9变为3（其中间元素-1），此时对应的左下标和右下标为0和3，此时范围也缩小一半，以此类推......

---

?解析：由图解可知，每查找一次，我们要找的范围就缩小一半，因此二分查找法我们也称之为折半查找法。而对于本题想找到数字8更是通过两次二分查找就找到相应的结果，这就是二分查找法之所以经典的原因。

?4 代码实现

1. 确定数组元素个数 --> int sz = sizeof(arr) / sizeof(arr[0]) --> 40 / 4 = 10个元素
2. 确定左右下标 --> int left = 0; int right = sz - 1
3. 找中间元素 --> mid = (left + right) / 2
4. 通过中间元素与要找的数字大小比较来缩小范围

#include <stdio.h>
int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
	//1、计算元素个数
	int sz = sizeof(arr) / sizeof(arr[0]);
	int k = 8;//k为要再数组中找的数字
	//2、确定左右下标
	int left = 0;
	int right = sz - 1;
	while (left <= right)//只要left<=right说明left和right中间是有元素可以被查找的
	{
		//3、找中间元素
		int mid = (left + right) / 2;
		//4、通过比较大小缩小范围
		if (arr[mid] < k)
		{
			left = mid + 1;
		}
		else if (arr[mid] > k)
		{
			right = mid - 1;
		}
		else
		{
			printf("找到了，下标是%d\n", mid);
			break;
		}
	}
	if (left > right)
	{
		printf("找不到\n");
	}
	return 0;
}