数据结构入门——数组和字符串
文章目录
前言
??本系列文章将简要介绍数据结构课程入门知识,文章将结合我们学校(吉大)数据结构课程内容进行讲述。
一、数组
数组的存储和寻址
数组(Array)是有序的元素序列。若将有限个类型相同的变量的集合命名,那么这个名称为数组名。组成数组的各个变量称为数组的分量,也称为数组的元素,有时也称为下标变量。用于区分数组的各个元素的数字编号称为下标。数组是在程序设计中,为了处理方便, 把具有相同类型的若干元素按有序的形式组织起来的一种形式。这些有序排列的同类数据元素的集合称为数组。
对于高维数组的存储,可将其转化为一维来实现。因此必须对高维数组元素的存放次序进行约定。高维数组通常有两种存放次序约定——按行优先顺序和按列优先顺序,不同程序设计语言采用不同的存放顺序。如:在BASIC、Pascal和C/C++等程序设计语言中采用行优先顺序存放;在FORTRAN和MATLAB等语言中按列优先顺序存放。
行优先: 将高维数组元素按行向量顺序存储,第i+1个行向量存储在第i个后。
如行优先存储的二维数组A[m][n],设数组开始存放位置LOC(0,0),每个元素占用C个存储单元,则LOC(A[i][j])=LOC(0,0)+(i*m+i)*C.
设n维数组各维元素个数为 m1, m2, m3, …, mn 。
则下标为i1, i2, i3, …, in 的数组元素a[i1][i2]…[in]的存储地址
LOC(i1, i2, i3, …, in)=LOC (0,…,0 ) + ( i1 * m2 * m3 * … * mn + i2 * m3 * m4 * … * mn+ ……+ in-1 * mn + in) * C
列优先: 将数组元素按列向量的顺序存储,第i+1个列向量存储在第i个向量之后。
计算方法与行优先类似。
二.矩阵
矩阵的数组表示
一般采用二维数组存放矩阵。矩阵的运算一般有加减和矩阵相乘矩阵转置。
加减运算可以直接按照数组相加。
矩阵的乘法: 矩阵Am*p和Bp*n的乘积Cm*n其中第 i 行第 j 列元素cij为
∑
k
=
1
p
(
a
i
k
×
b
k
j
)
\sum_{k=1}^p (a_{ik}\times b_{kj} )
∑k=1p?(aik?×bkj?)
int** Multi(int** A, int** B, int m, int p, int n) {//A,B,m,p,n与上述含义一致
//新建矩阵C
int** C = new int* [m];
for (int i = 0; i < m; ++i) {
C[i] = new int[n] {0};
}
//乘法运算
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
C[i][j] = 0;
for (int k = 0; k < p; ++k)
C[i][j] = C[i][j] + A[i][k] * B[k][j];
}
return C;
}
矩阵转置:
int** Transpose(int** A, int m, int n) {//m行n列矩阵转置
int** B = new int* [n];
for (int i = 0; i < n; ++i)
B[i] = new int[m];
//转置
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
B[j][i] = A[i][j];
return B;
}
特殊矩阵的压缩存储
(1)对角矩阵的压缩存储
- 若n×n的方阵M是对角矩阵,则对所有的i≠j(1≤ i, j ≤ n) 都有M(i, j)=0,即非对角线上的元素均为0 . 非0元素只在对角线上
- 对于一个n×n的对角矩阵,至多只有n个非0元素,因此只需存储n个对角元素
- 可采用一维数组d[ ]来压缩存储对角矩阵
采用一维数组d[n]来压缩存储对角矩阵,其中d[i-1]存储M(i, i)的值。
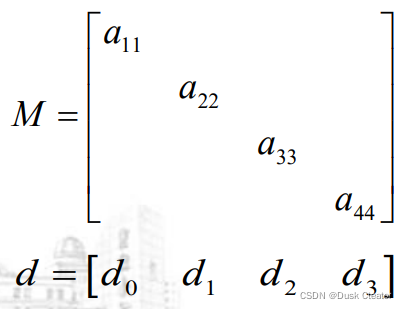
(2)三角矩阵的压缩存储
- 三角矩阵分为上三角矩阵和下三角矩阵
- 方阵M是上三角矩阵,当且仅当i>j时有M(i, j)=0

- 方阵M是下三角矩阵,当且仅当i<j时有M(i, j)=0
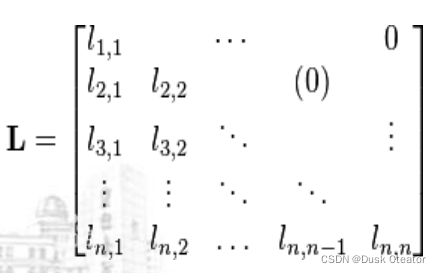
以下三角矩阵M为例,讨论其压缩存储方法:
将下三角矩阵压缩存放在一维数组d
- d需要多少个元素? n(n+1)/2
- M(i, j)在数组d的什么位置?
设元素M(i, j)前面有k个元素,可以计算出
k =1+2+…+ (i ?1) + (j?1)= i(i?1)/2 + (j?1)
M(i, j)映射到d中所对应的元素是d[k]
M(i, j) = d[k] = d[ i(i?1)/2 + (j?1) ]
(3)对称矩阵的压缩存储
因为对称矩阵中M(i, j)与M(j, i)的信息相同,所以只需存储M的下三角部分的元素信息。
将对称矩阵存储到一维数组d
- d需要多少个元素? n(n+1)/2
- M(i, j)的寻址方式是什么?
| 下三角元素 ( i ≥ j ) | 上三角元素 ( i < j ) |
|---|---|
| M(i, j)=d[k] k = i(i?1)/2 + (j?1) | M(i, j)=M(j, i)=d[q] q= j(j?1)/2 + (i?1) |
(4)三对角矩阵的压缩存储方法
方阵Mn×n中任意元素M(i, j),当 | i - j | >1时,有M(i, j) =0, 则M称为三对角矩阵。
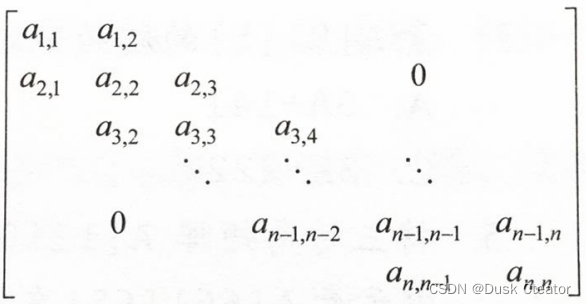
压缩方法:
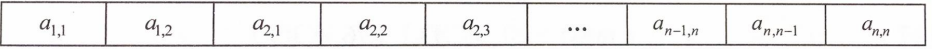
M(i, j)=d[k],k = 2+(i-2)*3+(j-i)+1=2i+j-3
三元组表与十字链表
稀疏矩阵的压缩存储
稀疏矩阵特点:零元素多,且其分布一般没有规律
压缩作用:仅存储非零元素,节省空间。
对于矩阵 Am*n 的每个元素aij,知道其行号i和列号j,就可以确定该元素在矩阵中的位置。因此,如果用一个结点来存储一个非零元素的话,那么该结点可以设计如下
| i | j | aij |
|---|
在三元组结点的基础上实现对整个稀疏矩阵的存储
顺序存储方式实现:三元组表
将表示稀疏矩阵的非零元素的三元组结点按行优先的顺序排列,得到一个线性表,将此线性表用顺序存储结构存储起来,称之为三元组表
例如:
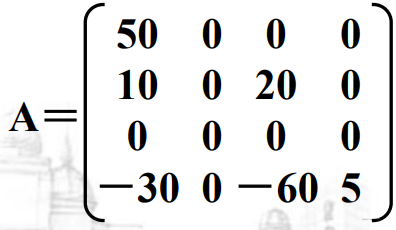
| B[0] | 1 | 1 | 50 |
|---|---|---|---|
| B[1] | 2 | 1 | 10 |
| B[2] | 2 | 3 | 20 |
| B[3] | 4 | 1 | -30 |
| B[4] | 4 | 3 | -60 |
| B[5] | 4 | 4 | 5 |
分析: 相应的算法描述较为简单,但对于非零元的位置或个数经常发生变化的矩阵运算就显得不太适合。
链接存储方式实现:十字链表
矩阵的元素结构:分别表示该元素的左邻非零元素、上邻非零元素、所在的行、所在的列和它的值。

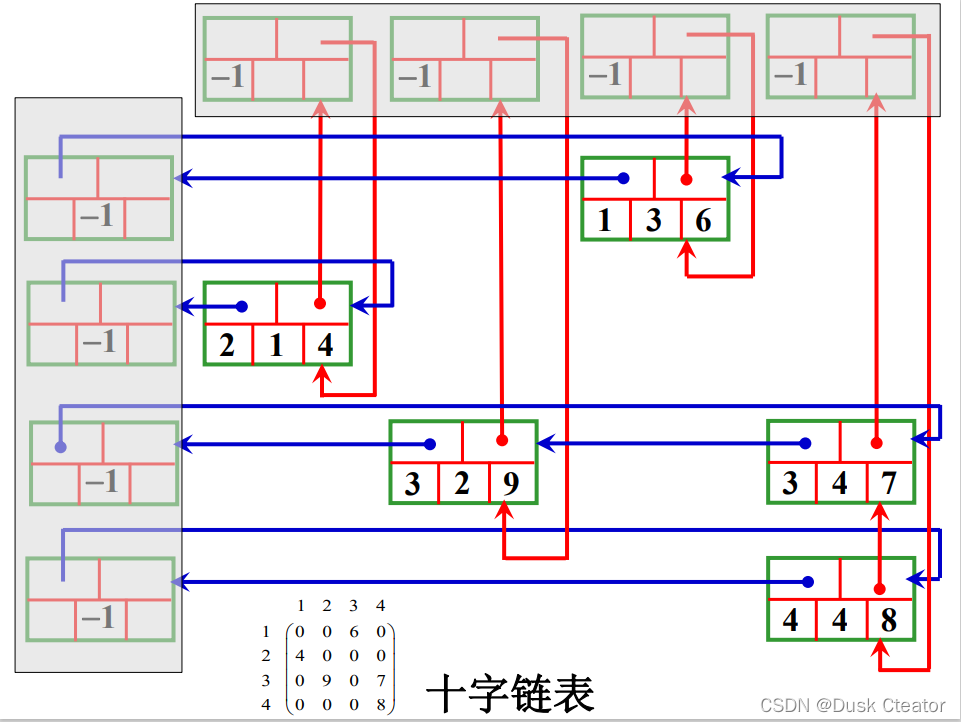
对矩阵的运算实质上就是在十字链表中插入结点、删除结点以及改变某个结点的数据域的值
三、字符串
字符串或串(String)是由数字、字母、下划线组成的一串字符。一般记为 s=“a1a2···an”(n>=0)。它是编程语言中表示文本的数据类型。在程序设计中,字符串(string)为符号或数值的一个连续序列,如符号串(一串字符)或二进制数字串(一串二进制数字)。
字符串模式匹配
模式匹配问题定义
在目标串中寻找模式串出现的首位置。
给定两个字符串S和P,目标串S有n个字符,模式串P有m个字符,m ≤ n。从S的第一个字符开始,搜索P,如果找到,返回P的第一个字符在S中的位置;如果没找到(即S中不包含P),则返回-1 。
模式匹配的应用:文本编辑器中常用的“查找”、“替换”
朴素模式匹配算法
朴素模式匹配算法(Brute Force算法,暴力算法)
算法思想:从目标串的的第一个字符起与模式串的第一个字符比较,若相等,则继续对字符进行后续的比较,否则目标串从第二个字符起与模式串的第一个字符重新比较,直至模式串中的每个字符依次和目标串中的一个连续的字符序列相等为止,此时称为匹配成功,否则匹配失败。
例:S= “abaaabab”, P = “abab”
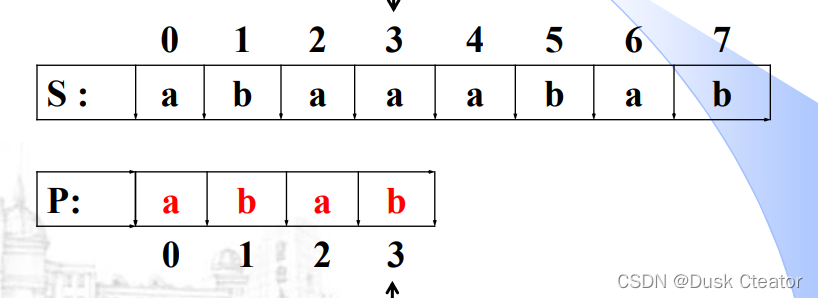
每次失配后:
模式串右移1位
指针i回退到i-j+1
指针j回退到0
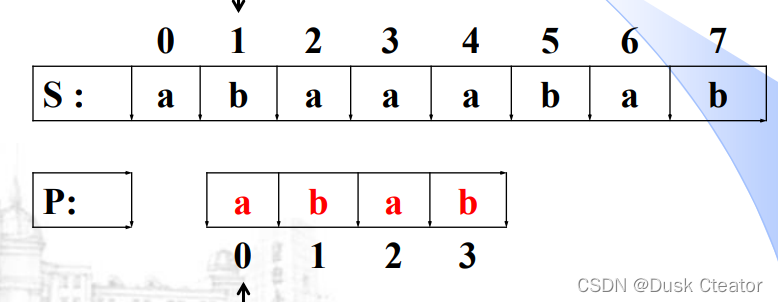
- 朴素模式匹配算法的优点是过程简单,缺点是效率比较低。朴素的模式匹配算法中存在回溯,这影响到匹配算法的效率,因而朴素的模式匹配算法在实际应用中很少采用。
- 关键运算:字符比较
- 时间复杂性为O(nm)
KMP算法
快速模式匹配KMP算法
| 朴素模式匹配存在的问题 (每次匹配失败后) | 可能的优化途径 |
|---|---|
| 模式串仅右移1位 | 模式串能否多移几位 |
| 目标串的匹配指针回退 | 指针可否不回退 |
| 模式串的匹配指针回退至0 | 指针可否不回退至0 |
一般情况:设目标S=s0, s1,……, sn?1, 模式串P=p0, p1,……, pm?1
假设当前正进行某 次 匹 配 , 有 stst+1……st+j= p0 p1……pj
但 st+j+1≠ pj+1,即在pj+1的位置失配
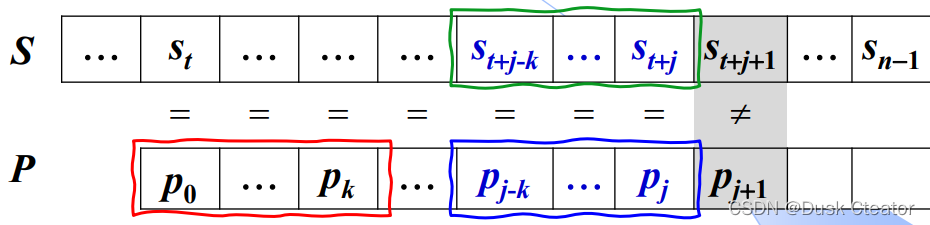
在失配位置前对应的子串p[0……j]中,找最长相等的前后缀,即使 p[0……k] = p[j-k …… j] 的最大k。
s[t+j?k……t+j] = p[j-k……j] = p[0……k]
k:p[0……j]的最长相等前后缀长度减1,其值只与模式串p的下标j有关,k =f ( j )
下次匹配时:
右移P使p[0……k] 与 s[t+j?k ……t+j ]对齐。
目标串匹配指针不动,模式串匹配指针只需回退到k+1,即模式串右移j-k 位
k 标识了p[0……j]的最长相等前后缀
k值组成的数组一般称为next数组,由失败函数生成

失败函数
void Fail(char P[], int f[], int m){
int k=f[0]=-1;
for(int j=1; j<m; j++){ //求f[j]
while(k>=0 && P[k+1]!=P[j])
k=f[k];//求p0…pk的最长相等前后缀
if(P[k+1]==P[j]) k++;
f[j]=k;
}
}
得到模式串的失败函数后KMP算法如下
int KMP(char S[], char P[], int n, int m){//目标串S长度为n,模式串P长度为m
int i=0, j=0; // i, j分别为S和P的匹配指针
int f[N]; //数组 f[ ]存放失败函数的值
Fail(P, f, m); //计算失败函数
while(j<m && i<n) {
if(S[i]==P[j]){ i++; j++;}
else if (j==0) i++; //若P第0个字符匹配失败,则从S的下个字符开始下次匹配
else j=f[j-1]+1; //确定P下次匹配位置
}
if (j==m) return i-m; //匹配成功
return -1; //匹配失败
}
KMP算法时间复杂度O(m+n)
失败函数其他用法
-
求字符串循环节
字符串长度为n
?循环节(最小重复单元)长度:L=n-f[n-1]-1
?字符串是否可由循环节完全循环组成:n%L=0 且 f[n-1]≠-1
?如果不能,需要补L-(n%L)个字符
-
最长重复子串
字符串长度为n
?第二长相等的前后缀长度f[f[n-1]]+1.
?最长重复前缀:失败函数数组中的最大值.
?最长重复子串:字符串p[i]…p[n-1]的失败函数是一个数组,该数组中的最大值标识以i开头的最长重复子串长度。现在要求是以任意字符开头的最长重复子串,所以可以外套一层i从0到n-1的循环即可。
BM算法
坏字符BM算法
每一趟比对,按照模式串下标从大到小(自右向左)的顺序进行比对
坏字符策略:
(1)没出现规则:P中不包含坏字符,则P整体移过失配位置。
(2)左端出现规则:P包含坏字符,且在失配位置的左端,让P中最右边的坏字符(失配位置左侧且与失配位置最近的坏字符)与失配位置对齐。
(3)右端出现规则:P包含坏字符,且在失配位置的右端,P右移1位。
-
若P中不含坏字符,则该坏字符与模式串P中的任何字符都不可能匹配,则P整体移过失配位置,即移动到坏字符后面的位置


-
若P中含有1个坏字符,找出P中的坏字符,让其与失配位置对齐。


-
若P中包含多个坏字符,让P中最右边的坏字符与失配位置对齐。


-
P中包含多个坏字符,最右边的坏字符过于靠右,在失配位置的右侧,此时将P右移1个字符


BC表:
每个字符在P中出现的最右位置预先存储在一个表BC中。
创建BC表
int* buildBC(char *P, int m){
int *BC=new int [256];
for(int i=0; i<256; i++) BC[i]=-1;
for(int i=0; i<m; i++) BC[ P[i] ]=i;
return BC;
}
BM算法
int BM(int*S,int*P,int n,int m){
int*BC=buildBC(P,m);
int i=0;
//看P是否在S的第i个位置
while(i<=n-m){
int j=m-1;//从右往左扫描,故j初始指向P最后一个字符
while(P[j]=S[i+j]){
if(j=0) return i;//P扫描完毕,匹配成功
j--;
}//S[i+j]为坏字符,bc[Si+j]为该字符在P中最右位置
if(j-BC[S[i+j]])
i+=j-BC[S[i+j]]//P右移
else i++;//P中坏字符在失配位置右侧,P右移1位
}
return -1;
}
- 若暂且不考虑预处理(构建BC表)的时间代价: 最好情况O(n/m)
- 单词匹配概率越小,性能优势越明显。
- P越长,效果越明显。
坏字符+好后缀BM算法
BM算法的好后缀策略
- 若P失配位置左方有与好后缀相等的子串,则选取最靠右的子串,让该子串与主串的好后缀对齐。
- 若P失配位置左方没有与好后缀相等的子串,则找P的最长前缀,该前缀与好后缀的某个后缀相等,然后该前缀与主串的好后缀对齐。
- 若P失配位置左方没有与好后缀相等的子串,且找不到与好后缀的某个后缀相等的前缀,意味着P一位一位右移的过程中都不可能有和S的好后缀匹配的子串,故将P整体右移至S的好后缀后面。
每次失配后,
P右移的位数 = max{ 坏字符策略算出的右移位数,好后缀策略算出的右移位 }
KMP算法与BM算法
- 当字符集规模较小时,单词比对的成功概率较高,KMP算法具有稳定的线性时间复杂度,更能体现出优势;采用BC策略的BM算法却不能大跨度向右移动。
- 当字符集规模较大时,单词比对的成功概率较小,KMP算法依旧保持线性时间复杂度;采用BC策略的BM算法会因比对失败的概率增加,大跨度地向右移动。