[数据结构与算法]链表基础知识与题目整理(Python)

1.链表简介

1.1 链表定义

链表(Linked List)： 一种线性表数据结构。它使用一组任意的存储单元（可以是连续的，也可以是不连续的），来存储一组具有相同类型的数据。
比如单链表：

如上图所示，链表通过将一组任意的存储单元串联在一起。

链表节点： 每个数据元素占用若干存储单元的组合称为一个链接点。

链表节点的存储内容: 数据元素的值+后继指针（后继指针是指出这个数据元素在逻辑关系上的直接后继元素所在链节点的地址）。

数据之间的逻辑关系：逻辑关系是通过后继指针来简介反映的。逻辑上相邻的数据数素在物理地址上可能相邻，也可能不相邻。其在物理地址上的表现是随机的。

链表的优缺点：
优点：存储空间不必事先分配，在需要存储空间的时候可以临时申请，不会造成空间的浪费；一些操作的时间效率远比数组高（插入、移动、删除元素等）。
缺点：不仅数据元素本身的数据信息需要占用存储空间，后继指针也需要占用存储空间，链表结构比数组结构的空间开销大。

1.2 双向链表

双线链表（Doubly Linked List：链表的一种，也叫做双链表。它的每个链节点中有两个指针，分别指向后继和前驱。

1.3 循环链表

循环链表（Circular Linked List)：链表的一种。它的最后一个链节点指向头节点，形成一个环。

2.链表的基本操作

以单链表为例介绍数据结构的增、删、改、查4种情况。

2.1 链表的结构定义

链表是由链节点通过next链接而构成的，所以需要先定义一个简单的链节点类，即ListNode类：
ListNode类使用成员：val表示数据元素的值，使用指针标量next表示后继指针。
在创建空链表时，只需要把相应的链表头节点变量设置成空链接即可。在Python里可以将其设置为None，其它语言也有类似值。

# 链节点类
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val       # 数据域
        self.next = next     # 指针域

# 链表类
class LinkedList:
    def __init__(self):
        self.head = None  # 初始化头节点

2.2 建立一个线性链表

建立一个线性链表的过程是：根据线性表的数据元素动态生成链节点，并依次将其连接到链表种。具体做法如下：

• 从第1个数据元素开始依次获取表中的数据元素。
• 每取一个数据元素，就为该数据生成一个新节点，将新节点插入到链表的尾部。
• 插入完毕之后返回第1个链节点的地址

建立一个线性链表的时间复杂度为 O（n)，n 为线性表长度。

建立一个线性链表的代码如下：

# 根据 data 初始化一个新链表
def create(self, data):
    self.head = ListNode(0)
    cur = self.head        
    for i in range(len(data)):
        node = ListNode(data[i])
        cur.next = node
        cur = cur.next

2.3 求线性链表的长度

线性链表的长度被定义为链表中包含的链节点的个数。求线性链表的长度操作只需要使用一个可以顺着链表指针移动的指针变量 cur 和一个计数器 count。具体做法如下：

• 让指针变量 cur 指向链表的第 1 个链节点。
• 然后顺着链节点的 next 指针遍历链表，指针变量 cur 每指向一个链节点，计数器就做一次计数。
• 等 cur 指向为空时结束遍历，此时计数器的数值就是链表的长度，将其返回即可。

求线性链表长度的时间复杂度为 O（n)，n 为线性表长度。

求线性链表长度

# 获取链表长度
def length(self):
    count = 0
    cur = self.head
    while cur:
        count += 1
        cur = cur.next 
    return count

2.4查找链表中的元素

在链表中查找值为 val 的位置：链表不能像数组那样进行随机访问，只能从头节点 head 开始，沿着链表一个一个节点逐一进行查找。如果查找成功，返回被查找节点的地址。否则返回 None。

查找链表中的元素的时间复杂度为 O（n)，n 为线性表长度。

查找链表中元素的代码如下

# 查找元素
def find(self, val):
    cur = self.head
    while cur:
        if val == cur.val:
            return cur
        cur = cur.next
    return None

2.5插入元素

链表中插入元素操作分为三种：
第一种：链表头插入元素：在链表第1个链接点之前插入val的链接点。
第二种：链表尾部插入元素：在链表最后1个链节点之后插入值为val的链节点。
第三种：链表中间插入元素：在链表第i个链节点之间插入值为val的链接点。

2.5.1 链表头插入元素

算法实现的步骤为：
第一步：先创建一个值为val的链节点node。
第二步：将node的next指针指向链表的头节点head。
第三步：再将链表的头head指向node
如下图所示：

因为表头插入链节点与链表的长度无关系，所以该算法的时间复杂度为O(1)。
代码如下：

# 头部插入元素
def insertFront(self, val):
    node = ListNode(val)   # 创建node
    node.next = self.head  # 将原先头地址赋给新node的next
    self.head = node       # 将node的地址作为整个链表头

2.5.2 尾部插入元素

实现步骤：
第一步：创建一个值为val的链节点node
第二步：使用指针cur指向链表的头节点head
第三步：通过链节点的next指针移动cur指针，从而遍历链表，直到cur.next == None。
第四步：令cur.next指向将新的链节点node

因为将 cur 从链表头部移动到尾部的操作次数是 n 次，所以该算法的时间复杂度是 O(n）。

# 尾部插入元素
def insertRear(self, val):
    node = ListNode(val)
    cur = self.head
    while cur.next:    # 将cur移到最后值的位置
        cur = cur.next
    cur.next = node    # 将新的位置地址赋给旧链表最后一个数的next

2.5.3 中间插入元素

实现步骤如下：
第一步：使用指针变量cur和一个计数器count。令cur指向链表的头节点，count初始值赋值为0。
第二步：沿着链节点的next指针遍历链表，指针变量cur每指向一个链节点，计数器就做一次计数。
第三步：当count==index-1时，说明遍历道了第index-1个链节点，此时停止遍历。
第四步：创建一个为val的链节点node。
第五步：将node.next指向cur.next。
第六步：令cur.next指向node。
详细内容如下图所示：


代码如下:

# 中间插入元素
def insertInside(self, index, val):
    count = 0
    cur = self.head
    # 先找到要插入的位置
    while cur and count < index - 1: 
        count += 1
        cur = cur.next
    # 如果不存在，报错  
    if not cur:
        return 'Error'
    # 创建node
    node = ListNode(val)
    # node.next 指向cur.next
    node.next = cur.next   # cur.next原先存储的是下一个值的地址
    
    cur.next = node       # 现在需要跟新cur.next跟新成新建node的地址

2.6 改变元素

目标：将链表中第i个元素值改为val
步骤：
第一步：使用指针变量cur和一个计数器count。令cur指向链表的头节点，count初始值赋值为0。
第二步：沿着链节点的next指向遍历链表，指针变量cur每指向一个链节点，计数器就做一次。
第三步：当count==index时，说明遍历得到了第index个链节点，此时停止遍历。
第四步：直接更改cur值val
时间复杂度：O(n)
代码如下

# 改变元素
def change(self, index, val):
    count = 0
    cur = self.head
    # 寻找要修改的位置
    while cur and count < index:
        count += 1
        cur = cur.next
    # 如果不存在则报错   
    if not cur:
        return 'Error'
    # 跟新值
    cur.val = val

2.7 删除元素

目标：链表中第i个元素
三种情况：
第一种：链表头部删除元素：删除链表的第1个链节点
第二种：链表尾部删除元素：删除链表末尾最后1个链节点
第三种：链表中间删除元素：删除链表第i个链节点

2.7.1 链表头部删除元素

一步搞定：直接将self.head沿着next指向右移动一步即可。

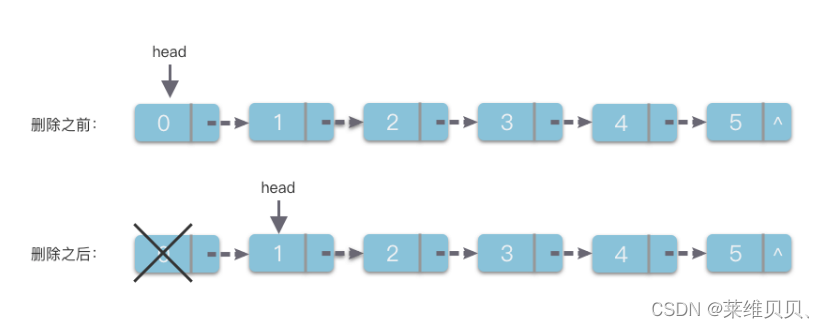
时间复杂度：O(1)
代码如下

# 链表头部删除元素
def removeFront(self):
    if self.head:
        self.head = self.head.next

2.7.2链表尾部删除元素

步骤：
第一步：使用指针变量cur沿着next指针移动到倒数第2个链节点。
第二步：将此节点的next指针指向None即可。

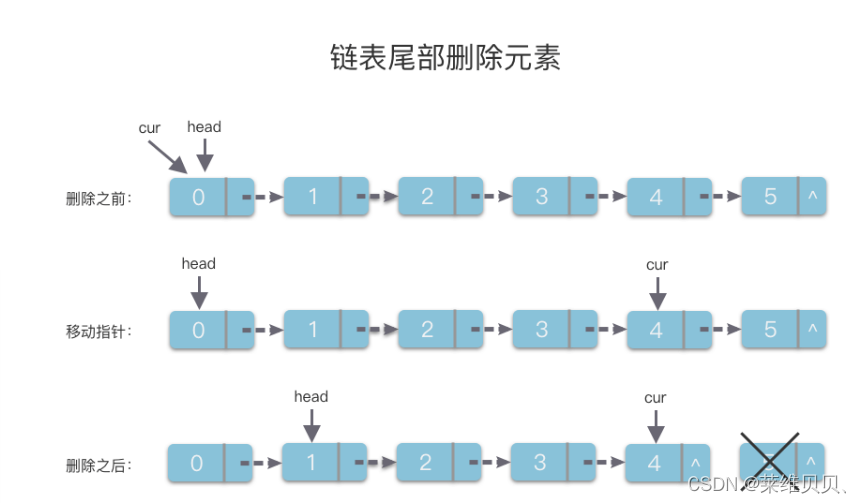
时间复杂度：O(n)
代码如下

# 链表尾部删除元素
def removeRear(self):
    if not self.head.next:
        return 'Error'

    cur = self.head
    while cur.next.next: # 判断条件是指所指向的地址为空结束
        cur = cur.next
    cur.next = None

2.7.3链表中间删除元素

目标：删除第i个元素
步骤：
第一步：先使用指针变量cur移动到第i-1个位置的链节点
第二步：然后将cur的next指针，指向要第i个元素的下一个节点即可

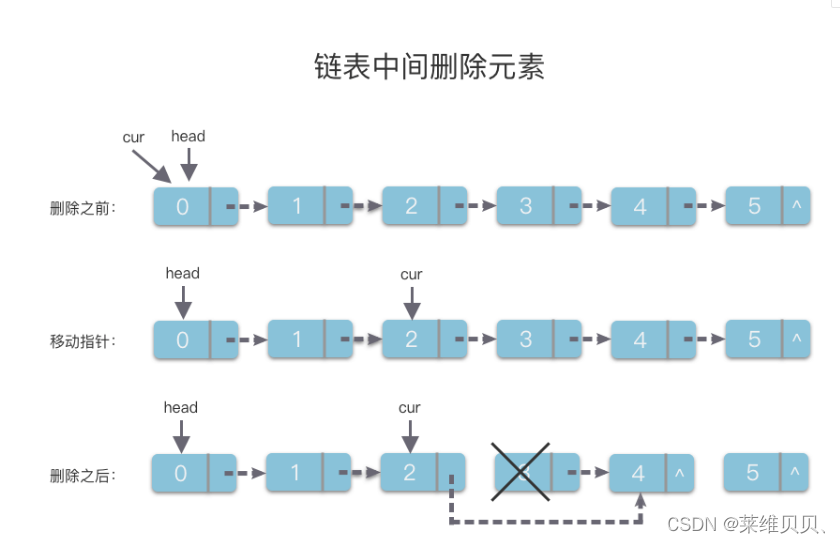
时间复杂度：O(n)
代码如下

# 链表中间删除元素
def removeInside(self, index):
    count = 0
    cur = self.head
    # 寻找位置
    while cur.next and count < index - 1:
        count += 1
        cur = cur.next
        
    if not cur:
        return 'Error'
    # 更换cur.next的所指向的地址    
    del_node = cur.next
    cur.next = del_node.next

3. 知识点总结

1. 链表是实现线性表的链式存储结构的基础
2. 链表最大优势在于灵活的添加和删除元素
3. 链表访问元素、改变元素的时间复杂度为O(n)
4. 链表头部插入、删除元素的时间复杂度为O(1)
5. 链表尾部插入、删除操作的时间复杂度为O(n)
6. 而普通情况下的删除元素操作的时间复杂度都为O(n)，比如数组

3.链表相关题目

题一：设计链表

链接：https://leetcode-cn.com/problems/design-linked-list/

class Node(object):
    def __init__(self, x):
        self.val = x
        self.next = None # 初始化头节点

class MyLinkedList:

    def __init__(self):
        self.head = Node(0)

    def get(self, index: int) -> int:
        if index < 0 : return -1
        cur = self.head
        count  = 0
        # 第一种： cur.next == None， count != index，返回-1
        # 第二种： cur.next == None， count == index， 返回cur.val
        # 第三种： cur.next != None， count == index ，返回cur.val
        while cur.next and count < index:
            count  += 1
            cur = cur.next
        if count != index:
            return -1
        else:
            return cur.val

    def addAtHead(self, val: int) -> None:
        # 将节点添加到头
        new_node = Node(val)
        new_node.next = self.head.next
        self.head = new_node

    def addAtTail(self, val: int) -> None:
        # 将节点添加到尾
        new_node = Node(val)
        cur = self.head
        while cur.next:
            cur = cur.next
        cur.next = new_node

    def addAtIndex(self, index: int, val: int) -> None:
        # 将节点插到index前面
        new_node = Node(val)
        cur = self.head
        count = 0
        # 当idnex小于0时候，添加到头
        if index < 0:
            new_node.next = self.head.next
            self.head = new_head
        # 第一种： cur.next == None， count < index，不添加
        # 第二种： cur.next == None， count = index，添加
        # 第三种： cur.next != None， count == index ，添加
        while cur.next and count < index:
            count +=1
            cur = cur.next
        # 当index大于链表长度，不添加
        if count == index:
             # 尾部添加
             if cur.next is None:
                 cur.next = new_node
             else:
            # 链表间添加
                 new_node.next = cur.next
                 cur.next = new_node 

    def deleteAtIndex(self, index: int) -> None:
        # index小于0不删除
        if index < 0:
            return
        cur = self.head
        count = 0
        # 第一种：当cur.next.next == None，当count < index ，不删除
        # 第二种：当cur.next.next != None，count==index     ，删除链表间
        # 第三种：当cur.next.next == None，count==index     ，删除尾部
        while cur.next.next and count < index:
            count +=1
            cur = cur.next
        if count == index:
            if cur.next.next is None:
                cur.next = None
            else:
                # 更换cur.next所指向的地址
                del_node = cur.next
                cur.next = del_node.next

题二：反转列表

题链接：https://leetcode-cn.com/problems/reverse-linked-list/
图解：

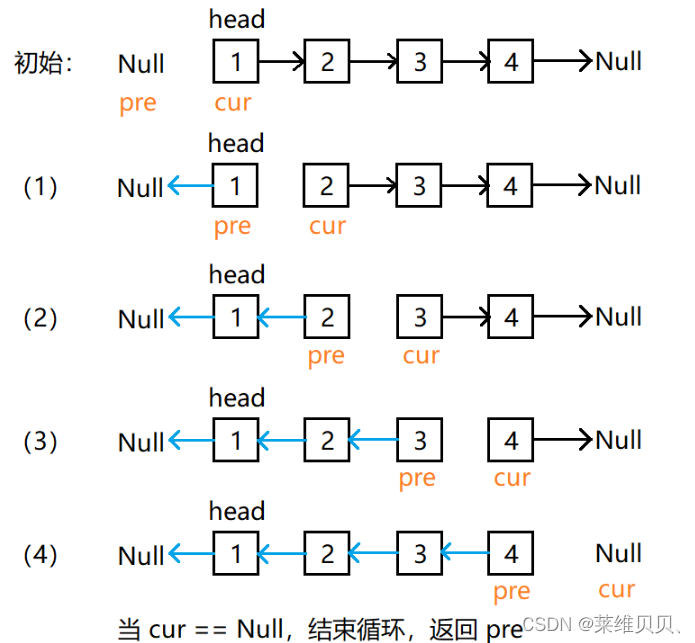
class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        pre = None
        cur = head
        while cur:
            temp = cur.next   # 先把原来cur.next位置存起来
            cur.next = pre
            pre = cur
            cur = temp
        return pre

题三：移除原表元素

题链接：https://leetcode-cn.com/problems/remove-linked-list-elements/
代码

class Solution:
    def removeElements(self, head: ListNode, val: int) -> ListNode:
        # 第一步：建立额外头，使遍历从原头开始
        dummy = ListNode()
        dummy.next = head   # 将额外头与原头相连
        cur = dummy
        # 第二步： 开始从原头开始遍历
        while cur:
            if cur.next and cur.next.val == val:
                # 跳过cur.next所指向的节点，直接链接val值的下一个节点
                cur.next = cur.next.next
            else:
                cur = cur.next
        return dummy.next

题四：奇偶链表

图解：


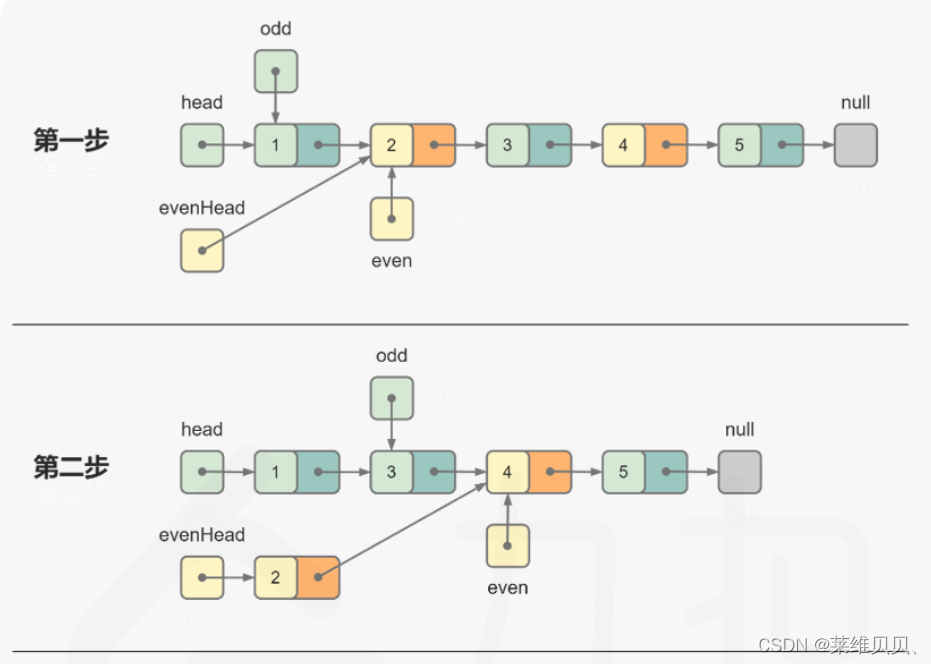
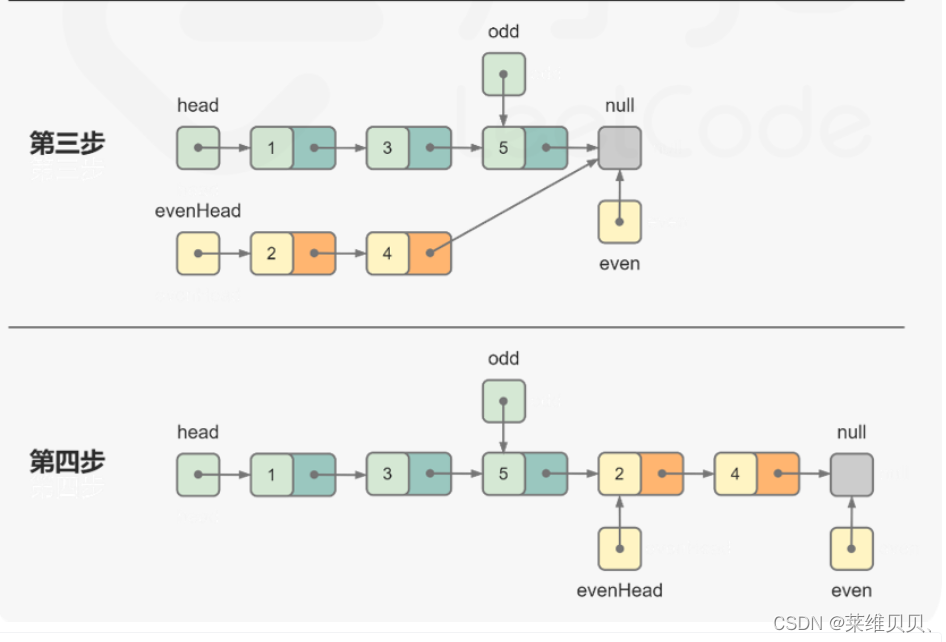
代码

class Solution:
    def oddEvenList(self, head: ListNode) -> ListNode:
        if not head:
            return head
        # 偶数头保存
        evenHead = head.next
        # odd为奇，even为偶数
        odd,even = head,evenHead
        #
        while even and even.next:
            # 奇数节点直接链偶数节点的下一个节点,该节点即为偶节点
            odd.next = even.next
            # 移动节点
            odd = odd.next
            # 偶数节点直接链奇数节点的下一个节点,该节点即为奇节点
            even.next = odd.next
            # 更新节点
            even = even.next
        # 链接奇偶节点
        odd.next = evenHead
        return head

题五：回文链表

题目链接：https://leetcode-cn.com/problems/palindrome-linked-list/
代码一：暴力

class Solution:
    def isPalindrome(self, head: ListNode) -> bool:
        # 思路：将链表中的数拿到列表中，再判断是否为回文
        if head.next is None:
            return True
        lis = []
        cur = head
        # 结束条件，当cur为空值时候结束
        while cur:
            lis.append(cur.val)
            cur = cur.next
        # 遍历判读从左向右是否与从右向左相等
        for i in range(len(lis)):
            if lis[i] != lis[-i-1]:
                return False
        return True

代码二

class Solution:
    def isPalindrome(self, head: ListNode) -> bool:
        # 空值或者一个值时为回文
        if not head or not head.next:
            return True
        #  定义链表反转函数
        def reversenode(head):
            # 用于暂存内容
            pre = None
            while head:
                # 暂存下个个节点
                temp = head.next
                # 转换指针
                head.next = pre
                # 暂存head目前节点 pre
                pre = head
                # 跟新head
                head = temp
            return pre
        # 将指针移到最后
        slow,fast = head,head # 快慢指针
        while(fast and fast.next):
            slow = slow.next
            fast = fast.next.next
        # 进行链表反转
        slow = reversenode(slow) 
        # 进行比对
        while(head and slow):
            if head.val != slow.val:
                return False
            head = head.next
            slow = slow.next
        return True

4.链表排序

4.1 链表排序简介

链表排序，因为链表不支持随机访问，访问链表后的节点只能依靠next指针从头部顺序遍历，所以相对于数组排序问题来说，链表排序问题会更加复杂一点。
总结一下适合链表排序与不适合链表排序的算法：

• 适合链表的排序算法：冒泡排序、选择排序、插入排序、归并排序、快速排序、计数排序、桶排序、基数排序。
• 不适合链表的排序算法：希尔排序。
• 可以用于链表排序但不建议使用的排序算法：堆排序。

希尔排序为什么不适合链表排序？
答： 希尔排序中经常涉及到对序列中第 i + gap 的元素进行操作，其中 gap 是希尔排序中当前的步长。而链表不支持随机访问的特性，导致这种操作不适合链表，因而希尔排序算法不适合进行链表排序。
为什么不建议使用堆排序？
答： 堆排序所使用的最大堆 / 最小堆结构本质上是一棵完全二叉树。而完全二叉树适合采用顺序存储结构（数组）。因为数组存储的完全二叉树可以很方便的通过下标序号来确定父亲节点和孩子节点，并且可以极大限度的节省存储空间。

重点是掌握 「链表插入排序」、「链表归并排序」 这两种排序算法。

4.2 链表插入排序

4.2.1 链表插入排序算法思路

1. 先使用哑节点dummy_head构造一个指向head的指针，使得可以从head开始遍历。
2. 维护sorted_list为链表的已排序部分的最后一个节点，初始时，sorted_list=head
3. 维护prev为插入元素位置的前一个节点，维护cur为待插入元素。初始时，prev=head，cur=head.next
4. 比较sorted_list 和 cur 的节点值。

• 如果 sorted_list.val <= cur.val，说明 cur 应该插入到 sorted_list 之后，则将sorted_list 后移一位。
• 如果 sorted_list.val > cur.val，说明 cur 应该插入到 head 与 sorted_list 之间。则使用prev 从 head 开始遍历，直到找到插入 cur 的位置的前一个节点位置。然后将 cur 插入。

5. 令cur = sorted_list.next，此时cur为下一个待插入元素
6. 重复4、5步骤，之后cur遍历结束为空。返回dummy_head的下一个节点。

def insertionSort(self, head: ListNode):
    if not head and not head.next:
        return head
    # 创建哑节点，使得遍历从head开始
    dummy_head = ListNode(-1)
    # 将哑节的下一个节点指向head
    dummy_head.next = head
    # sorted_list为链表的已排序部分的最后一个节点，初始时，sorted=head
    sorted_list = head
    # 为待插入元素
    cur = head.next 
    # 开始遍历
    while cur:
        # 如果待插入元素大于sorted_val中元素，直接插在后面
        if sorted_list.val <= cur.val:
            # 将 cur 插入到 sorted_list 之后
            sorted_list = sorted_list.next 
        # 将待插入元素插入前面
        else:
            prev = dummy_head
            # 从头开始遍历找到值比待插值大的，插入其前面
            while prev.next.val <= cur.val:
                prev = prev.next
            # 将 cur 到链表中间
            # cur插入中间之后，需要跳过原先cur连接cur.next
            sorted_list.next = cur.next
            # 此时prev.val大于cur：   pre -> cur ->  pre的下一个值
            cur.next = prev.next 
            prev.next = cur
        cur = sorted_list.next 
    
    return dummy_head.next

4.3 链表归并排序

4.3.1 链表归并排序算法思路

• 分割环节：找到链表中心链节点，从中心节点将链表断开，并递归进行分割。
  1. 使用快慢指针 fast = head.next、slow = head，让 fast 每次移动 2 步，slow 移动 1 步，移动到链表末尾，从而找到链表中心链节点，即 slow。
  2. 从中心位置将链表从中心位置分为左右两个链表 left_head 和 right_head，并从中心位置将其断开，即 slow.next = None。
  3. 对左右两个链表分别进行递归分割，直到每个链表中只包含一个链节点

• 归并环节：将递归后的链表进行两两归并，完成一遍后每个子链表长度加倍。重复进行归并操作，直到得到完整的链表。

1. 使用哑节点 dummy_head 构造一个头节点，并使用 cur 指向 dummy_head 用于遍历。
   比较两个链表头节点 left 和 right 的值大小。将较小的头节点加入到合并后的链表中。并向后移动该链表的头节点指针。
2. 然后重复上一步操作，直到两个链表中出现链表为空的情况。
3. 将剩余链表插入到合并中的链表中。
   将哑节点 dummy_dead 的下一个链节点 dummy_head.next 作为合并后的头节点返回。

def merge(self, left, right):
    # 归并环节
    dummy_head = ListNode(-1)
    cur = dummy_head
    while left and right:
        if left.val <= right.val:
            cur.next = left
            left = left.next
        else:
            cur.next = right
            right = right.next
        cur = cur.next
    
    if left:
        cur.next = left
    elif right:
        cur.next = right
        
    return dummy_head.next
    
def mergeSort(self, head: ListNode):
    # 分割环节
    if not head or not head.next:
        return head
    
    # 快慢指针找到中心链节点
    slow, fast = head, head.next
    while fast and fast.next:
        slow = slow.next 
        fast = fast.next.next 
    
    # 断开左右链节点
    left_head, right_head = head, slow.next 
    slow.next = None
    
    # 归并操作
    return self.merge(self.mergeSort(left_head), self.mergeSort(right_head))

5.链表双指针知识

5.1 双指针简介

双指针（Two Pointers）：指的是在遍历元素的过程中，不是使用单个指针进行访问，而是使用两个指针进行访问，从而达到相应的目的。如果两个指针方向相反，则称为「对撞时针」。如果两个指针方向相同，则称为「快慢指针」。如果两个指针分别属于不同的数组 / 链表，则称为「分离双指针」。

5.1.1 起点不一致的快慢指针

**起点不一致的快慢指针：**指的是两个指针从同一侧开始遍历链表，但是两个指针的起点不一样。 快指针 fast 比慢指针 slow 先走 n 步，直到快指针移动到链表尾端时为止。
试用范围：主要用于找到链表中倒数第 k 个节点、删除链表倒数第 N 个节点等。
列题：19. 删除链表的倒数第 N 个结点
思路：
使用起点不一致的快慢指针。让快指针 fast 先走 n 步，然后快指针、慢指针再同时走，每次一步，这样等快指针遍历到链表尾部的时候，慢指针就刚好遍历到了倒数第 n 个节点位置。将该位置上的节点删除即可。
注意：需要删除的节点可能包含了头节点。我们可以考虑在遍历之前，新建一个头节点，让其指向原来的头节点。这样，最终如果删除的是头节点，则删除原头节点即可。返回结果的时候，可以直接返回新建头节点的下一位节点。

代码：

class Solution:
    def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
        # 添加0头
        newHead = ListNode(0, head)
        # 快指针
        fast = head
        # 慢指针
        slow = newHead
        # 假设总步伐X，fast先走n步，还剩X-n步
        while n:
            fast = fast.next
            n -= 1
        # fast与slow同时走X-n步，fast到达终点，slow到达n点处
        while fast:
            fast = fast.next
            slow = slow.next
        # 跳过倒数第n节点
        slow.next = slow.next.next
        return newHead.next

5.1.2 步长不一致的快慢指针

步长不一致的慢指针：指的是两个指针从同一侧开始遍历链表，两个指针的起点一样，但是步长不一致。例如，慢指针 slow 每次走 1 步，快指针 fast 每次走两步。直到快指针移动到链表尾端时为止。
适用范围 步长不一致的快慢指针适合寻找链表的中点、判断和检测链表是否有环、找到两个链表的交点等问题。
例题：
141. 环形链表

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
    
        # 空链表或链表只有一个节点，无环
        if not head or head.next == None:
            return False
        # 初始化快慢指针
        fast = slow = head
        # 如果不存在环，肯定 fast 先指向 null
        # 细节：fast 每次走 2 步，所以要确定 fast 和 fast.next 不为空，不然会报执行出错。
        # 如果存在环，fast进入环里打转圈，slow一步一步的进入圈，fast与slow总会相遇
        while fast and fast.next:
            # 快指针移动 2 步，慢指针移动 1 步
            fast = fast.next.next
            slow = slow.next
            # 快慢指针相遇，有环
            if fast == slow:
                return True
        return False

5.1.3 分离双指针

分离双指针：两个指针分别属于不同的链表，两个指针分别在两个链表中移动。
适用范围：分离双指针一般用于有序链表合并等问题。
求解步骤：

• 使用两个指针 left_1、left_2。left_1 指向第一个链表头节点，即：left_1 = list1，left_2指向第二个链表头节点，即：left_2 = list2。
• 当满足一定条件时，两个指针同时右移，即 left_1 =left_1.next、left_2 = left_2.next。 当满足另外一定条件时，将 left_1 指针右移，即 left_1 =left_1.next。
• 当满足其他一定条件时，将 left_2 指针右移，即 left_2 = left_2.next。
• 当其中一个链表遍历完时或者满足其他特殊条件时跳出循环体。
  伪代码

left_1 = list1
left_2 = list2

while left_1 and left_2:
    if 一定条件 1:
        left_1 = left_1.next
        left_2 = left_2.next
    elif 一定条件 2:
        left_1 = left_1.next
    elif 一定条件 3:
        left_2 = left_2.next

例题
21. 合并两个有序链表

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        # 添加哨兵节点 prehead，方便链表的维护和返回
        prehead = ListNode(-1)
        # 添加维护节点pre，维护下一个next
        pre = prehead
        while list1 and list2:
            if list1.val<=list2.val:
                pre.next = list1
                list1 = list1.next
            else:
                pre.next = list2
                list2 = list2.next
            # 将pre指向下一个节点
            pre = pre.next
        # list1和list2有可能没合并完的，直接添加到pre后面
        pre.next = list1 if list1 is not None  else list2

        return prehead.next

参考链接

[1] https://algo.itcharge.cn
[2] 数据结构教程 第 2 版 - 唐发根 著
[3] 数据结构与算法 Python 语言描述 - 裘宗燕 著