//1.快排 强调两点 (1)分治(首先在该段数组区间中选取一个中间值作比较,此中间值可以任选比如两端或中间,但是选择中间这样效率高) (2)递归 递归时需要注意边界
对x位置小结:
如果区间取[l,i-1]和[i,r]这种,那么x不应该取左边界(l、(l+r)/2)。
应取 x = q[r]; x = q[(l+r+1)/2];
如果区间取[l,j]和[j+1,r]这种,那么x不应该取右边界(如r、(l+r+1)/2)。
应取 x = q[l]; x = q[(l+r)/2]; 可以自己取【0,1】感受一下
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args)throws IOException{
BufferedReader reader= new BufferedReader(new InputStreamReader(System.in));
int n=Integer.parseInt(reader.readLine());
String[] str=reader.readLine().split(" ");
int[] str1=new int[n];
for(int i=0;i<n;i++){
str1[i]=Integer.parseInt(str[i]);
}
quick_sort(str1,0,n-1);
for(int i=0;i<n;i++){
System.out.print(str1[i]);
}
reader.close();
}
static void quick_sort(int[] num,int l,int r){
if(l>=r){return;}
int q=num[(l+r)/2];int i=l-1;int j=r+1;
while(i<j){//i<j 考虑为i>j||i=j两种情况均退出
do i++ ;while(num[i]<q);//如果用while即每次先判断再加一的话,比如当num[i]=num[j]=num[x]的时候,即便交换后还是跟没交换一样所以while不断循环,
//用dowhile要保证他每一次交换完都先往前走再判断
//这里不加等号也是有讲究的,我认为是防止越界,例如边界等于q的时候
do j-- ;while(num[j]>q);
if(i<j){ //i<j的限制要加,谁知道while完后是不是有i<j了
int temp=num[i];
num[i]=num[j];
num[j]=temp;
}
}
quick_sort(num,l,j);
quick_sort(num,j+1,r);//注意 l+r/2 对应j与j+1; l+r+1/2对应i与i-1
}
}
import java.util.*;
import java.io.*;
// 请用快速选择算法求出数列从小到大排序后的第 k 个数。首先依照快排的前两步找出i,j,如果k在前半段,则仅对前半段进行快排选择即可,若k在后半段,仅对后半段进行快排选择即可
//在选择后半段时在将k代入时候要减去前半段的长度。快排的时间复杂度为O(nlogn),而此快速选择算法时间复杂度为O(n)
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader reader=new BufferedReader(new InputStreamReader(System.in));
String[] s2=reader.readLine().split(" ");
int n=Integer.parseInt(s2[0]);
int k=Integer.parseInt(s2[1]);
String [] s=reader.readLine().split(" ");
int [] s1=new int[n];
for(int i=0;i<n;i++){
s1[i]=Integer.parseInt(s[i]);
}
System.out.print(quick_select(s1,0,n-1,k));
reader.close();
}
static int quick_select(int[] num ,int s,int e,int k){
if(s==e) return num[s];
int x=num[(s+e)/2];int i=s-1;int j=e+1;
while(i<j){
do i++;while(num[i]<x);
do j--;while(num[j]>x);
if(i<j){
int temp=num[i];
num[i]=num[j];
num[j]=temp;
}
}
int n=j-s+1;
if(k<=n){
return quick_select(num,s,j,k);
}else{
return quick_select(num,j+1,e,k-n);//这里选择后半段,则用k减去前半段的长度
}
}
}
import java.util.*;
import java.io.*;
public class Main{
//归并排序,先递归,后排序,一分为二选取中间值,且需要一个辅助数组,将序列一分为二,分别比较取最小值到辅助数组中,最后使用剩余未比较的部分补全辅助数组再传给原数组
//时间复杂度为O(nlog2n)
public static void main(String[] args) throws IOException{
BufferedReader reader=new BufferedReader(new InputStreamReader(System.in));
int n=Integer.parseInt(reader.readLine());
String [] s=reader.readLine().split(" ");
int [] s1=new int[n];
for(int i=0;i<n;i++){
s1[i]=Integer.parseInt(s[i]);
}
int[] temp=new int[s1.length];
merge_sort(temp,s1,0,n-1);
for(int j=0;j<n;j++){
System.out.print(s1[j]+" ");
}
reader.close();
}
static void merge_sort(int [] temp,int [] num,int s,int e){
if(s>=e){return ;}//递归出口
int mid=(s+e)>>1;//选取中间值
merge_sort(temp,num,s,mid); merge_sort(temp,num,mid+1,e);//先递归
int i=s,j=mid+1,k=0;//确立两个数组的索引以及辅助数组的索引
while(i<=mid&&j<=e){//比较大小填充数组
if(num[i]<=num[j]){
temp[k++]=num[i++];
}else{
temp[k++]=num[j++];
}
}
while(i<=mid){
temp[k++]=num[i++];
}
while(j<=e){
temp[k++]=num[j++];
}
for(int b=s, d=0;b<=e;b++,d++){
num[b]=temp[d];
}
}
}
import java.util.*;
import java.io.*;
public class Main{
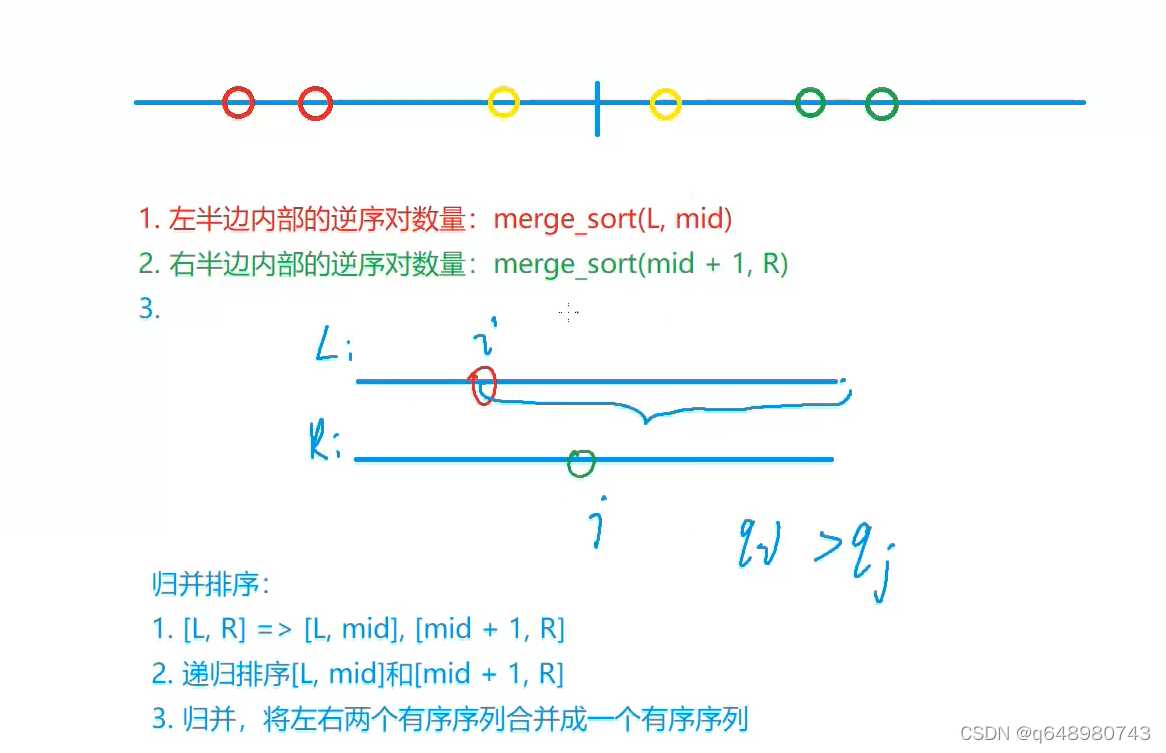
//求逆序对,利用了归并排序从下到上的递归,不断的找分界点拆分小段来求
public static void main(String[] args) throws IOException{
BufferedReader reader=new BufferedReader(new InputStreamReader(System.in));
int n=Integer.parseInt(reader.readLine());
String [] s=reader.readLine().split(" ");
int [] s1=new int[n];
for(int i=0;i<n;i++){
s1[i]=Integer.parseInt(s[i]);
}
int[] temp=new int[s1.length];
System.out.print(merge_sort(temp,s1,0,n-1));
reader.close();
}
static long merge_sort(int [] temp,int[] num,int l,int r){
if(l>=r){
return 0; //给递归的出口;
}
int mid=l+r>>1;
long res=merge_sort(temp,num,l,mid)+merge_sort(temp,num,mid+1,r);//每个merge_sort都会返回该段的逆序对的个数
int k=0;int i=l,j=mid+1;
while(i<=mid&&j<=r){
if(num[i]<=num[j]){
temp[k++]=num[i++];
}else{
temp[k++]=num[j++];
res+=mid-i+1; //因为该段已经排好序,所以只要有num[i]>num[j],大于i的部分全为逆序对,
}
}
while(i<=mid){
temp[k++]=num[i++];//扫尾
}
while(j<=r){
temp[k++]=num[j++];
}
for(int b=l,d=0;b<=r;b++,d++){
num[b]=temp[d];
}
return res;
}
}
|
