?
一、前言
二、顺序表知识点回顾
三、单链表
1.链表的定义
2.单链表的分类
3.单链表尾结点说明
4.单链表基本运算算法
5.快速创建链表
6.循环单链表
四、总结
一、前言
通过上篇文章(线性表中顺序表_m0_50708613的博客-CSDN博客),了解到了数据结构中的线性表有顺序存储和链式存储两种结构,本章主要讲解链式存储结构中单链表和双链表。
二、顺序表知识点回顾
顺序表在逻辑上相邻两个元素在物理上也是相邻的,在存取某一个元素时很容易,而在插入和删除元素时,需要移动大量元素的位置,导致算法的运算量大,时间复杂度大,但是线性表是链式存储结构却可以解决此问题。
顺序表知识点补充——整体创建链表
//整体创建顺序表
void CreateList(SqList &L,ElemType a[],int n)
{
int j=0;
for(int i=0;i<n;++i)
{
L.data[k]=a[i];
j++;
}
L.length=j;
}其时间复杂度为O(n)。
三、单链表
1.链表的定义
每一个结点(node)存放一个数据元素,并用一个指针表示结点间的逻辑结构。如图所示:

date即数据域,用于存放结点(node)的值。
next即指针域或链域,用于存放后继结点的地址。
2.单链表的分类
单链表可分为带头结点和不带头结点两种类型。
3.单链表尾结点说明
单链表的尾结点设计有两种方式
(1)将尾结点的指针域(next)用一个空指针表示,其不指向任何结点,仅仅起到标志作用,故称之为非循环单链表。如图所示:
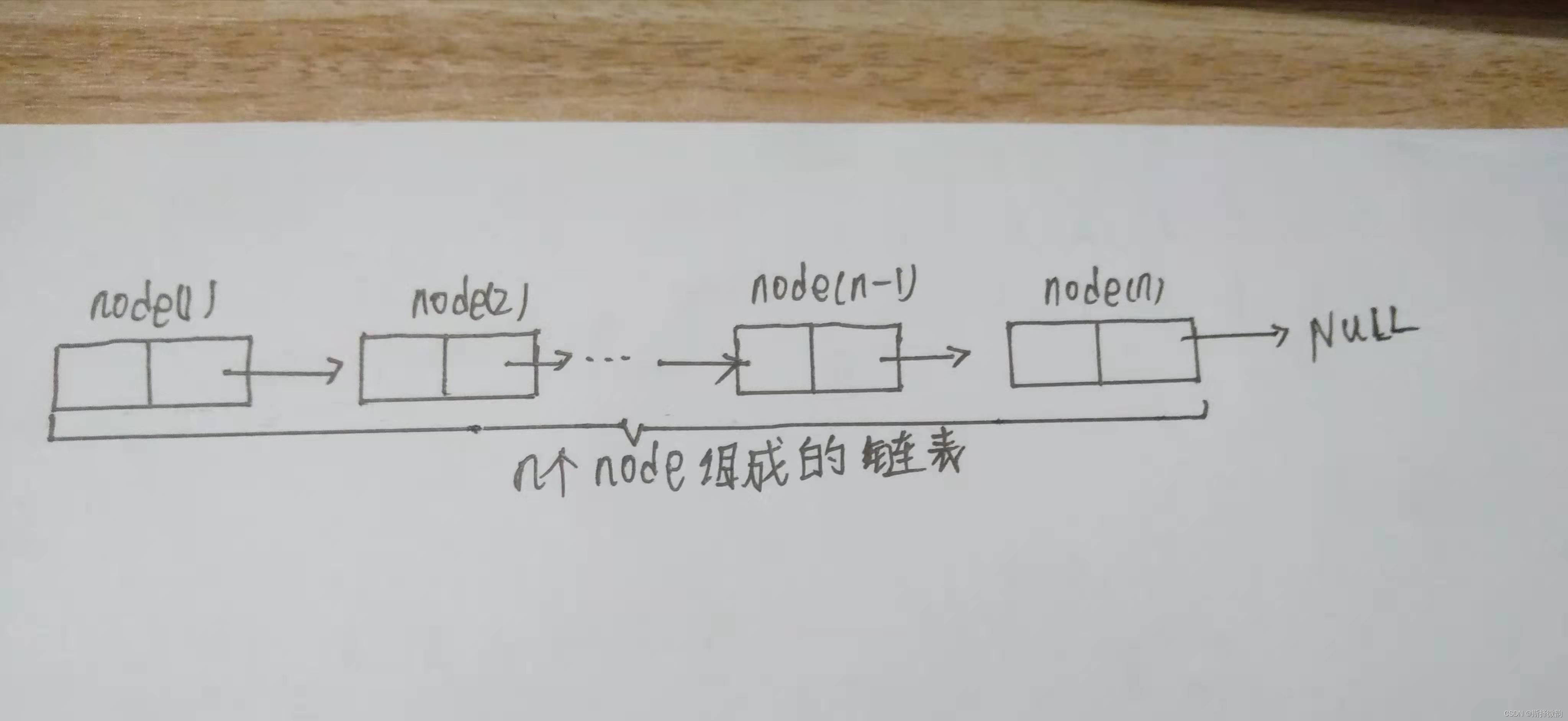
(2)将尾结点的指针域(next)指向头结点,形成环型,也称之为循环单链表。如图所示:
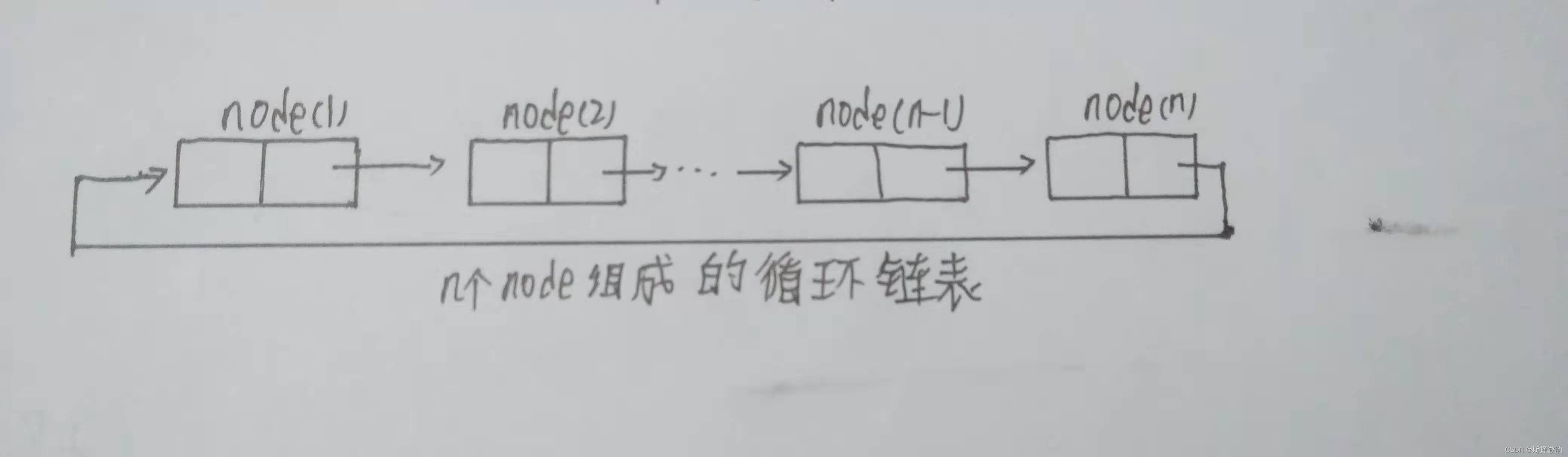
4.单链表基本运算算法
(1)代码详解:
#include <stdio.h>
#include <malloc.h>
//结点类型声明
typedef int ElemType;
typedef struct node
{
ElemType data; //数据域data
struct node *next; //指针域
}LNode; //单链表结点类型
//初始化单链表运算算法
void InitList(LNode *&L) //L为引用型参数
{
L=(LNode*)malloc(sizeof(LNode)); //申请空间,创建头结点L
L->next=NULL; //头结点的指针域(next)指向NULL,表示空链表
}
//销毁单链表的运算算法
void DestroyList(LNode *&L)
{
LNode *p1=L,*p=p1->next;
while(p!=NULL)
{
free(p1); //释放p1结点空间
p1=p;p=p->next; //p1,p同步后移
}
free(p1); //释放p1指向的尾结点空间
}
//求单链表的长度运算算法
int GetLength(LNode *L)
{
int i=0;
LNode *p=L->next; //p指向头结点,i为1
while(p !=NULL)
{
i++;
p=p->next; //p移到下一个结点,i++
}
return i; //p为空时,i即为数据结点个数
}
//求单链表中第i个元素运算算法
int GetElem(LNode *L,int i,ElemType &e)
{
int j=0;
LNode *p=L; //p指向头结点,计数器j值为0
if(i<0)
return 0; //参数i错误返回0
while(p!=NULL && j<i)
{
j++;
p=p->next;
}
if(p==NULL)
return 0; //未找到返回0
else
{
e=p->data;
return 1; //找到后返回1
}
}
//按值查找运算算法
int Locate(LNode *L,ElemType e)
{
LNode *p=L->next;
int j=1; //p指向头结点,j置为序号1
while(p!=NULL && p->data!=e)
{
p=p->next;
j++;
}
if(p==NULL)
return(0); //未找到返回0
else
return (j); //找到后返回其序号
}
//插入元素运算算法
int InsElem(LNode * &L,ElemType x,int i) //插入结点值为X的结点
{
int j=0;
LNode *p=L,*s;
if(i<=0)
return 0; //参数i错误返回0
while(p!=NULL && j<i-1) //查找第i-1个结点p
{
j++;
p=p->next;
}
if(p==NULL)
return 0; //未找到第i-1个结点是返回0
else //找到第i-1个结点p
{
s=(LNode*)malloc(sizeof(LNode));
s->data=x; //创建存放元素x的新结点s
s->next=p->next; //将s结点插入到P结点之后
p->next=s;
return 1; //插入成功,返回1
}
}
//删除结点运算算法
int DelElem(LNode *&L,int i)
{
int j=0;
LNode *p=L,*q;
if(i<=0)
return 0; //参数i错误返回0
while(p!=NULL && j<i-1) //查找第i-1个结点
{
j++;
p=p->next;
}
if(p==NULL)
return 0; //未找到第i-1个结点是返回0
else //找到第i-1个结点p
{
q=p->next; //q指向被删除的结点
if(q==NULL)
return 0; //没有第i个结点是返回0
else
{
p->next=q->next; //从单链表中删除q结点
free(q); //释放其空间
return 1;
}
}
}
//输出单链表
void DispList(LNode *L)
{
LNode *p=L->next;
while(p!=NULL)
{
printf("%d",p->data);
p=p->next;
}
printf("\n");
}
void main()
{
int i;
ElemType e;
LNode *L;
InitList(L);
InsElem(L,6,1);
InsElem(L,4,2);
InsElem(L,4,3);
InsElem(L,7,4);
InsElem(L,1,5);
InsElem(L,9,6);
InsElem(L,8,7);
InsElem(L,3,8);
InsElem(L,2,9);
InsElem(L,7,10);
printf("单链表: ");
DispList(L);
printf("长度: %d\n",GetLength(L));
i=6;
GetElem(L,i,e);
printf("第%d个元素: %d\n",i,e);
e=3;
printf("元素%d是第%d个元素\n",e,Locate(L,e));
i=7;
printf("删除第%d个元素\n",i);
DelElem(L,i);
printf("单链表:");
DispList(L);
DestroyList(L);
}(2)结果演示
(3) 单链表基本运算算法时间复杂度分析
| 基本运算算法 | 时间复杂度 |
| void InitList(LNode *&L)——初始化 | O(1) |
| void DestroyList(LNode *&L)——销毁 | O(n) |
| int GetLength(LNode *L)——求单链表的长度 | O(n) |
| 求单链表中第i个元素 int GetElem(LNode *L,int i,ElemType &e) | O(n) |
| int Locate(LNode *L,ElemType e)——查找 | O(n) |
| int InsElem(LNode * &L,ElemType x,int i) ——插入 | O(n) |
| int DelElem(LNode *&L,int i)——删除 | O(n) |
| void DispList(LNode *L)——输出单链表 | O(n) |
5.快速创建链表
a:头插法
#头插法
void CreateListF(LNode *&L,ElemType a[],int n)
{
LNode *s;
L=(LNode*)malloc(sizeof(LNode)); //申请空间
L->next=NULL; //创建一个空单链表
for(int i;i<n;i++) //遍历a[]所有元素
{
s=(LNode*)malloce(sizeof(LNode));
s->data=a[i]; //将创建存放a[i]元素的新节点s
s->next=L->next; //将s结点插入到头结点
L->next=s;
}
}注:建成 的单链表结点次序与插入次序相反。
b:尾插法
//尾插法
void CreateListR(LNode *&L,ElemType a[],int n)
{
LNode *s,*d;
L=(LNode *)malloc(sizeof(LNode)); //创建头结点
d=L; //d始终指向尾结点,初始时指向头结点
for(int i=0;i<n;++i)
{
s=(LNode *)malloc(sizeof(LNode));
s->data=a[i]; //创建存放a[i]元素的新节点s
d->next=s;
d=s; //结点s变成新的尾结点,
}
d->next=NULL; //由于是普通的单链表,故尾结点next域置为NULL
}注:建成 的单链表结点次序与插入次序相同。
6.循环单链表
循环单链表与普通单链表非常相似,只是将单链表中尾结点的next域有原来的NULL改为指向头结点,其基本运算算法极其相似。下面给出循环单链表的基本运算算法。
typedef int ElemType;
//类型声明
typedef struct node
{
ElemType data;
struct node *next;
}LNode;
//初始化循环单链表运算算法
void InitList(LNode *&L)
{
L=(LNode*)malloc(sizeof(LNode));
L->next=L; //尾结点指向头结点,不再指向NULL
}
//销毁循环单链表运算算法
void DestroyList(LNode *&L)
{
LNode *p1,*p=p->next;
while(p1!=L)
{
free(p1);
p1=p;
p=p->next;
}
free(p1);
}
//求循环单链表的长度运算算法
int GetLength(LNode *L)
{
int i=0;
LNode *p=L->next;
while(p!=L)
{
i++;
p=p->next;
}
return i;
}
//求循环单链表中第i个元素运算算法
int GetElem(LNode *L,int i,ElemType &e)
{
int j=1;
LNode *p=L->next;
if(i<=0)
return 0;
while(p!=L && j<i)
{
j++;
p=p->next;
}
if(p==L)
return 0;
else
{
e=p->data;
return 1;
}
}
//按值查找运算算法
int Locate(LNode *L,ElemType x)
{
int i=1;
LNode *p=L->next;
while(p!=L && p->data!=x) //从头结点开始查找data域为x的结点
{
p=p->next;
i++;
}
if(p==L)
return 0; //未找到值为x的结点返回0
else
return i; //找到第一个值为x的结点并返回i
}
//插入元素运算算法
int InsElem(LNode *&L,ElemType x,int i)
{
int j=1;
LNode *p1=L,*p=p1->next,*s;
if(i<=0)
return 0; //参数i错误返回0
while(p!=L && j<i) //查找第i个结点p和其前驱结点
{
j++;
p1=p;
p=p->next;
}
if(p==L && i>j+1)
return 0; //参数i>n+1是错误返回0
else //成功查找到底i个结点是前驱结点
{
s=(LNode*)malloc(sizeof(LNode));
s->data=x;
s->next=p1->next;
p1->next=s;
return 1;
}
}
//删除运算算法
int DelElem(LNode *&L,int i)
{
int j=0;
LNode *p=L,*p2; //p指向头结点
if(i<=0)
return 0; //参数i错误返回0
while(p->next !=L && j<i-1) //查找第i-1个结点p
{
j++;
p=p->next;
}
if(p->next==L)
return 0; //未找到返回0
else
{
p2=p->next; //p2指向被删结点
if(p2==L)
return 0; //没有第i个结点是返回0
else
{
p->next=p2->next; //从循环单链表中删除p2结点
free(p2); //释放其空间
return 1; //成功删除返回1
}
}
}
//输出循环单链表运算算法
void DispList(LNode *L)
{
LNode *p=L->next;
while(p!=L)
{
printf("%d",p->data);
p=p->next;
}
printf("\n");
}四、总结
单链表的物理存储位置是随机的,没有一一对应的逻辑关系,在插入和删除运算时,必备大量的移动数据域的位置,只要设计一个新指针进行遍历便好。而且创建链表有两种快速的方法,可选择性提高了,可根据情况选择对应的方法创建链表解决问题。
