一致性Hash算法的应用领域

对于一致性Hash算法而言，我们可以在很多地方看到它的身影：

Redis
Nginx
Dubbo
ElasticSearch
Hadoop
分布式数据库
其他分布式数据存储场景…

详解一致性Hash算法

以缓存为例子，我们一起思考为什么一致性Hash算法频繁的被用于如上种种场景，对于以往高并发场景，我们通常的处理方式如下：

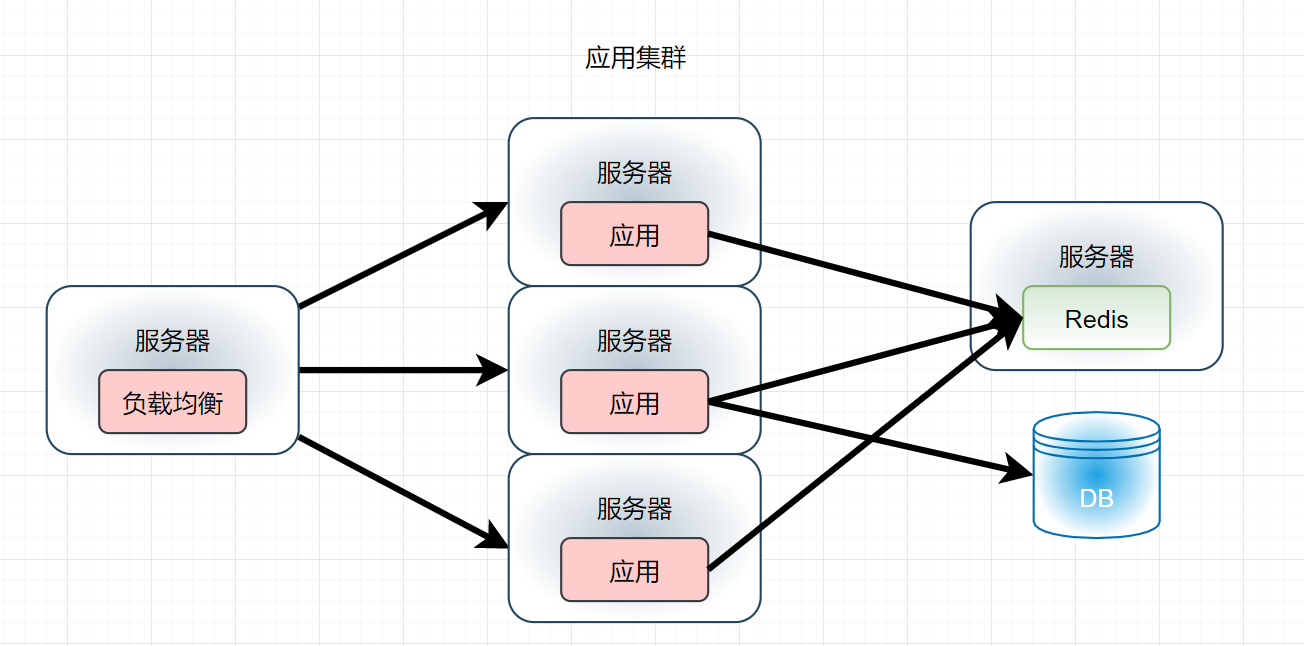
对于Redis的10W并发能力，大家应该也很清楚，但是如果并发量达到了30W呢？但就这一点，我们并不难解决，因为我们既然应用可以增加集群，那么缓存一样可以增加分布式的缓存集群：

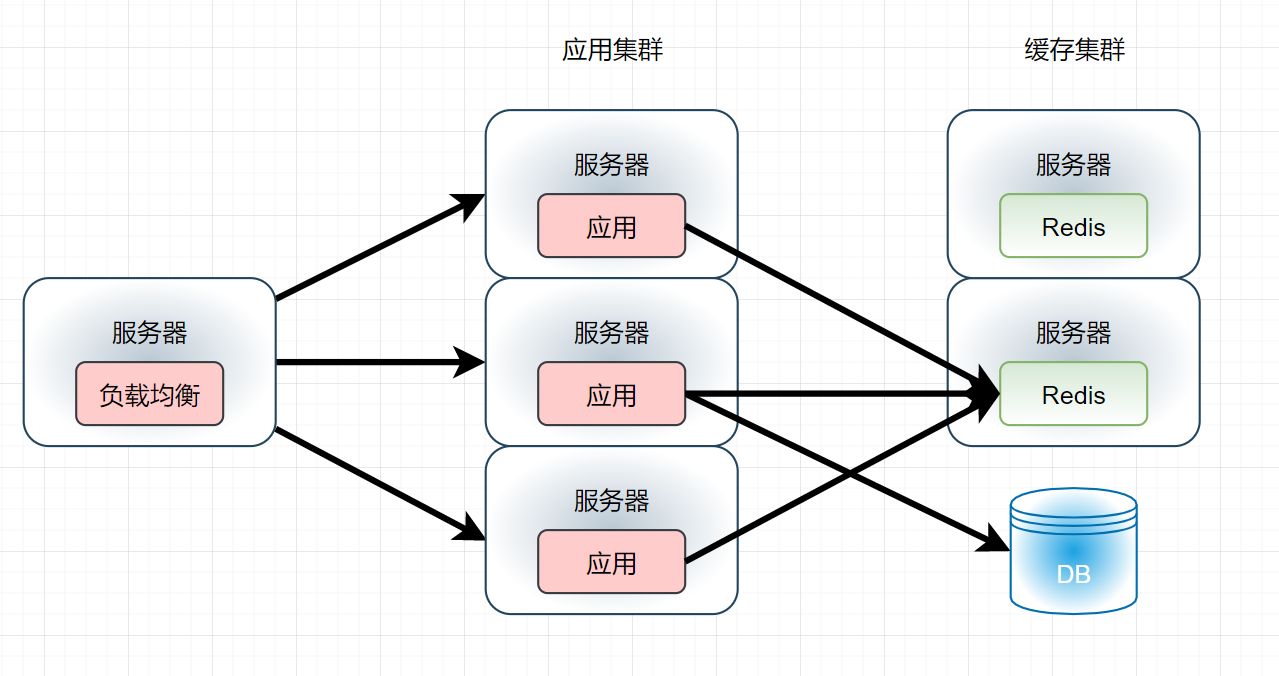
但是真的有这么简单吗？首先思考一个问题，对于海量的缓存数据，已经超出了一台单机缓存服务器的内存容量的时候，怎么办？答案理所当然应该是：将海量的数据划分成若干部分，分别将其缓存到每一台缓存服务器上面。接着再思考一个问题，对于海量的数据，我们如何才能让其均衡的分布在缓存集群的每一个节点上呢？如果不让其均衡的分布到各个节点上，总是让大批量的缓存集中的存储在某一台缓存服务器上面，那我们部署缓存集群的目的在哪里？

hash(key)%集群节点数

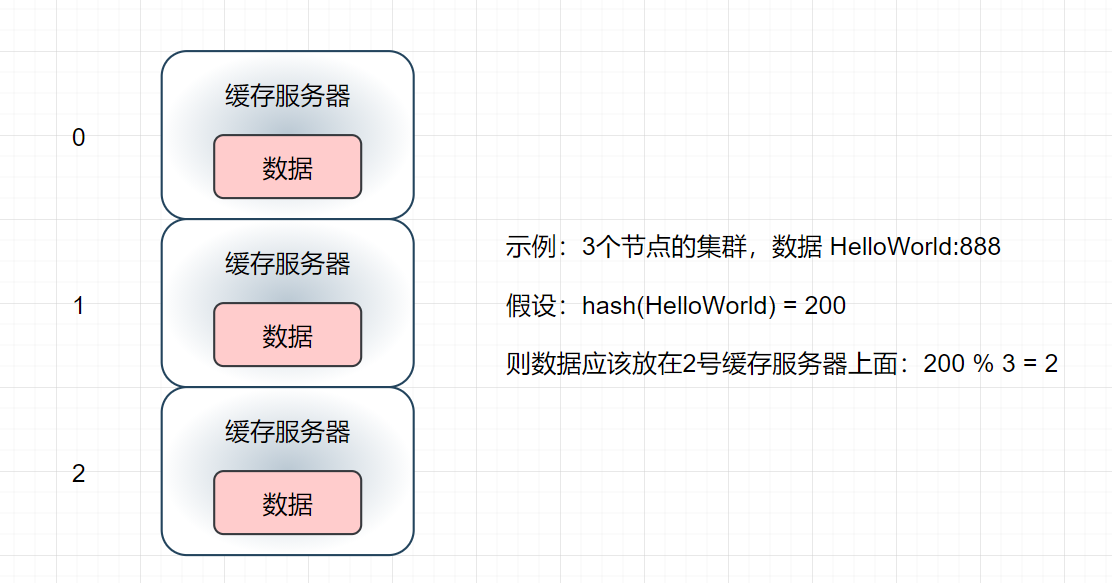
这种方案会存在一个问题，当我们由于业务需要，临时决定增加一个服务器来提高集群性能，会不会影响到原始的缓存数据呢？

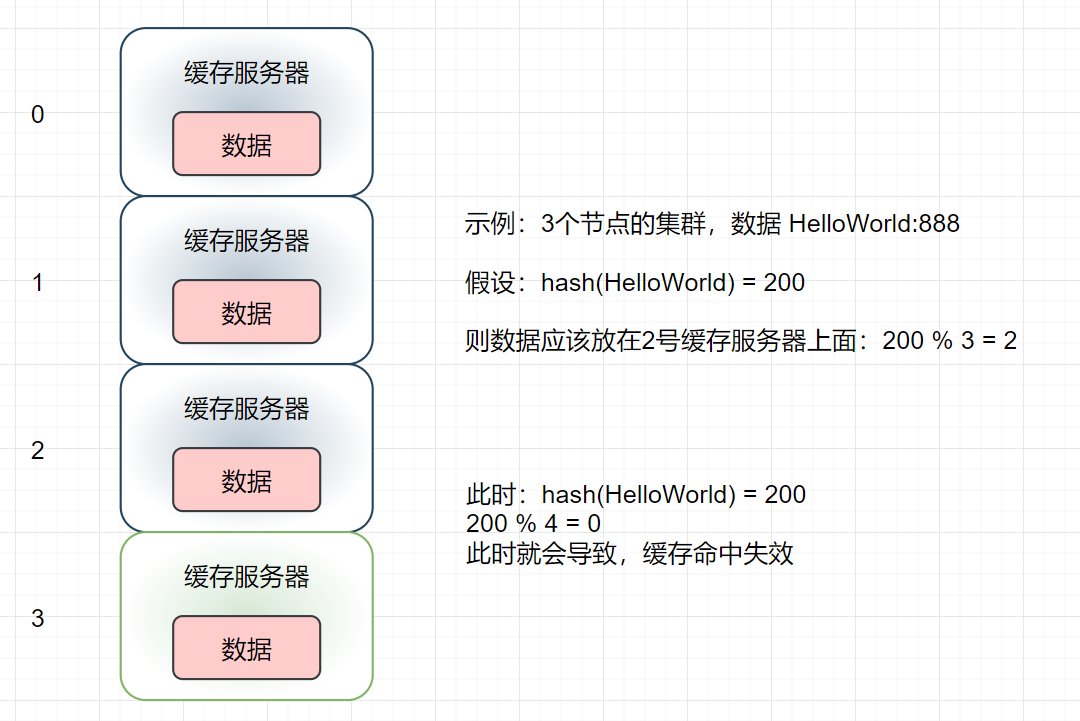
经过简单计算，当原本的3台缓存服务器增加到4台后，我们将会有3/4的缓存数据将会失效，同理，如果原本缓存服务器就有99台，此时将其扩容至100，那么将会有99/100的缓存数据将会失效！这是在生产环境中不能接收的结果，大量的缓存失效，大量的请求直接访问数据库，这一幕不正是缓存雪崩所带来的后果吗？

一致性Hash算法

一致性Hash环

首先给出一致性Hash的部分特点，其中max = 2³²-1，也就是int的最大值

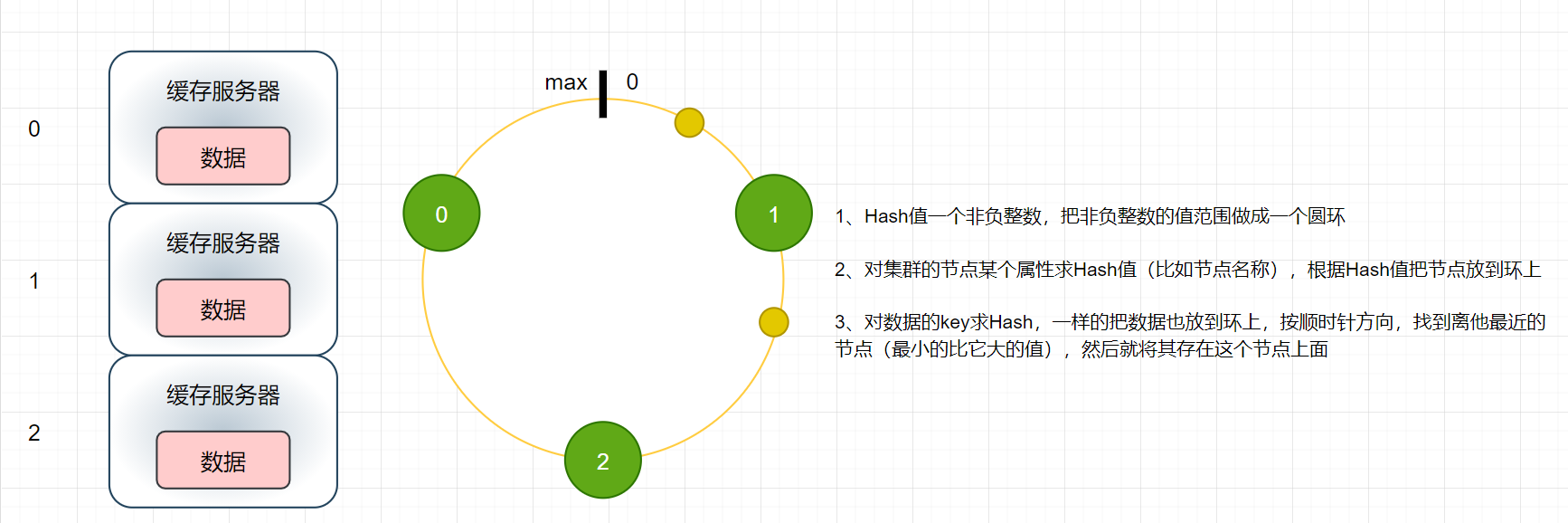
同样的问题，我们此时增加一台缓存服务器，会对原始缓存有什么影响？

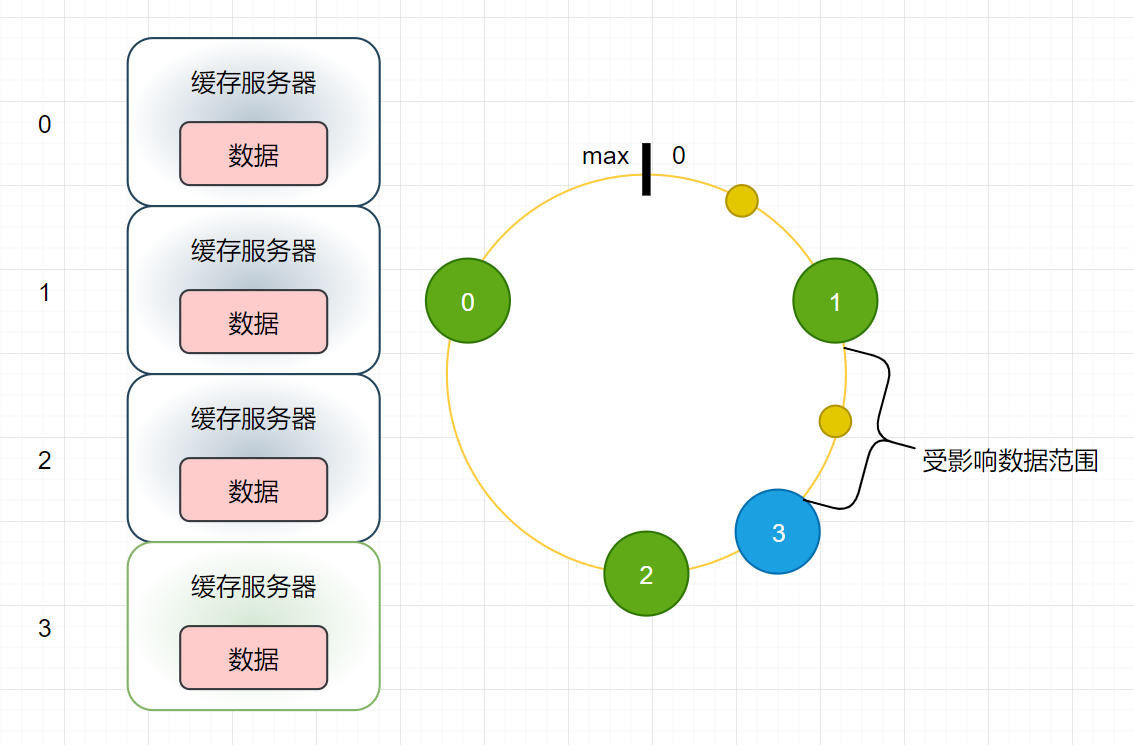
很容易推导，受影响的数据范围和新增节点与上一个节点之间的差值有关，很容易就能对比出来，这点误差对比以前的纯Hash求余，已经小很多了

现在开始思考两个问题，新增的节点能够均衡环节原有节点的压力吗？集群的节点一定会均衡分布在环上面吗？
对于第一个问题，答案是不能，比如上图中的3号，它只能分担来自2号服务器的压力，但是并不能分担0和1号的压力
对于第二个问题，答案也是不能，因为图中只是展示出了一种理想的条件下，真实根据服务属性求出的hash值并不会严格的均匀

虚拟节点

为了解决上述两个问题，引入虚拟节点的概念：

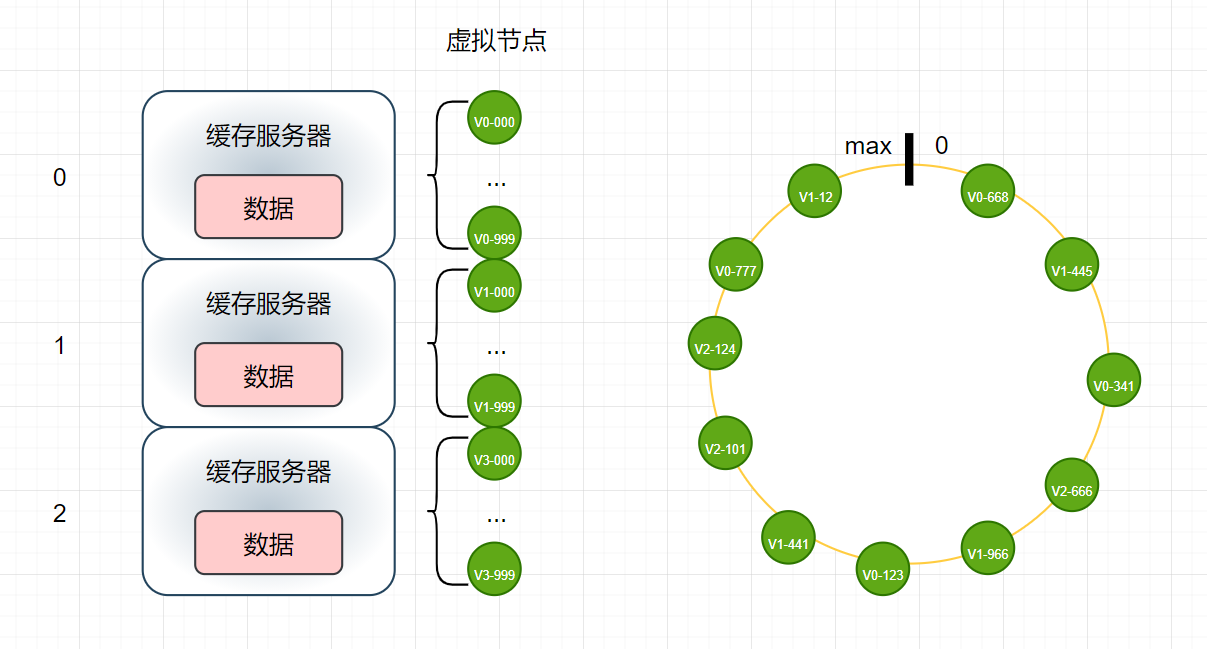
此时再增加一个缓存服务器：

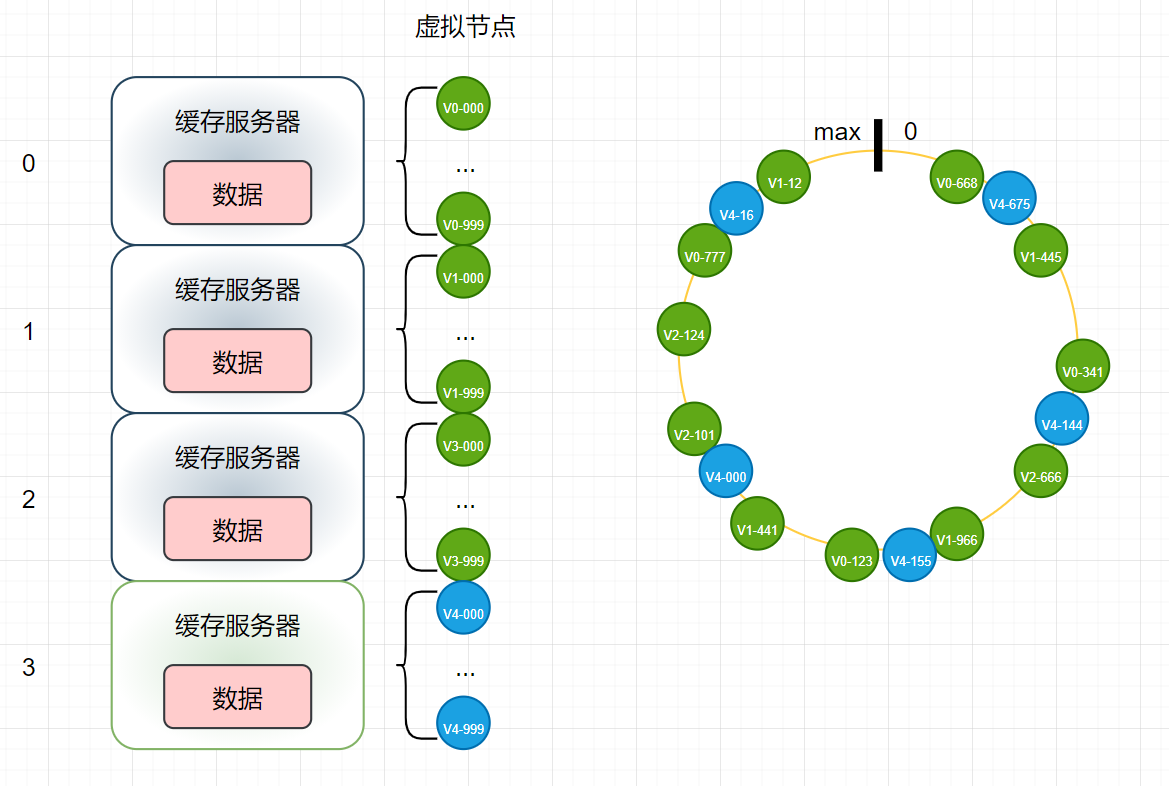
看图很明显得出结论：虚拟节点越多，分布便越均衡（第一个问题），新增的节点对原有节点的影响就越均衡（第二个问题），更进一步可以算出新增节点后，缓存失效的比例将只有1/n（n表示原有服务器数）

如果你有了解过Redis分布式缓存，那么你会知道其中一个哈希槽的概念，其中内置的哈希槽的数量有16384个(2¹⁴)，其本质，仍然是虚拟节点，只不过这个哈希槽是一开始就划分完毕了，当只有一个节点，会将所有的哈希槽分配给它，如果新增了一个节点，会将原有的节点中转移出一半，如果继续再增加一个，那么就会在原有的两个节点中转移三分之一的槽位出来，以此类推

手写一个一致性Hash算法

在实现一致性Hash算法之前，还是先回顾一下我们需要做的有哪些：

物理节点
虚拟节点
Hash算法，Java默认提供的HashCode方法得到的hash值散列度不是很好，而且会有负值（可以取绝对值），市面上的Hash算法也有很多，比如：CRC32_HASH，FNV1_32_HASH，KETAMA_HASH（MemCache推荐的一致性Hash算法），咱们这里采用FNV1_32_HASH算法

private static int getHash(String string) {
    final int p = 16777619;
    int hash = (int) 2166136261L;
    for (int i = 0; i < string.length(); i++) {
        hash = (hash ^ string.charAt(i)) * p;
    }
    hash += hash << 13;
    hash ^= hash >> 7;
    hash += hash << 3;
    hash ^= hash >> 17;
    hash += hash << 5;
    return hash < 0 ? Math.abs(hash) : hash;
}

一致性Hash环，我们顺时针看的话，其实就是一个排序的集合，而且往里加节点的时候，也要保证原有集合有序（可以延申出对于排序的数据集合，查找元素最快就是用二分查找），这时候采用什么数据结构呢？数组，对插入不太友好，链表，无法实现二分查找，树呢？答案就是红黑树，这时候就需要借助集合框架中的TreeMap，它底层就是采用红黑树实现！
虚拟节点如何放到环上
数据如何找到对应的虚拟节点

完整代码如下：

import lombok.Data;

import java.util.*;

/**
 * @author PengHuanZhi
 * @date 2022年01月15日 17:08
 */
@Data
public class ConsistenceHash {
    /**
     * 虚拟节点数量
     **/
    private int virtualNums = 100;
    
    /**
     * 物理节点
     **/
    private List<String> realNodes = new ArrayList<>();

    /**
     * 对应关系
     **/
    private Map<String, List<Integer>> real2VirtualNodeMap = new HashMap<>();

    /**
     * 一致性Hash环
     **/
    private SortedMap<Integer, String> hashRing = new TreeMap<>();

    /**
     * 加服务器
     *
     * @param node 真实节点
     **/
    public void addServer(String node) {
        realNodes.add(node);
        //虚拟出多少个虚拟节点
        String visualNode;
        List<Integer> virNodes = new ArrayList<>(virtualNums);
        real2VirtualNodeMap.put(node, virNodes);
        for (int i = 0; i < virtualNums; i++) {
            visualNode = node + "-" + i;
            //放到环上
            //1、求Hash值，由于Java默认提供的HashCode方法得到的hash值散列度不是很好，所以我们采用新的HashCode算法
            int hash = getHash(visualNode);
            //2、放到环上去
            hashRing.put(hash, node);
            //3、保存对应关系
            virNodes.add(hash);
        }
    }

    /**
     * 找到数据的存放节点
     *
     * @param virtualNode 虚拟节点key
     * @return 返回真实节点
     */
    public String getServer(String virtualNode) {
        int hashValue = getHash(virtualNode);
        SortedMap<Integer, String> subMap = hashRing.tailMap(hashValue);
        if (subMap.isEmpty()) {
            //数据应该放在最小的节点
            return hashRing.get(hashRing.firstKey());
        }
        return subMap.get(subMap.firstKey());
    }

    /**
     * 移除节点
     *
     * @param node 节点名称
     **/
    public void removeNode(String node) {
        realNodes.remove(node);
        real2VirtualNodeMap.remove(node);
        String visualNode;
        for (int i = 0; i < virtualNums; i++) {
            visualNode = node + "-" + i;
            int hash = getHash(visualNode);
            hashRing.remove(hash);
        }
    }

    /**
     * FNV1_32_HASH算法
     *
     * @param string key
     * @return int 返回Hash值
     **/
    private static int getHash(String string) {
        final int p = 16777619;
        int hash = (int) 2166136261L;
        for (int i = 0; i < string.length(); i++) {
            hash = (hash ^ string.charAt(i)) * p;
        }
        hash += hash << 13;
        hash ^= hash >> 7;
        hash += hash << 3;
        hash ^= hash >> 17;
        hash += hash << 5;
        return hash < 0 ? Math.abs(hash) : hash;
    }
}