[数据结构与算法]数据结构-线性表及顺序结构

线性表的定义

由n(n$?$ 0)个数据元素(结点)a₁,a₂,…a_n,组成的有限序列

• 其中数据元素的个数n定义为表的长度
• 当n=0时称为空表
• 将非空的线性表记作：(a₁,a₂,...a_n)
• 这里的数据元素a_i(1?i?n )只是一个抽象的符号，其具体含义在不同的情况下可以不同
• 
  

  线性表的逻辑特征

  • 在非空的线性表，有且仅有一个开始的节点a₁,它没有直接前趋，而仅有一个直接后继a₂;
  • 有且仅有一个终端节点a_n,它没有直接后继，而仅有一个直接前趋a_n-1;
  • 其余内部节点a_i(2$?$i$?$n-1)都有且仅有一个直接前趋a_i-1和一个直接后继a_i+1
    
    PS:<a_i,a_i+1>，a_i是a_i+1的前趋，a_i+1是a_i的后继。
    线性表是一种典型的线性结构
    

  抽象数据类型线性表的定义

  ADT List{
  ??? ~~~ ??? 数据对象：D={a_i | a_i属于Elemset,(i=1,2,…,n,n$?$ 0) }
  ??? ~~~ ??? 数据关系：R={<a_i-1,a_i>|a_i-1,a_i属于D，(i=2,3,…,n)
  ??? ~~~ ??? 基本操作
  }ADT List

  线性表的顺序储存表示

  线性储存的表示又称为顺序储存结构或顺序映像
  顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构
  
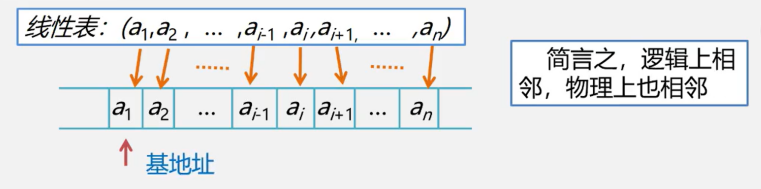
  线性表的第一个数据位置a₁的存储位置，称为线性表的起始位置或基地址。
  
  线性表顺序结构占用一片连续的存储空间。知道某个元素的存储位置就可以计算其他元素的位置。
  假设线性表的每个元素占l个存储单元，则l+1个数据元素的存储位置和第i个数据的存储位置之间满足关系：

  LOC(a_i+1) = LOC(a_i) + l 由此，所有数据元素的存储位置均可由第一个数据元素的存储位置得到： LOC(a_i) = LOC(a₁) + (i-1) X l PS:LOC()表示存储地址
  逻辑位序和物理位序相差1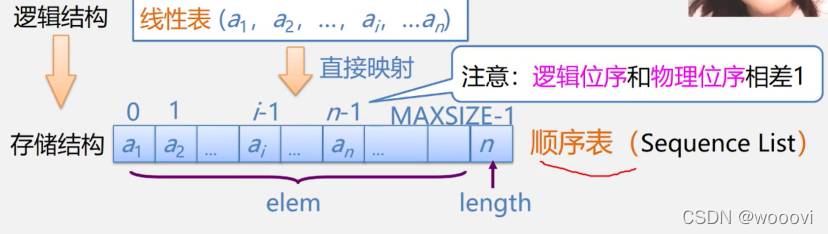

  

  补充

  数组定义

  数组静态分配

  typedef struct
  {
      ElemType data[MaxSize];
      int length;
  }Sqlist;//顺序表类型
  

  数组动态分配

  typedef struct
  {
      ElemType *data;
      int length;
  }Sqlist;//顺序表类型
  

  C语言的内存动态分配

  Sqlist L;
  l.data = (ElemType*)malloc(sizeof(ElemType)*MaxSize)
  

  • malloc(m)函数，开辟m字节长度的地址空间，并返回这段地址的首地址
  • sizeof(x)函数，计算变量x的长度
  • free§函数，释放指针p所指变量的存储空间，即彻底删除一个变量。

  需要加载头文件：<stdlib.h>

  C++动态存储分配

  new 类型名（初值列表）
  ?? ~~ ??功能：
  ???? ~~~~ ????申请用于存放T类型对象的内存空间，并依初值列表赋以初值结果值：
  ???? ~~~~ ????成功：T类型的指针，指向新分配的内存
  ???? ~~~~ ????失败：0（NULL）
  
  

  delete 指针p
  ?? ~~ ??功能：
  ???? ~~~~ ????释放指针p所指向的内存。p必须是new操作的返回值。

  基本操作

  顺序线性表的定义模板：

  #define LIST_INIT_SIZE 100 //线性表存储位置的初始分配量
  typedef struct 
  {
      ElemType elem[LIST_INIT_SIZE];
      int length;//当前长度
  }SqList;
  
  

  补充：操作算法中用到的预定义常量和类型

  //函数结果状态码
  #define TURE 1
  #define FALSE 0
  #define OK 1
  #define ERROR 0
  #define INFEASIBLE -1
  #define OVERFLOW -2
  //Status 是函数的类型，其值是函数结果的状态码
  typedef int Status;
  typedef char ElemType;
  

  • InitList(&L)
    • 操作结果：构造一个空的线性表L

  Status InitList Sq(SqList &L){
  	L.elem = new ElemType[MAXSIZE];
  	if(!=L.elem) exit(OVERFLOW);
  	L.length = 0;
  	return OK;
  }
  

  • DestoryList(&L)
    • 初始条件：线性表L已经存在。
    • 操作结果：销毁线性表L。

  void DestroyList(SqList &L){
      if (l.elem)delete L.elem;//释放存储空间
  }
  

  • ClearList(&L)
    • 初始条件：线性表L已经存在。
    • 操作结果：将线性表L重置为空表。

  void ClearList(SqList &L){
      L.length = 0;//将线性表的长度置为0
  }
  

  • ListEmpty(L)
    • 初始条件：线性表L已经存在。
    • 操作结果：若线性表L为空表，则返回TURE;否则返回FLASE。

  int IsEmpty(SqList L){
      if(L.length == 0)return 1;
      else return 0;
  }
  

  • ListLength(L)
    • 初始条件：线性表L已经存在。
    • 操作结果：返回线性表L中数据元素的个数。

  int GetLength(SqList L){
      return (L.length);
  }
  

  • GetElem(L,i,&e)
    • 初始条件：线性表L已经存在,1$?$i$?$ListLength(L)。
    • 操作结果：用e返回线性表L中第i个数据元素的值。

  int GetElem(SqList L,int i,ElemType &e){
      if(i<1||i>L.length) return ERROR;
      //判断i值是否合理，若不合理，则返回ERROR
      e = L.elem[i-1];
      return OK;
  }
  

  • LocateElem(L,i,&e)
    • 初始条件：线性表L已经存在,compare是数据元素判定的函数。
    • 操作结果：返回线性表L中第1个与e满足compare()的数据元素的位序。若这样的数据元素不存在则返回值为0

  int LocalElem(SqList L,ElemType e){
      for(i=0;i<L.length;i++)
          if(L.elem[i]==e) return i+1;//查找成功，返回序号
      return 0;//查找失败，返回0
  }
  

  • PriorElem(L,cur_e,&pre_e)
    • 初始条件：线性表L已经存在。
    • 操作结果：若cur_e是L的数据元素，且不是第一个，则用pre_e返回它的前驱，否则操作失败；pre_e无意义。
  • NextElem(L,cur_e,&next_e)
    • 初始条件：线性表L已经存在。
    • 操作结果：若cur_e是L的数据元素，且不是最后一个，则用next_e返回它的前驱，否则操作失败；next_e无意义。
  • ListInsert(&L,i,e)
    • 初始条件：线性表L已经存在,1$?$i$?$ListLength(L)+1。
    • 操作结果：在L的第i个位置插入新的数据元素e，L的长度加一。

  Status ListInsert_Sq(SqList &L,int i,ElemType e){
      if(i<1||i>L.length+1)return ERROR;//i值不合法
      if(L.length==MAXSIZE)return ERROR;//当前存储空间已满
      for(j=L.length-1;j>=i-1;j++)
          L.elem[j+1] = L.elem[j]//插入位置及之后的元素后羿
      L.elem[i-1]=e;//将新元素e放入第i个位置
      L.length++;//表长增1
      return OK;
  }
  

  • ListDelete(&L,i,&e)
    • 初始条件：线性表L已经存在,1$?$i$?$ListLength(L)。
    • 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减一。

  Status ListDelete_Sq(SqList &L,int i){
      if(i<1||i>L.length)return ERROR;//i值不合法
      for(j=i;j<=L.length-1;j++)
          L.elem[j-1] = L.elem[j]//被删除元素之后的元素前移
      L.length--;//表长减1
      return OK;
  }
  

  • ListTraverse(&L,i,visited())
    • 初始条件：线性表L已经存在,1$?$i$?$ListLength(L)。
  • 操作结果：依次对线性表中每个元素调用visited()。

  顺序表优缺点

  优点

  • 存储密度大（结合本身所占存储量/结点结构所占存储量）
  • 可以随机存取表中任一元素

  缺点

  • 在插入、删除某一元素时，需要移动大量元素
  • 浪费存储空间
  • 属于静态存储形式，数据元素的个数不能自由扩充

  欢迎您的关注
  如有转载，请注明出处（如不注明，盗者必究）