[数据结构与算法]美赛python学习d5--线性规划

线性规划

线性规划的目的

确定多变量线性函数在变量满足线性约束条件下的最优值
线性规划模型需要确定的三个要素

1. 决策变量
2. 目标函数：决策者希望对其优化的指标，是决策变量的线性函数
3. 约束条件：决策变量取值的限制范围

线性规划的一般模型

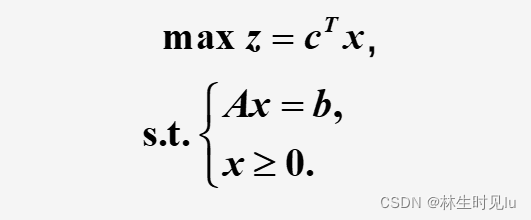
线性规划模型最优解的情况

1. 有唯一最优解
2. 有无穷多个最优解
3. 无可行解
4. 有可行解但目标函数非空

线性规划的python 求解

运用scipy.optimize模块中的linprog函数求解

1. 将线性规划问题化为scipy中线性规划模型的标准型
   注意标准型中都是最小值，若原来要求最大值也需要将表达式取反求最小
   
   

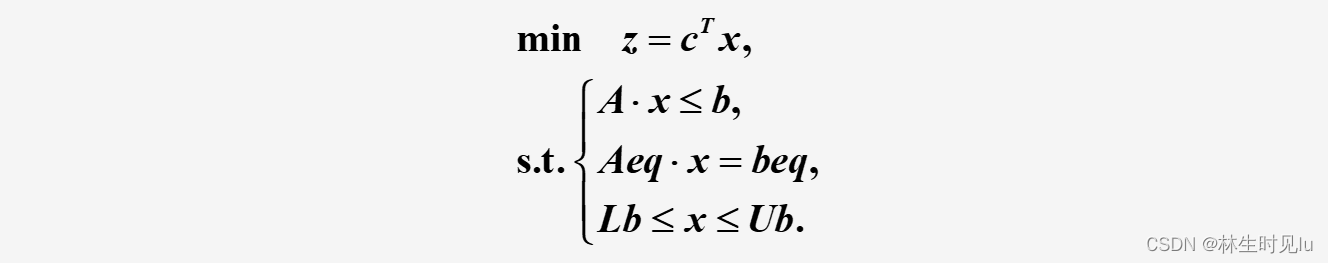
2. 实例
   
   

• python zip函数
  zip函数将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组
  

灵敏度分析

在上述线性规划求解问题中我们假设$a_{ij}$,$b_i$,$c_j$是常数，是固定不变的，但是在实际问题中，由于生产工艺的变化，这些参数往往是预测值或估计值，经常会有少许的变化，由此我们可以考虑由于参数变化导致的现行最优解的变化，讨论将这些参数的变化限制在什么范围内，原最优解仍然是最优的。

整数规划

在实际问题中，决策变量代表产品的件数，箱数，人员的个数等整数量时，变量只有取整数才有意义，因此有必要在规划模型中增加这些决策变量为整数的限制

标准指派问题的模型及求解

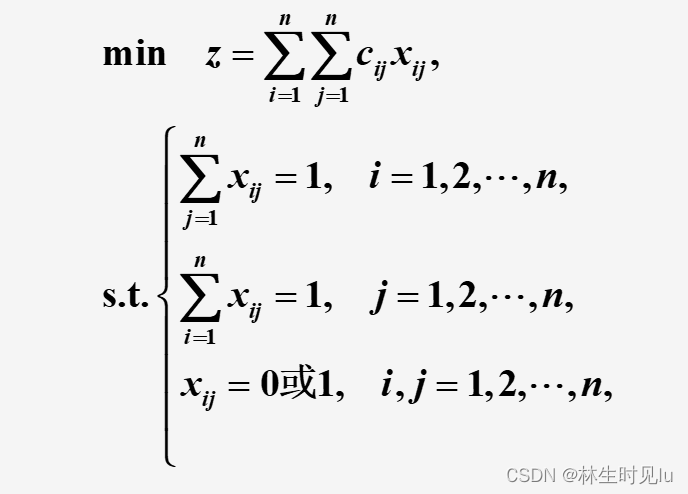
装箱问题

非线性规划问题

非线性规划问题与线性规划问题的区别在于，非线性规划可能的目标函数和约束条件可能不都是线性的
非线性规划问题可以有约束条件也可以没有约束条件，非线性规划的一般模型描述如下

1. 用scipy.optimize模块的minimize函数求解