[数据结构与算法]力扣5982——解决智力问题（动态规划，正序dp、倒序dp）

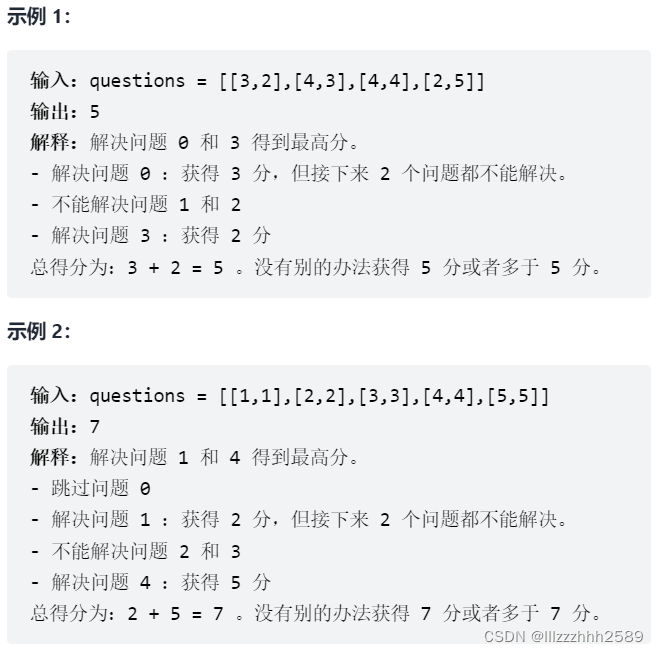
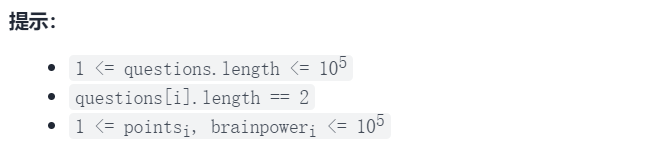
思路，倒序

类似背包选取的问题，但要求有选取间隔
由于数据量比较大，回溯的选取很容易超时。

第一种方法，倒序的更新dp，正向想的难点在于，对于新的位置，不知道前面限制要跳过多少，如果记录需要多一重循环超时。
倒序的想，就可以在每次选择的时候知道跳过多少位置，因为对当前要处理的元素i来说，可以知道如果取了该位置要跳过brainpower[i]个问题，可由后面位置更新当前位置，转移方程转自大佬灵茶山艾府

代码

class Solution {
public:
    long long mostPoints(vector<vector<int>>& q) {
        int n = q.size();
        long long ans = 0;
        vector<long long> dp(1e6, 0);
        for(int i = n-1; i >= 0; i--) {
            dp[i] = max(dp[i+1], q[i][0] + dp[i+q[i][1]+1]);
        }
        return dp[0];       
    }
};

思路，正序

对于每个位置，更新选择和不选的next位的dp；
如果不选择当前位i，next位为i+1，更新dp[next]；
如果选择当前位i，next位为跳过限制后的i + questions[i][1] + 1，更新next；

遍历，对每个位置更新他的两种方式的next位，最后dp数组中最大值就是答案。

状态转移方程转自大佬灵茶山艾府

代码

class Solution {
public:
    long long mostPoints(vector<vector<int>>& questions) {
        int n = questions.size();
        vector<long long> dp(1e6, 0);
        for(int i = 0; i < n; i++) {
            int next = i + 1;   //不选
            dp[next] = max(dp[next], dp[i]);
            next = i + questions[i][1] + 1;
            dp[next] = max(dp[next], (long long)questions[i][0] + dp[i]);
        }
        return *max_element(dp.begin(), dp.end());
        
    }
};

另外，对于 i=n-1和 next≥n 的情况，可以将其更新到 dp[n] 中，避免最后一次的遍历找最大值

class Solution {
public:
    long long mostPoints(vector<vector<int>>& questions) {
        int n = questions.size();
        vector<long long> dp(n + 1, 0);
        for(int i = 0; i < n; i++) {
            int next = i + 1;   //不选
            dp[next] = max(dp[next], dp[i]);
            next = min(i + questions[i][1] + 1, n); //选择当前位，跳过
            dp[next] = max(dp[next], (long long)questions[i][0] + dp[i]);
        }
        return dp[n];
    }
};