[数据结构与算法]【剑指offer】＜树--中等＞【JZ86 在二叉树中找到两个节点的最近公共祖先】

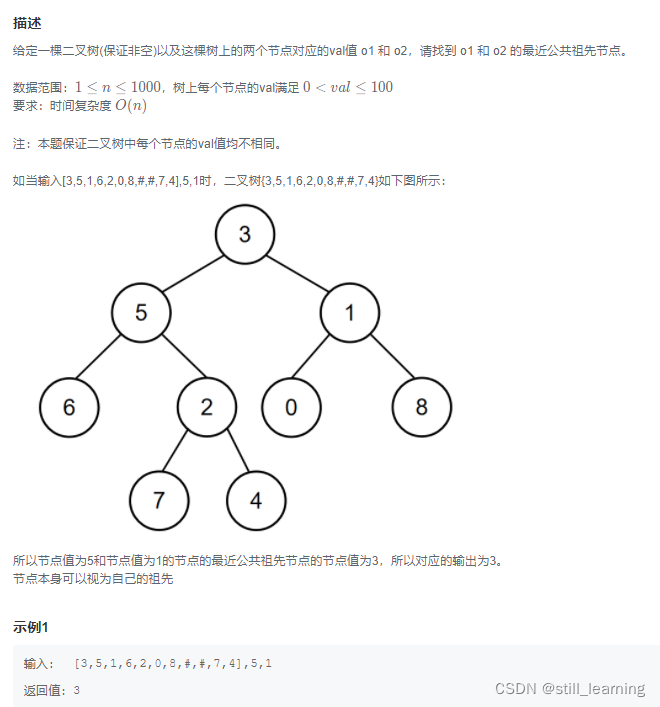
一开始因为漏掉一些关键信息吃了大亏，大家要注意有两点：

1. 保证二叉树的每个节点的val值不同（这意味着只有一种答案，不需要计算多个距离，找最短的那个）
2. 结点本身视为自己的祖先（这就是说1->2，1和2共同祖先是1）

v1 – 搜索存表

基本思路是这样的，遍历这棵树，找到要寻找的两个结点的位置，并且把他们的所有父节点存下来。
遍历完成后，比较两个父节点数组，找到最后一个相同的结点，就是最近公共祖先。

oo1,oo2 = None, None
csq, sq1, sq2 = [], None, None
import copy
def search(root):
    global csq, sq1,sq2,oo1,oo2
    if not root:
        return None
    csq.append(root.val)
    if root.val == oo1:
        sq1 = csq.copy()
    if root.val == oo2:
        sq2 = csq.copy()
    if sq1 and sq2:
        return None
    search(root.left)
    search(root.right)
    csq.pop()
    return None
class Solution:
    def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
        # write code here
        global oo1,oo2
        oo1 = o1
        oo2 = o2
        search(root)
#         print(sq1)
        mlen = min(sq1.__len__(), sq2.__len__())
        for i in range(mlen):
            if i==mlen-1 and sq1[i] == sq2[i]:
                return sq1[i]
            if sq1[i] != sq2[i]:
                return sq1[i-1]
        return sq1[0]

v2 –

参考网上一些大神的写法，递归可以直接做，因为最近的结点满足这样一个条件：
要找的结点同时存在在左右子树中；或者当前结点就是要找的结点，并且要找到另一个结点在其左右子树中。此时我们就返回这个结点的值，一直往回传就好了。

class Solution:
    def lowestCommonAncestor(self , root: TreeNode, o1: int, o2: int) -> int:
        def dfs(root, o1, o2):
            if not root:
                return None 
            left = dfs(root.left, o1, o2)
            right = dfs(root.right, o1, o2)
            if right == -1 and left == -1:       #如果左右都找到，返回这个root的值
                return root.val

            if root.val == o1 or root.val == o2: #如果当前结点是要找的结点
                if left == -1 or right == -1:      #并且左右子树中找到了，那么这个点就是最邻近的结点
                    return root.val
                return -1                        #返回找到
            # 剩下一种情况就是只找到一种
            return left if left else right       #如果左边找到了就返回左边，右边找到了就返回右边
        res = dfs(root, o1, o2)
        return res