[数据结构与算法] C++ 实现红黑树结构

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> C++ 实现红黑树结构 -> 正文阅读

[数据结构与算法]C++ 实现红黑树结构

前言

本文将与读者一同使用C++语言完成红黑树的编写。阅读前，希望你已经掌握了红黑树的基本原理，并对各种操作有印象。如果你不确定自己的知识储备是否足以继续阅读，欢迎阅读《红黑树详解》文章：

后文将针对代码设计与实现展开研究，不再对红黑树的性质与原理等进行过多的赘述。

直接查看源码

如果你不想跟着本文一起学习，而是想直接看代码，请到这里：

RedBlackTree - Github

设计

希望的效果

我们希望按照面向对象的思路，将红黑树封装到类内。从外部看，并不知道它内部是一个红黑树结构，只知道它具有键到数据的映射能力（注意，《红黑树详解》因专注探讨红黑树本身的性质，只考虑了键，忽略了数据。实际编写时不能这样简化）。
即：我们希望我们的红黑树类对外具有以下性质：

键的数据类型任意。
数据的数据类型任意。
拥有“设置”能力。
拥有“查找”能力。
拥有“删除”能力。

例如，我们希望设计一个从字符串到整数的映射，那么我们在创建对象的时候，希望能像下面这样创建：

RedBlackTree<std::string, int> obj;

之后，我们希望能对对象实现以下操作：

// 设置三个从string到int的映射。
obj.setData("沈", 1);
obj.setData("陈", 2);
obj.setData("彭", 3);

int a = obj.getData("陈"); // 将“陈”对应的整数赋值给a. 此时，a应该等于2.

obj.setData("彭", 5); // 对已有数据，应该进行更新操作。

a = obj.getData("彭"); // 此时，a应该等于5. 
a = obj.getData("李"); // 由于“李”这个键未设置，这句话应该导致运行错误。

obj.removeKey("彭"); // 将“彭”从对象中移除。
a = obj.getData("彭"); // 因为“彭”已经不在对象里了，这句话应该导致运行错误。

如上，这个类对外表现的能力刚好对应了红黑树的插入、查找、删除操作。但在调用者看来，他并不知道你的类内部是什么结构，他只是发现你做的这个类能够实现一定的映射功能，并且很好用。
接下来，我们将一起完成这个红黑树类的编写，并一同完成单元测试。

节点结构

因为红黑树是由节点组成的，我们先把节点定义好。
由于节点有两种颜色，我们补充定义一个枚举类来表示颜色：

enum class NodeColor {
    RED, BLACK
};

节点本身应该存储以下信息：

节点键值
节点数据
节点颜色
父节点指针
左孩子指针
右孩子指针

因为我们希望节点键值和数据都是任意的，我们需要引入一个模板（注意，所谓“任意”，指的是我们可以用这个类创建适用于不同数据类型的对象。对于已经创建出来的对象，它的键和数据的类型不能变）。

template <
    typename KeyType, // 键的数据类型
    typename DataType // 数据的数据类型
>

如此，节点的结构体可以这样定义：

struct Node {
	KeyType key;
	DataType data;
	NodeColor color;
	Node* father;
	Node* leftChild;
	Node* rightChild;
};

红黑树类

红黑树由节点组成，节点之间构成树形图。
如节点的定义一样，我们希望这个类适用于不同数据类型，因此要借助函数模板。

template <typename KeyType, typename DataType>
class RedBlackTree {}

只要知道根节点，就能遍历整棵树。
我们为红黑树类添加一个私有成员，用于存储根节点：

private:
    Node* root = nullptr; // 初始为空。

前面的分析已经提到，我们的红黑树需要对外展现出查找、插入、删除的能力。因此，我们设计三个函数：

public:
    /** 获取数据。 */
    DataType& getData(const KeyType& key);
    /** 设置数据。 */
    RedBlackTree<KeyType, DataType>& setData(const KeyType& key, const DataType& data);
    /** 删除键。 */
    RedBlackTree<KeyType, DataType>& removeKey(const KeyType& key);

为方便对象的使用，我们加入“清空”能力和“查询键是否存在”能力：

public:
    /** 查询键是否存在。 */
    bool hasKey(const KeyType& queryKey);
    /** 清空。 */
    void clear();

你一定注意到，setData()和removeKey()的返回类型是一个红黑树对象的引用。对此，可能产生两个问题。

Q：为什么要这么设计？

A：我们将这两个函数的返回设为对象自身，以此提供连续操作的功能。如下：

RedBlackTree<std::string, int> obj;
obj.setData("a", 97)
   .setData("c", 99)
   .setData("d", 100)
   .setData("f", 102);

obj.removeKey("c")
   .removeKey("d");

Q：对于removeKey(...)函数，如何告知调用者是否删除成功？

A：我们选择在无法找到删除目标时抛出异常，以此告知调用者。因此，调用者可以这样编写代码：

try {
    obj.removeKey("x");
    std::cout << "删除成功！" << std::endl;
} 
catch (std::runtime_error& e) {
    std::cout << "删除失败！" << std::endl;
    std::cout << "原因：" << e.what() << std::endl;
}

当然，我们需要设计构造函数和析构函数。为方便操作，我们再加入以下内部函数：

释放内存
左旋
右旋
修复“连续红色节点”问题
修复“节点失衡问题”

public:
    RedBlackTree();
    ~RedBlackTree();
private:
    void cleanup(Node* node);
    void rotateLeft(Node* node);
    void rotateRight(Node* node);
    /**
	 * 修复“连续红色节点”问题。当出现当前节点和父节点同为红色时，需要进行修复。
	 * @param node “连续红色节点”中的子节点。
	 */
    void fixContinuousRedNodeProblem(Node* node);
    /**
	 * 修复“左右孩子不平衡”问题。当某边删除黑色节点后，可能产生此问题。
	 * @param node 失衡问题所在的较轻的节点。
	 */
    void fixUnbalancedChildrenProblem(Node* node);

接下来，我们将上面的功能一一实现即可。

功能实现

内存释放函数（cleanup）

回忆函数定义的样子：

void cleanup(Node* node);

过程与二叉树的内存释放方式没有区别。很简单。

if (node->leftChild != nullptr) {
    cleanup(node->leftChild);
}
if (node->rightChild != nullptr) {
    cleanup(node->rightChild);
}
delete node;

注意，我们没有对传入节点 node 做非空判断。由于这是内部函数，我们保证自己在调用这个函数时先对传入节点做非空判断即可。
事实上，我们只会往这个函数传入根节点。

析构函数和清空（clear）函数

函数定义如下：

~RedBlackTree();
void clear();

因为我们已经写好了内存释放函数，直接调用它就行。但别忘了对根节点做非空检查。

if (this->root != nullptr) {
    this->cleanup(this->root);
    this->root = nullptr;
}

左旋

函数定义如下：

void rotateLeft(Node* node);

在草稿纸上画好左旋操作涉及的所有节点，旋转前后的图形，想清楚涉及哪些指针的改变，然后即可编写代码。

Node* father = node->father;
Node* targetRoot = node->rightChild;

// 重新绑定子树的根。
if (father == nullptr) {
    this->root = targetRoot;
}
else {
    if (node == father->leftChild) {
        father->leftChild = targetRoot;
    }
    else {
        father->rightChild = targetRoot;
    }
}
targetRoot->father = father;

node->rightChild = targetRoot->leftChild; // 孩子有可能是 nullptr
if (node->rightChild != nullptr) { // 只有当孩子不是空的时候，才可尝试重新绑定父节点。
    node->rightChild->father = node;
}
targetRoot->leftChild = node;
node->father = targetRoot;

右旋

此部分与左旋高度相似，希望读者自行完成。也可通过文末链接直接查看完整源代码。

获取数据（getData）

定义如下：

DataType& getData(const KeyType& key);

我们先按照二叉查找树的方式尝试查找节点。如果找到了，就把节点的数据返回。否则，抛出异常。

Node* currentNode = root;
while (currentNode != nullptr) {
    if (key == currentNode->key) {
        return currentNode->data; // 找到对应键。
    }
    else if (key < currentNode->key) {
        currentNode = currentNode->leftChild; // 目标键小于当前键，向左查找。
    }
    else { // key > currentNode->key
        currentNode = currentNode->rightChild; // 目标键大于当前键，向右查找。
    }
}

throw std::runtime_error("could not find your key in the object."); // 找不到对应键。抛出异常。

判断键是否存在（hasKey）

如果你看懂了获取数据（getData）的过程，判断存在（hasKey）对你来说应该非常简单。希望你能自行完成。

插入数据（setData）

函数定义：

RedBlackTree<KeyType, DataType>& setData(const KeyType& key, const DataType& data);

当我们找不到键时，要创建新节点，并检查新节点的加入是否破坏了红黑树的性质。
如果节点正在树上，更新值即可，不用做其他操作。

首先，我们要寻找键，并处理键已在树上的情况。这种情况十分简单。

Node* currentNode = root;
Node* currentFather = nullptr;

while (currentNode != nullptr) {
    if (key == currentNode->key) { // 找到对应键。
        currentNode->data = data;
        return *this; // 更新完成。结束。
    }
    else {
        currentFather = currentNode;
        currentNode = (key < currentNode->key ? currentNode->leftChild : currentNode->rightChild);
    }
}

// 如果是更新现有键值，则在上面的循环里会触发 return.

之后，我们创建新节点，并尝试插入。注意，如果查找后的父节点也是空的，说明要插入的节点是红黑树的第一个节点，也就是根节点。此时，这个节点应该设为黑色。

// 下面部分负责创建新的节点，完成新数据的存储。

/*
    此时，currentNode 指向 nullptr, currentFather 指向最后遍历到的节点，也可能是 nullptr.
    插入时，新节点设为红色，根据键值插入到最后一个节点的左或右。
*/

// 创建新节点。
currentNode = new Node;
currentNode->father = currentFather;
currentNode->leftChild = nullptr;
currentNode->rightChild = nullptr;
currentNode->key = key;
currentNode->data = data;

// 如果树是空的，插入节点设为根即可。
if (currentFather == nullptr) {
    currentNode->color = NodeColor::BLACK;
    this->root = currentNode;
    return *this;
}

否则，我们要将节点设为红色，然后尝试进行“连续红色节点问题”的修复。
注意，我们有两种处理逻辑可以选择。

先检测是否存在问题，在存在问题时再调用函数。这时，我们认为“修复”函数的功能是修正已有问题。
我们可以直接调用“修复”函数，将检测过程写到“修复”函数内。这样，“修复”函数同时具备了检测和检测后修正的能力。

为让代码显得更加优雅，我们选择后者。

// 下面处理树是非空时的情况。
// 先将节点设为红色。
currentNode->color = NodeColor::RED;
// 将新节点绑定到父节点。
if (key < currentFather->key) {
    currentFather->leftChild = currentNode;
}
else {
    currentFather->rightChild = currentNode;
}

// 对可能出现的“连续红色节点”问题进行修复。
this->fixContinuousRedNodeProblem(currentNode);
return *this;

删除键

这是整个红黑树最难的部分。我们还是先回顾函数定义：

RedBlackTree<KeyType, DataType>& removeKey(const KeyType& key);

首先，我们需要查找删除的键是不是在树上。如果不是，就抛出异常。

Node* currentNode = root;

while (currentNode != nullptr) {
    if (key == currentNode->key) {
        break; // 键匹配，查询成功。
    }
    else {
        currentNode = (key < currentNode->key ? currentNode->leftChild : currentNode->rightChild);
    }
}

if (currentNode == nullptr) {
    throw std::runtime_error("could not find your key in the object."); // 找不到对应键。抛出异常。
}

如果函数没有抛出异常，说明已经找到了要删除的节点。我们采用替代法，将要删除的目标移动到叶子部位。
特别注意，移动过程中，我们需要分多种情况分别处理。

该节点有一个孩子还是两个孩子？
该节点的替代者，是不是该节点的孩子？

对于第一个问题，如果节点有两个孩子，或者只有右孩子，寻找后继节点替代。否则，寻找前驱节点替代。
对于第二个问题，如果替代节点的父亲不是原节点，则删除时涉及替代节点的父亲及原节点的所有孩子的变动。但是，当替代节点正是原节点的亲孩子时，直接交换指针可能会导致出现自环。

如图所示（黄色表示原节点，红色表示替代节点）：

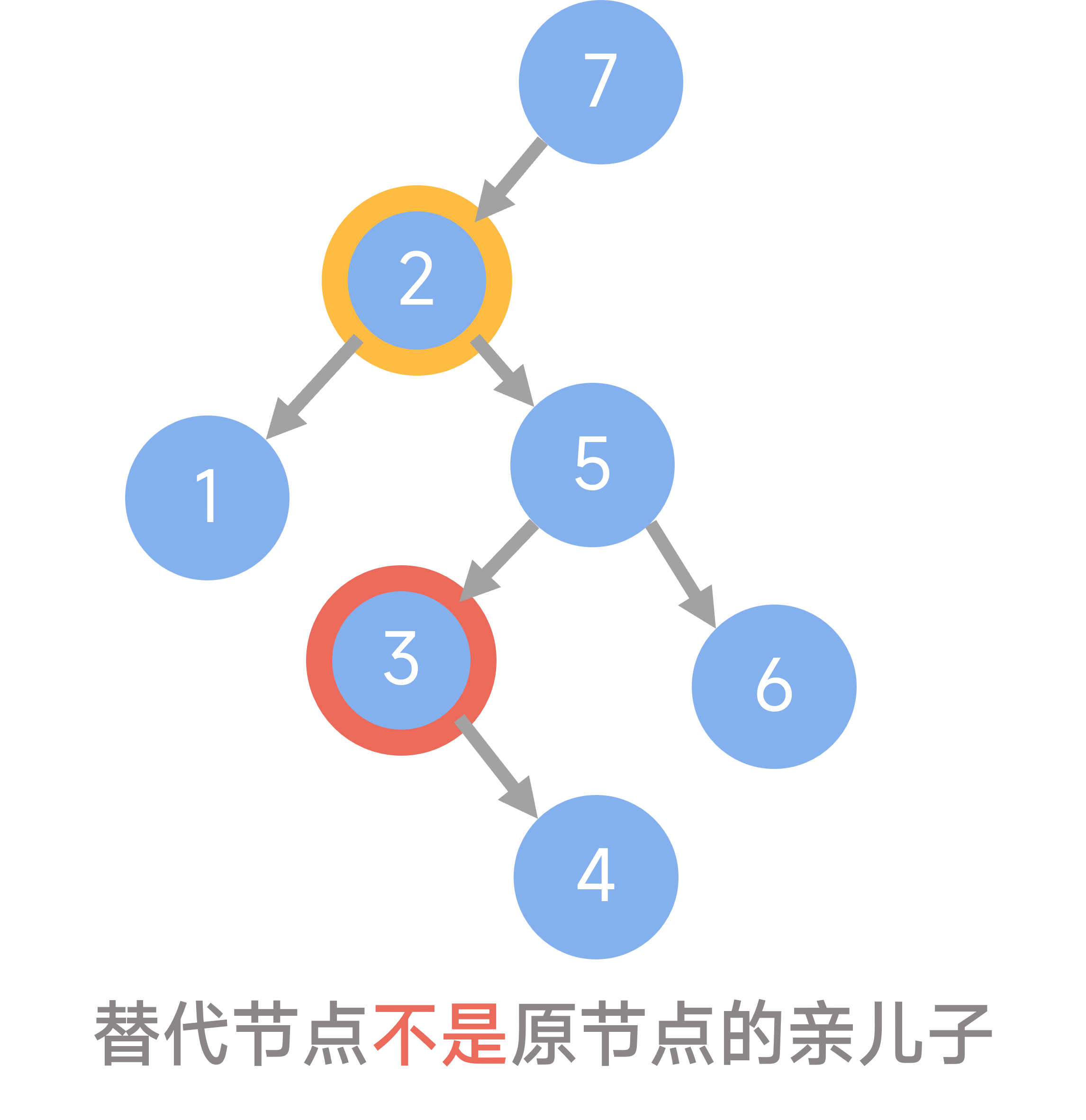
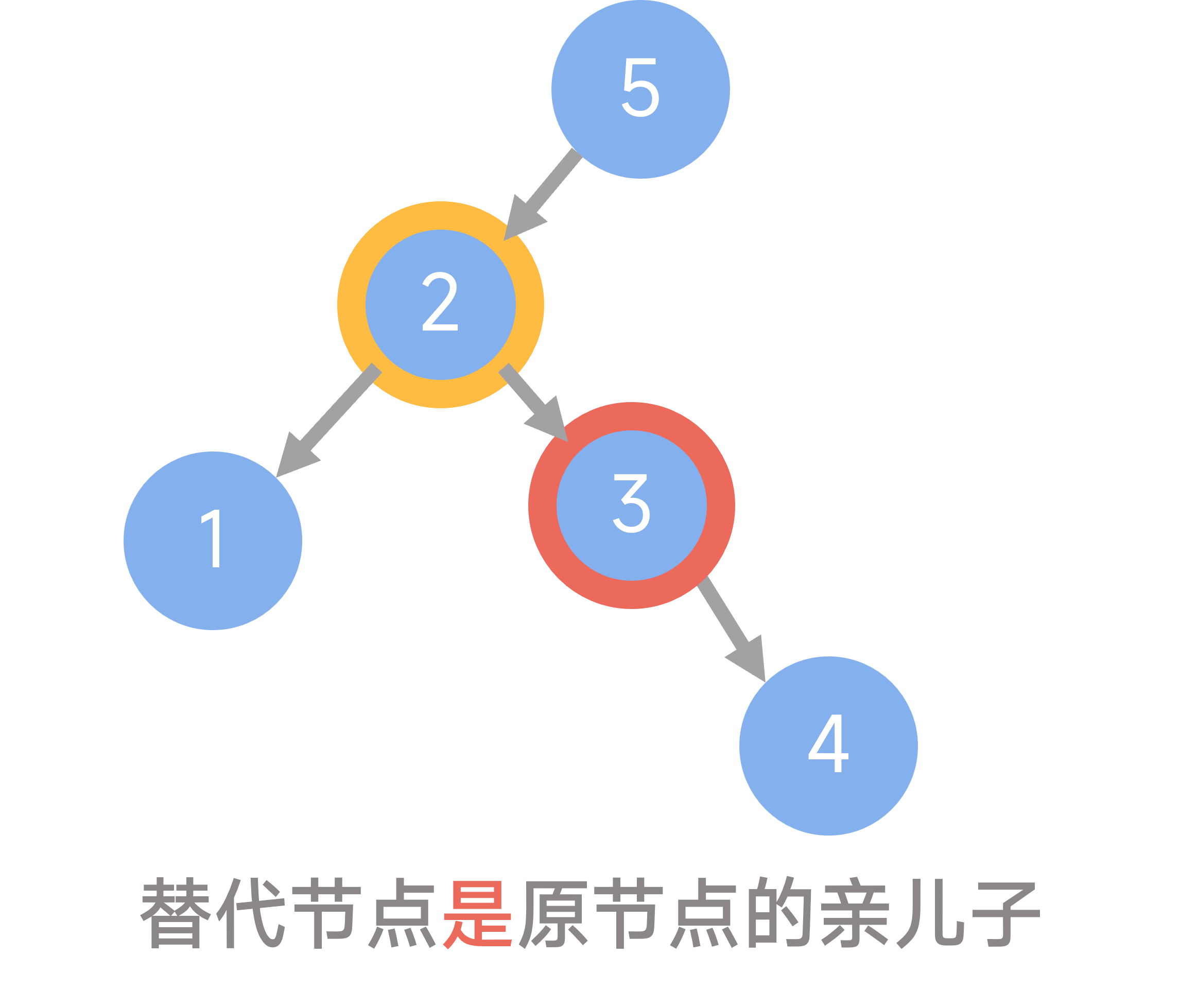
在这里插入图片描述

此外，在修改其他节点信息的时候，对于可以为空的节点，必须先做非空检查。

// 只要有至少一个孩子，就要继续寻找替代节点。
while (currentNode->leftChild != nullptr || currentNode->rightChild != nullptr) {
    if (currentNode->rightChild != nullptr) {
        // 当前节点有右孩子。
        // 使用后继节点代替原删除节点。
        // 注意：后继节点的左孩子一定是 nullptr.
        Node* replacementNode = currentNode->rightChild;
        while (replacementNode->leftChild != nullptr) {
            replacementNode = replacementNode->leftChild;
        }

        struct {
            Node* leftChild;
            Node* rightChild;
            NodeColor color;
            Node* father;
        } currentNodeInfo = {
                currentNode->leftChild, currentNode->rightChild,
                currentNode->color, currentNode->father
        }, replacementNodeInfo = {
                replacementNode->leftChild, replacementNode->rightChild,
                replacementNode->color, replacementNode->father
        };

        // 交换颜色。
        currentNode->color = replacementNodeInfo.color;
        replacementNode->color = currentNodeInfo.color;

        // 编辑父节点。
        if (currentNodeInfo.father != nullptr) {
            if (currentNodeInfo.father->leftChild == currentNode) {
                currentNodeInfo.father->leftChild = replacementNode;
            }
            else {
                currentNodeInfo.father->rightChild = replacementNode;
            }
        }
        else {
            this->root = replacementNode;
        }

        // 编辑 currentNode 左孩子的信息。
        if (currentNodeInfo.leftChild != nullptr) {
            currentNodeInfo.leftChild->father = replacementNode;
        }

        // 编辑 replacementNode 右孩子的信息（如果有）。
        if (replacementNodeInfo.rightChild != nullptr) {
            replacementNodeInfo.rightChild->father = currentNode;
        }
        
        currentNode->leftChild = nullptr; // 替换节点的左孩子一定是 nullptr.
        currentNode->rightChild = replacementNodeInfo.rightChild;
        if (replacementNodeInfo.father == currentNode) {
            currentNode->father = replacementNode;
        }
        else {
            currentNode->father = replacementNodeInfo.father;
        }

        replacementNode->leftChild = currentNodeInfo.leftChild;
        replacementNode->father = currentNodeInfo.father;
        if (currentNodeInfo.rightChild == replacementNode) {
            replacementNode->rightChild = currentNode;
        }
        else {
            replacementNode->rightChild = currentNodeInfo.rightChild;
        }

        if (currentNodeInfo.rightChild != replacementNode) {
            currentNodeInfo.rightChild->father = replacementNode;
            replacementNodeInfo.father->leftChild = currentNode;
        }
    } // if (当前节点有右孩子)
    else { // 当前节点有左孩子，但没有右孩子。
        // 使用前驱节点代替原删除节点。
        // 注意：前驱节点的右孩子一定是 nullptr.
        Node* replacementNode = currentNode->leftChild;
        while (replacementNode->rightChild != nullptr) {
            replacementNode = replacementNode->rightChild;
        }

        struct {
            Node* leftChild;
            Node* rightChild;
            NodeColor color;
            Node* father;
        } currentNodeInfo = {
                currentNode->leftChild, currentNode->rightChild,
                currentNode->color, currentNode->father
        }, replacementNodeInfo = {
                replacementNode->leftChild, replacementNode->rightChild,
                replacementNode->color, replacementNode->father
        };

        // 交换颜色。
        currentNode->color = replacementNodeInfo.color;
        replacementNode->color = currentNodeInfo.color;

        // 编辑父节点。
        if (currentNodeInfo.father != nullptr) {
            if (currentNodeInfo.father->leftChild == currentNode) {
                currentNodeInfo.father->leftChild = replacementNode;
            }
            else {
                currentNodeInfo.father->rightChild = replacementNode;
            }
        }
        else {
            this->root = replacementNode;
        }

        // 编辑 currentNode 右孩子的信息。
        if (currentNodeInfo.rightChild != nullptr) {
            currentNodeInfo.rightChild->father = replacementNode;
        }

        // 编辑 replacementNode 左孩子的信息（如果有）。
        if (replacementNodeInfo.leftChild != nullptr) {
            replacementNodeInfo.leftChild->father = currentNode;
        }

        currentNode->rightChild = nullptr; // 替换节点的右孩子一定是 nullptr.
        currentNode->leftChild = replacementNodeInfo.leftChild;
        if (replacementNodeInfo.father == currentNode) {
            currentNode->father = replacementNode;
        }
        else {
            currentNode->father = replacementNodeInfo.father;
        }

        replacementNode->rightChild = currentNodeInfo.rightChild;
        replacementNode->father = currentNodeInfo.father;
        if (currentNodeInfo.leftChild == replacementNode) {
            replacementNode->leftChild = currentNode;
        }
        else {
            replacementNode->leftChild = currentNodeInfo.leftChild;
        }

        if (currentNodeInfo.leftChild != replacementNode) {
            currentNodeInfo.leftChild->father = replacementNode;
            replacementNodeInfo.father->rightChild = currentNode;
        }
    } // 当前节点有左孩子，但没有右孩子。
} // while (currentNode->leftChild != nullptr || currentNode->rightChild != nullptr)

// 至此，删除目标没有子树。

如果删除目标是根，我们需要在删除节点的同时，将红黑树对象的根设为空。
如果删除目标是红色节点，则在删除并取消其父节点对它的绑定后，不用做其他操作。
如果删除目标是黑色节点，需要做分类处理。

if (currentNode == this->root) { // 删除的是根。
    this->root = nullptr;
    delete currentNode;
} // 删除的是根。
else if (currentNode->color == NodeColor::RED) 
{
    if (currentNode == currentNode->father->leftChild) 
    {
        currentNode->father->leftChild = nullptr;
    }
    else {
        currentNode->father->rightChild = nullptr;
    }
    delete currentNode;
} // 要删除的是红色的叶节点。
else { // 要删除的是黑色的叶节点。
    ...
}

如果你仔细阅读了前面的所有代码，会发现，我们一直要对“左”和“右”做分别的处理。为方便这个过程，我们补充定义一个枚举类：

enum class ChildSide {
    LEFT, RIGHT
};

之后，寻找兄弟节点，然后按照之前分析过的进行分类处理即可。

// 目标节点的父节点一定存在。因为目标节点是黑色的，所以兄弟一定存在。
Node* sibling = (currentNode->father->leftChild != currentNode ?
    currentNode->father->leftChild : currentNode->father->rightChild);

Node* currentFather = currentNode->father;

ChildSide siblingSideToFather = 
    (sibling == currentFather->leftChild ? ChildSide::LEFT : ChildSide::RIGHT);

// 前面已经找完了与删除目标相关的节点。现在可以删掉目标节点了。
// 取消父节点对它的绑定。
if (currentFather->leftChild == currentNode) {
    currentFather->leftChild = nullptr;
}
else {
    currentFather->rightChild = nullptr;
}
// 释放节点。
delete currentNode;

// 接下来开始分情况讨论。

之后，对不同情况分别做处理。情况非常多，在此先展示分类方式：

if (currentFather->color == NodeColor::RED) {
    // 父节点是红色时，兄弟节点一定是黑色的。
    if (sibling->leftChild != nullptr && sibling->rightChild != nullptr) {...}
    else if (siblingSideToFather == ChildSide::RIGHT && sibling->leftChild != nullptr) {...}
    else if (siblingSideToFather == ChildSide::LEFT && sibling->rightChild != nullptr) {...}
    else if (siblingSideToFather == ChildSide::RIGHT && sibling->rightChild != nullptr) {...}
    else if (siblingSideToFather == ChildSide::LEFT && sibling->leftChild != nullptr) {...}
    else { // sibling 没有孩子。
        ...
    }

} // currentFather->color == NodeColor::RED
else { // currentFather->color == NodeColor::BLACK
    if (sibling->color == NodeColor::BLACK
        && sibling->leftChild != nullptr && sibling->rightChild != nullptr)
    {
        // 兄弟是黑色的，且兄弟有两个孩子。那么这两个孩子一定是红色的。
        if (siblingSideToFather == ChildSide::RIGHT) {...}
        else {...}
    } // 兄弟是黑色，且有两个孩子。
    else if (sibling->color == NodeColor::BLACK &&
        (sibling->leftChild != nullptr || sibling->rightChild != nullptr))
    {
        // 兄弟是黑色，且有一个孩子（一定是红色）。
        if (siblingSideToFather == ChildSide::RIGHT && sibling->rightChild != nullptr) {...}
        else if (siblingSideToFather == ChildSide::RIGHT && sibling->leftChild != nullptr) {...}
        else if (siblingSideToFather == ChildSide::LEFT && sibling->leftChild != nullptr) {...}
        else {...}
    } // 兄弟是黑色，且有一个孩子。
    else if (sibling->color == NodeColor::BLACK) {
        if (currentFather->leftChild == nullptr) {...}
        else {...}
    } // 兄弟是黑色的，且没有孩子。
    else {
        // 兄弟是红色的。那么兄弟一定有两个黑色的孩子。
        sibling->color = NodeColor::BLACK;
        currentFather->color = NodeColor::RED;
        if (siblingSideToFather == ChildSide::RIGHT) {
            ...
            if (currentFather->rightChild != nullptr) {...}
        }
        else {
            ...
            if (currentFather->leftChild != nullptr) {...}
        }
    }
}

篇幅有限，无法将所有情况的修复代码一一呈现。现挑选两个具有代表性的情况进行讲解。

父节点是红色，并且兄弟有两个孩子时：

// 父节点是红色时，兄弟节点一定是黑色的。
if (sibling->leftChild != nullptr && sibling->rightChild != nullptr)
{
    /*
        X: 被删除; R: Red; B: Black
          R
         / \
        X   B
           / \
          R   R   或其对称形态。
    */
    // 兄弟的左右孩子都是红色。
    // 注意：如果这个黑色的叔叔有孩子，那么孩子一定是红色的。
    // 操作：对兄弟做旋转，再对父节点做旋转。父节点设为黑色，兄弟设为红色。
    sibling->color = NodeColor::RED;
    currentFather->color = NodeColor::BLACK;

    if (siblingSideToFather == ChildSide::RIGHT) {
        sibling->rightChild->color = NodeColor::BLACK;
        this->rotateLeft(currentFather);
    }
    else {
        sibling->leftChild->color = NodeColor::BLACK;
        this->rotateRight(currentFather);
    }
}

父节点是黑色，兄弟是黑色，但是兄弟没有孩子时：

// 兄弟是黑色，但是没有孩子。
/*
      B          B
     / \   ->   / \
    X   B      X   R
*/
if (currentFather->leftChild == nullptr) {
    currentFather->rightChild->color = NodeColor::RED;
    this->fixUnbalancedChildrenProblem(currentFather);
}
else {
    currentFather->leftChild->color = NodeColor::RED;
    this->fixUnbalancedChildrenProblem(currentFather);
}

修复“连续红色问题”

函数定义：

void fixContinuousRedNodeProblem(Node* node);

当一次修复后，局部根节点和其父节点同为红色时，该函数会被递归调用。对此，我们不能真的让它递归运行，不然可能出现栈溢出问题。
由于这个“递归”过程很简单，我们完全可以转换为循环运行。
循环中，要注意对红黑树树根的特殊处理。因为它是没有父亲的，同时也是“递归”出口。

Node* currentNode = node;

// 只有当当前节点是红色时，才可能在父节点为红色时违背红黑树规则，于是要进行修复操作。
while (currentNode->color == NodeColor::RED) {
    Node* currentFather = currentNode->father;
    if (currentFather == nullptr) {
        // currentNode 是根节点。
        currentNode->color = NodeColor::BLACK;
        break;
    }
    else if (currentFather->color == NodeColor::BLACK) {
        // 父节点是黑色，不存在“连续红色节点”问题。
        break;
    }

    // 如果执行到了这里，说明父节点和目标节点都是红色的。

    // 如果父节点是红色的，那么它（父节点）一定不是根，所以祖父存在。
    Node* currentGrandpa = currentFather->father;

    // 寻找叔节点（可能为空）。
    Node* uncle =
        (currentGrandpa->leftChild != currentFather ?
            currentGrandpa->leftChild : currentGrandpa->rightChild);

    if (uncle != nullptr && uncle->color == NodeColor::RED) {
        // 叔叔存在并且是红色，进行反色操作。

        uncle->color = NodeColor::BLACK;
        currentFather->color = NodeColor::BLACK;
        currentGrandpa->color = NodeColor::RED;

        // 将当前节点设为爷爷节点。
        currentNode = currentGrandpa;
    }
    else {
        // 叔叔为黑色或不存在，进行旋转操作。
        // 旋转的每一种情况都可以保证树满足红黑树的要求。所以，进入本分支后将跳出修复函数。

        // 如果父节点是祖父的左孩子...
        if (currentFather == currentGrandpa->leftChild) {
            if (currentNode == currentFather->leftChild) {
                this->rotateRight(currentGrandpa);
                // 重新着色。
                currentFather->color = NodeColor::BLACK;
                currentGrandpa->color = NodeColor::RED;
            }
            else {
                this->rotateLeft(currentFather);
                this->rotateRight(currentGrandpa);
                // 重新着色。
                currentGrandpa->color = NodeColor::RED;
                currentNode->color = NodeColor::BLACK;
            }
        } // if (currentFather == currentGrandpa->leftChild)
        else {
            // 否则，则父节点是祖父的右孩子...

            if (currentNode == currentFather->rightChild) {
                this->rotateLeft(currentGrandpa);
                // 重新着色。
                currentFather->color = NodeColor::BLACK;
                currentGrandpa->color = NodeColor::RED;
            }
            else {
                this->rotateRight(currentFather);
                this->rotateLeft(currentGrandpa);
                // 重新着色。
                currentGrandpa->color = NodeColor::RED;
                currentNode->color = NodeColor::BLACK;
            }
        } // if (currentFather != currentGrandpa->leftChild)

        return;
    }
}

修复“失衡问题”

函数定义：

void fixUnbalancedChildrenProblem(Node* node);

该函数也涉及多种情况的分析讨论，同时也涉及“递归”问题。同样，我们使用循环来规避递归调用函数。
注意，对于修复成功的情况，需要在对应代码块内跳出循环（break）。

Node* currentNode = node;

while (currentNode != this->root) {
    Node* currentFather = currentNode->father;
    Node* sibling = (currentFather->leftChild != currentNode ?
        currentFather->leftChild : currentFather->rightChild);
    ChildSide siblingSideToFather = 
        (sibling == currentFather->leftChild ? ChildSide::LEFT : ChildSide::RIGHT);

    if (currentFather->color == NodeColor::RED) {
        // 父节点为红色。
        // 那么，兄弟一定是黑色的。
        // 此时，兄弟节点的左右孩子一定都存在。
        if (siblingSideToFather == ChildSide::RIGHT
            && sibling->leftChild->color == NodeColor::BLACK) {...}
        else if (siblingSideToFather == ChildSide::LEFT
            && sibling->rightChild->color == NodeColor::BLACK) {...}
        else if (siblingSideToFather == ChildSide::RIGHT
            && sibling->rightChild->color == NodeColor::BLACK)
        {
            ...
        }
        else if (siblingSideToFather == ChildSide::LEFT
            && sibling->leftChild->color == NodeColor::BLACK)
        {
            ...
        }
        else { // 兄弟的左右孩子都是红色的。
            ...
        }
    } // 父节点为红色。
    else { // 父节点为黑色。
        if (sibling->color == NodeColor::RED) { // 兄弟是红色的。
            ...
        } // 兄弟是红色的。
        else { // 兄弟是黑色的。
            if (sibling->leftChild->color == NodeColor::BLACK 
                && sibling->rightChild->color == NodeColor::BLACK) {...}
            else if (siblingSideToFather == ChildSide::RIGHT 
                && sibling->rightChild->color == NodeColor::RED) {...}
            else if (siblingSideToFather == ChildSide::LEFT
                && sibling->leftChild->color == NodeColor::RED) {...}
            else if (siblingSideToFather == ChildSide::RIGHT) {...}
            else {...}
        } // 兄弟是黑色的。
    } // 父节点为黑色。
}

我们选其中一种情况看看：当父节点为黑色、兄弟也是黑色、兄弟的孩子都是黑色时：

/*
      B
     / \
    X   B
       / \
      B   B

    及其对称形态。
*/
sibling->color = NodeColor::RED;
currentNode = currentFather;

单元测试

我们编写简单的单元测试程序来检测红黑树类的运行是否正常。

/**
 * Red Black Tree Module Test
 * by Flower Black
 * 2022.1
 * at Yushan County, Shangrao, Jiangxi
 */

#include <string>

#include "pch.h"
#include "CppUnitTest.h"

#include "../Red Black Tree/RedBlackTree.hpp"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace RedBlackTreeTest
{
	TEST_CLASS(RedBlackTreeTest) 
	{
	public:
		
		TEST_METHOD(OrderedSetGetTest) {
			RedBlackTree<int, int> tree;
			for (int i = 0; i < 20; i++) {
				tree.setData(i, i * i);
			}

			for (int i = 0; i < 20; i++) {
				Assert::AreEqual(i * i, tree.getData(i));
			}
		}

		TEST_METHOD(RandomSetGetTest) {
			int inputList[20] = {
				12, 13, 10, 3, 14, 15, 1, 2, 17, 0, 6, 7, 8, 4, 18, 5, 9, 11, 19, 16
			};

			RedBlackTree<int, int> tree;

			for (int i = 0; i < 20; i++) {
				tree.setData(inputList[i], inputList[i] * inputList[i]);
			}

			for (int i = 0; i < 20; i++) {
				Assert::AreEqual(i * i, tree.getData(i));
			}

			for (int i = 20; i < 30; i++) {
				try {
					tree.getData(i);
					Assert::IsFalse(true); // Junit 风格的 assertFalse.
				}
				catch (...) {
					Assert::IsTrue(true);
				}
			}
		}

		TEST_METHOD(HasKeyFunctionTest) {
			RedBlackTree<int, int> tree;
			for (int i = 0; i < 20; i++) {
				tree.setData(i, i * i);
			}

			for (int i = 0; i < 10; i++) {
				Assert::AreEqual(i * 5 < 20, tree.hasKey(i * 5));
			}
		}

		TEST_METHOD(MissFetchTest) {
			RedBlackTree<int, int> tree;
			for (int i = 0; i < 20; i++) {
				tree.setData(i, i * i);
			}

			for (int i = 0; i < 10; i++) {
				try {
					tree.getData(i * 5);
					Assert::AreEqual(true, i * 5 < 20);
				}
				catch (...) {
					Assert::AreEqual(false, i * 5 < 20);
				}
			}
		}

		TEST_METHOD(RemoveKeyTest) {
			RedBlackTree<int, int> tree;
			for (int i = 0; i < 20; i++) {
				tree.setData(i, i * i);
			}
			for (int i = 0; i < 20; i += 2) {
				tree.removeKey(i);
			}

			for (int i = 0; i < 20; i++) {
				Assert::AreEqual(i % 2 != 0, tree.hasKey(i));
			}
		}

		TEST_METHOD(MixedHashOperationTest) {
			srand((unsigned int)time(0));
			RedBlackTree<std::string, int> tree;
			struct TestObj {
				std::string key;
				int value;
			} testArray[] = {
				{"沈", rand()}, // 0
				{"家的", rand()}, // 1
				{"公子", rand()}, // 2
				{"最最最", rand()}, // 3
				{"帅的", rand()}, // 4
				{"曹安", rand()}, // 5
				{"公路", rand()}, // 6
				{"4800号", rand()}, // 7
				{"四平路1239号", rand()}, // 8
				{"zbhyyds", rand()}, // 9
				{"zyfdltql", rand()}, // 10
				{"larrytj", rand()}, // 11
				{"黄渡", rand()}, // 12
				{"安亭", rand()}, // 13
				{"花桥", rand()}, // 14
				{"昆山", rand()}, // 15
			};

			const int testArraySize = sizeof(testArray) / sizeof(TestObj) / 2 * 2;
			// 上方 (X * 2 / 2) 的作用：保证 testArraySize 是偶数。

			for (int i = 0; i < testArraySize; i += 2) {
				Assert::IsFalse(tree.hasKey(testArray[i].key));
				tree.setData(testArray[i].key, testArray[i].value);
				Assert::IsTrue(tree.hasKey(testArray[i].key));
			}

			for (int i = 0; i < testArraySize; i++) {
				Assert::AreEqual(i % 2 == 0, tree.hasKey(testArray[i].key));
			}

			for (int i = testArraySize - 1; i >= 0; i--) {
				Assert::AreEqual(i % 2 == 0, tree.hasKey(testArray[i].key));
				try {
					int value = tree.getData(testArray[i].key);
					Assert::AreEqual(testArray[i].value, value);
				}
				catch (...) {
					Assert::IsTrue(i % 2 != 0);
				}
			}
			
			// 更新数据测试。
			for (int i = 0; i < testArraySize; i += 2) {
				tree.setData(testArray[i].key, testArray[i + 1].value);
				tree.setData(testArray[i + 1].key, testArray[i + 1].value);
			}

			for (int i = 0; i < testArraySize; i += 2) {
				Assert::IsTrue(tree.hasKey(testArray[i].key));
				Assert::IsTrue(tree.hasKey(testArray[i + 1].key));
				Assert::AreEqual(testArray[i + 1].value, tree.getData(testArray[i].key));
				Assert::AreEqual(testArray[i + 1].value, tree.getData(testArray[i + 1].key));
			}

			// 删除数据测试
			for (int i = 0; i < testArraySize; i += 2) {
				Assert::IsTrue(tree.hasKey(testArray[i].key));
				tree.removeKey(testArray[i].key);
				Assert::IsFalse(tree.hasKey(testArray[i].key));
				for (int j = i + 2; j < testArraySize; j += 2) {
					Assert::AreEqual(testArray[j + 1].value, tree.getData(testArray[j].key));
					Assert::AreEqual(testArray[j + 1].value, tree.getData(testArray[j + 1].key));
				}
			}

			for (int i = 0; i < testArraySize; i++) {
				Assert::AreEqual(i % 2 != 0, tree.hasKey(testArray[i].key));
				try {
					tree.getData(testArray[i].key);
					Assert::IsTrue(i % 2 != 0);
				}
				catch (...) {
					Assert::IsTrue(i % 2 == 0);
				}
			}
		}
	};
}

这个单元测试显然无法完成对整个红黑树结构的测试，但是可以帮助发现一些隐藏的问题。通过测试不代表编写的代码正确，但不通过测试是可以说明代码编写有疏漏的。

后记

到这里，你已经大概了解如何使用C++完成红黑树结构的编写。如果你想阅读完整源码，请到文末链接处查看。
红黑树的一大复杂之处正在于其情况之多。实际编写易用的红黑树结构时，还需要考虑很多其他的问题。
我们在《红黑树详解》中，对红黑树做了很多简化，以此躲避这些外围的问题，这样才能静下心研究红黑树本身。然而在编写代码时，无法逃避这些。虽然每种情况的代码都很简单，但必须分类清晰。但凡有一点错误，查错过程都会是很艰辛的。
希望我的文章对你的学习帮助有启发作用，也感谢你的阅读。