[数据结构与算法]【力扣】101.对称二叉树

题目：

101. 对称二叉树
     给你一个二叉树的根节点 root ， 检查它是否轴对称。
     示例 1：
     

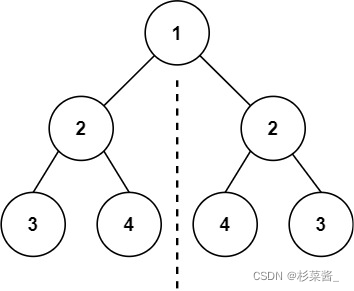
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

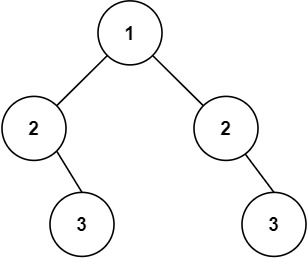
输入：root = [1,2,2,null,3,null,3]
输出：false

方法一：递归

class Solution {
    public boolean isSymmetric(TreeNode root) {
        return check(root,root);
    }
    public boolean check(TreeNode p, TreeNode q){
    	//递归的终止条件是两个节点都为空
			//或者两个节点中有一个为空
			//或者两个节点的值不相等
        if(p == null && q == null){
            return true;
        }
        if(p == null || q == null){
            return false;
        }
        //再递归的比较 左节点的左孩子 和 右节点的右孩子
		//以及比较  左节点的右孩子 和 右节点的左孩子
        return p.val == q.val && check(p.left,q.right) && check(p.right,q.left);
    }
}

复杂度分析 :

假设树上一共 nn 个节点。

• 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)O(n)。
• 空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 nn，故渐进空间复杂度为 O(n)O(n)。

方法二:迭代

思路：

1. 引入一个队列
2. 保证队列中连续的两个节点是相等的

// 方法二：迭代
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null || (root.left == null && root.right == null)){
            return true;
        }
        LinkedList<TreeNode> queue = new LinkedList<>();
        // 将根节点的左右孩子放入队列中
        queue.add(root.left);
        queue.add(root.right);
        while(queue.size() > 0){
        	// 从队列中取两个节点,再比较这两个节点
            TreeNode left = queue.removeFirst();
            TreeNode right = queue.removeFirst();
            // 如果两个节点为空，就进入下一层循环；如果有一个为空，就返回false。
            if(left == null && right == null){
                continue;
            }
            if(left == null || right == null){
                return false;
            }
            if(left.val != right.val){
                return false;
            }
            //让左节点的左孩子、右节点的右孩子入队
            queue.add(left.left);
            queue.add(right.right);
			//让右节点的左孩子、左节点的右孩子入队
            queue.add(right.left);
            queue.add(left.right);
        }
        return true;
    }
}

复杂度分析 :

• 时间复杂度：O(n)O(n)，同「方法一」。
• 空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 nn 个点，故渐进空间复杂度为 O(n)O(n)。