堆排序
一、 堆
堆要满足两个条件:
1.是一个完全二叉树
2.堆中某个节点的值总是不大于或不小于其父节点的值
什么是父节点子节点呢?看下图二叉树:
大顶堆(大根堆):每个父结点的值都大于等于其子节点的值,左边的子节点可以形象称为左孩子,右边的子节点则为右孩子
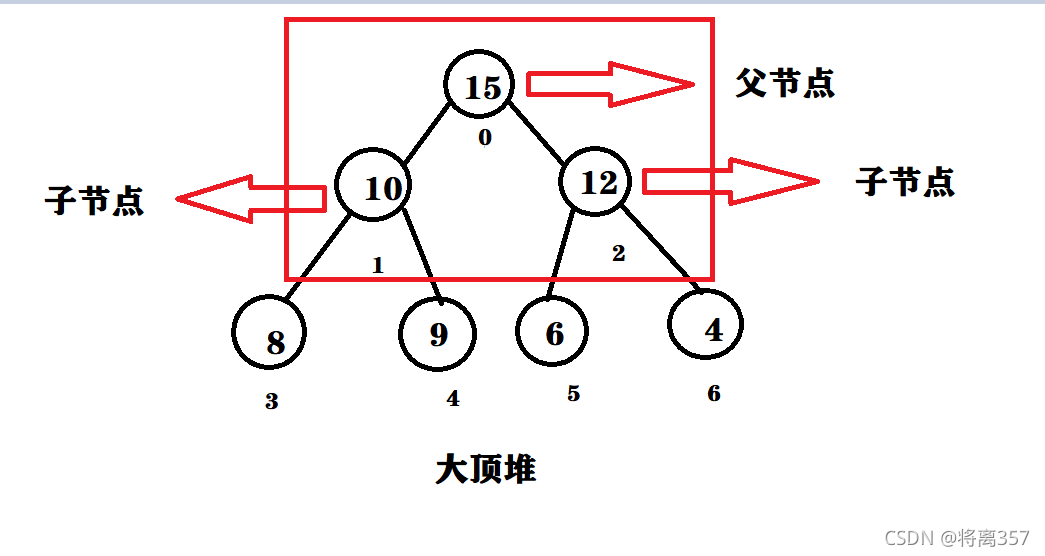
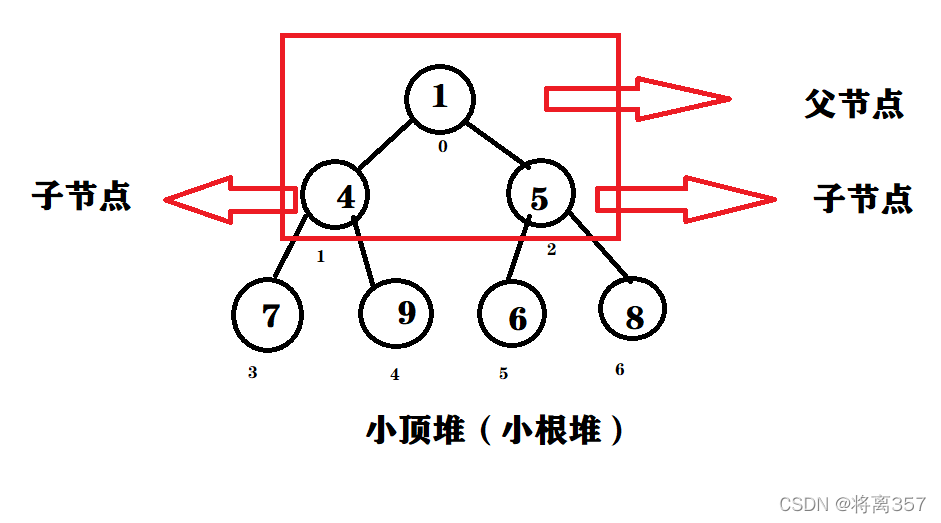
小顶堆(小根堆):每个父结点的值都小于等于其子节点的值
二、基本思想
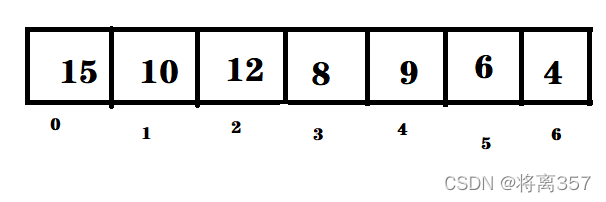
由于堆的连续存储方式,可以采用数组来进行进行存储,将堆中的数字按照一定顺序存入数组中,例如上图中的大顶堆,可以存储如下:
以大顶堆为例,堆排序的基本思路是
1.首先将待排序的数构造为一个大顶堆,那么整个数组的最大值就是堆结构的顶端
2.将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
3.将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,反复这个过程,就可与完成排序
三、代码实现
用 i 表示数组下标,n代表待排序的数字个数,c1、c2为左孩子与右孩子,可以下列公式来寻找第i个节点的父节点与子节点
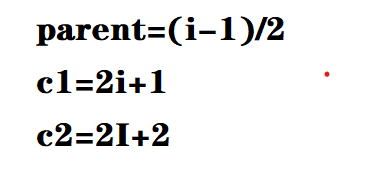
1.heapify:
先将待排序的数字写成树的结构,此时树上的数字并不满足父节点大于或等于其子节点,因此要进行堆化(heapify)
从一个结点出发,将它与左孩子右孩子比较,选择三者中中的最大值作为新的父节点,反复该过程直到成为一个大顶堆
int heapify(int tree[10000],int n,int i)
{
if(i>=n)//i表示数组下标,n代表待排序的数字个数
{
return ;
}
int c1,c2,max;//c1,c2为两个子节点
c1=2*i+1;
c2=2*i+2;
max=i;
if(c1<n&&tree[c1]>tree[max])
{max=c1;}
if(c2<n&&tree[c2]>tree[max])
{max=c2;}
if(max!=i)
{
swap(tree,max,i);//为了方便写一个swap函数,详情见(1)
heapify(tree,n,max);
}
}
(1)swap交换函数
int swap(int arr[10000],int i,int j)
{
int t;
t=arr[i];
arr[i]=arr[j];
arr[j]=t;
}
2.build_heap:从中间的结点开始向上依次堆化
int build_heap(int tree[10000],int n)
{
int last_node=n-1;
int parent=(last_node-1)/2;
int i;
for(i=parent;i>=0;i--)
{
heapify(tree,n,i);
}
}
3.heap_sort:
每将最大值与最后一个节点交换后,堆的结构就被破坏了,需要再次堆化。
我们可以理解为每交换一次最大值,就将连接最大值的树枝砍断,那么需要排列的数就从n变为n-1,继续对n-1个数重复这个过程
int heap_sort(int tree[10000],int n)
{
build_heap(tree,n);
int i;
for(i=n-1;i>=0;i--)
{
swap(tree,i,0);
heapify(tree,i,0);
}
}
完整代码如下:
#include<stdio.h>
int swap(int arr[10000],int i,int j)
{
int t;
t=arr[i];
arr[i]=arr[j];
arr[j]=t;
}
int heapify(int tree[10000],int n,int i)
{
if(i>=n)
{
return ;
}
int c1,c2,max;
c1=2*i+1;
c2=2*i+2;
max=i;
if(c1<n&&tree[c1]>tree[max])
{max=c1;}
if(c2<n&&tree[c2]>tree[max])
{max=c2;}
if(max!=i)
{
swap(tree,max,i);
heapify(tree,n,max);
}
}
int build_heap(int tree[10000],int n)
{
int last_node=n-1;
int parent=(last_node-1)/2;
int i;
for(i=parent;i>=0;i--)
{
heapify(tree,n,i);
}
}
int heap_sort(int tree[10000],int n)
{
build_heap(tree,n);
int i;
for(i=n-1;i>=0;i--)
{
swap(tree,i,0);
heapify(tree,i,0);
}
}
int main()
{
int i,tree[10000],n;
scanf("%d",&n);
scanf("%d",&tree[0]);
for(i=1;i<n;i++)
{
scanf(" %d",&tree[i]);
}
heap_sort(tree,n);
for(i=0;i<n;i++)
{
printf("%d ",tree[i]);
}
return 0;
}
提示:该博客为学习@正月点灯笼《堆排序》的笔记