[Êý¾Ý½á¹¹ÓëËã·¨]Linear Algebra Review

Linear Algebra Review

Matrices and Vectors

Matrix: Rectangular array of numbers

Dimension of matrix: number of rows x number of columns

Refer to matrix of specific dimension: ${\mathbb{R}}^{2¡Á3}$

Refer to specific matrix elements of the matrix: $A_{ij}$("$i,j$ entry" in the $i^{th}$ row, $j^{th}$ column)

Vector: An n$¡Á$ 1 matrix

4-dimensional vector :${\mathbb{R}}^4$

Refer elements in vector: $y_i$=$i^{th} $ element

1-indexed vs 0-indexed

By conventional, use capital letters (such as A,B,C,X ) to refer matrices, and use lower cases (like a,d,c,x,y) to refer to either numbers or just raw numbers or scalars or vectors.

Addition and Scalar

Matrix addition and subtraction

Simply add or subtract each corresponding elements

The dimensions of two matrices to add or subtract must be the same

Scalar multiplication and division

Simply multiply or divide every element by the scalar value

Matrix Vector Multiplication

Details:

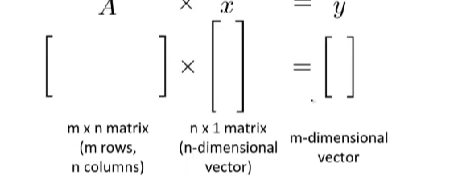
To get $y_i$, multiply $A^{¡ä}s$ $i^{th}$ row with elements of vector $x$, and add them up.

The result is a vector. The number of columns of the matrix must equal the number of rows of the vector.

An m x n matrix multiplied by an n x 1 vector results in an m x 1 vector.

prediction=DataMatrix $?$ parameters

Matrix Matrix Multiplication

Details:

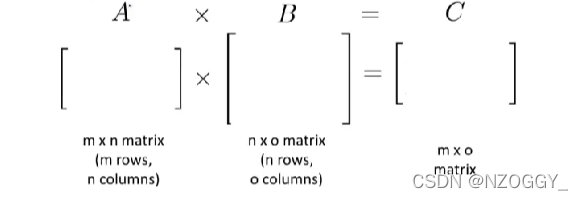
The $i^{th}$ column of the matrix $C$ is obtained by multiplying $A$ with the $i^{th}$ column of $B$.(for $i$ =1,2¡­o)

efficiently make prediction with lots of hypotheses

• To multiply two matrices, the number of columns of the first matrix must equal the number of rows of the second matrix.

Matrix Multiplication

Properties

• not commutative

  Let $A,B$ be matrices, then in general, $A¡ÁBªÁ=B¡ÁA$.(reversing the order of the matrices can change the dimension of outcome)

• enjoy associative property

  $A¡ÁB¡ÁC$

  Let $D=B¡ÁC$. Compute $A¡ÁD$

  Let $E=A¡ÁB$. Compute $E¡ÁC$.

  all give the same answer.

Identity Matrix

Denoted $Ior{I}_{n¡Án}$

• Has 1¡¯s on the diagonal (upper left to lower right diagonal) and 0¡¯s elsewhere.

When multiplied by any matrix of the same dimensions, results in the original matrix.
$$A¡ÁI=I¡ÁA=A$$
(The $I^{¡ä}s$ in the function above have different dimension)

The dimension of $I$ is implicit from the context.

Inverse and Transpose

Matrix Inverse

If $A$ is an m x m matrix (square matrix), and if it has an inverse,
$$A{A}^{?1}=A^{?1}A=I$$
Matrices that don¡¯t have an inverse is singular or degenerate.

Matrix Transpose

Let $A$ be an m x n matrix, and let $B=A^T$. Then $B$ is an n x m matrix, and
$$B_{ij}=A_{ij}$$

Transpose**

Let $A$ be an m x n matrix, and let $B=A^T$. Then $B$ is an n x m matrix, and
$$B_{ij}=A_{ij}$$