🐸青蛙跳台阶

问题描述
一只青蛙🐸一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
问题分析
当n = 1时 有1种方法
直接跳1级
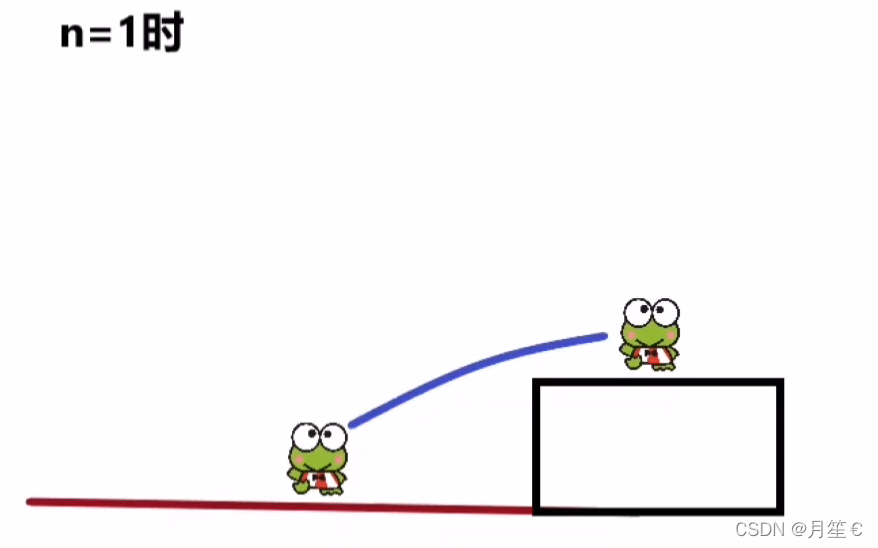
当n = 2时 ,有2种方法
①一次跳1级
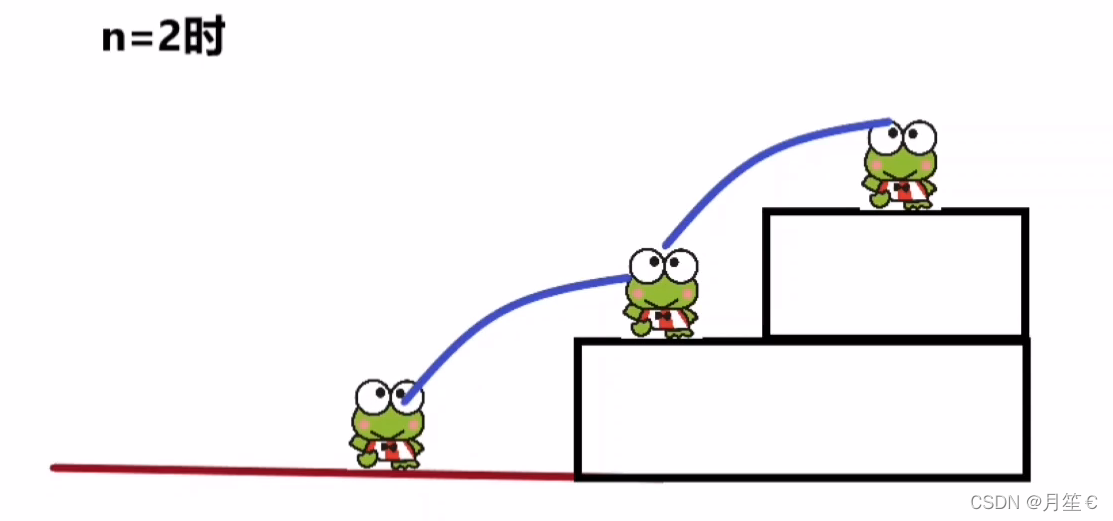
②一次跳2级
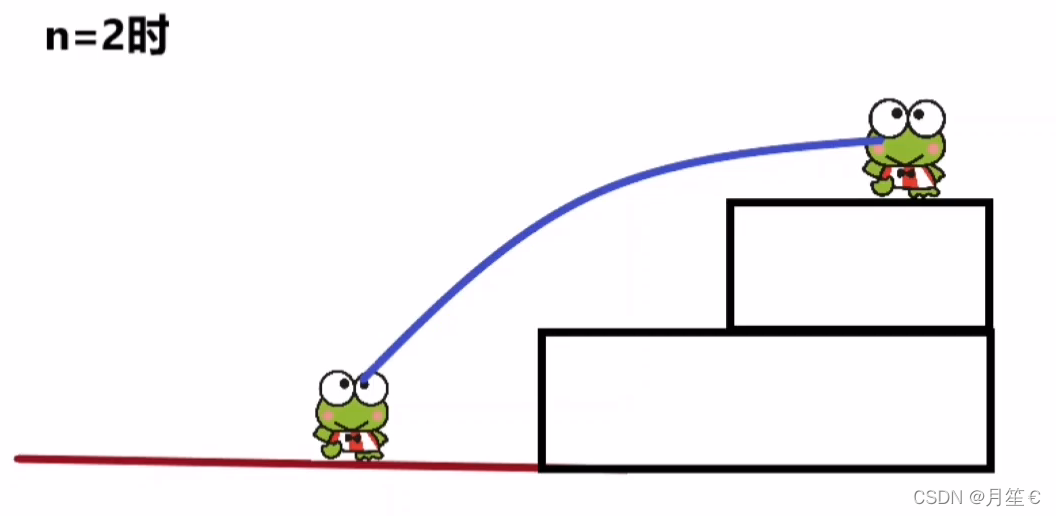
当n = 3时 ,有3种方法。
①一次跳1级
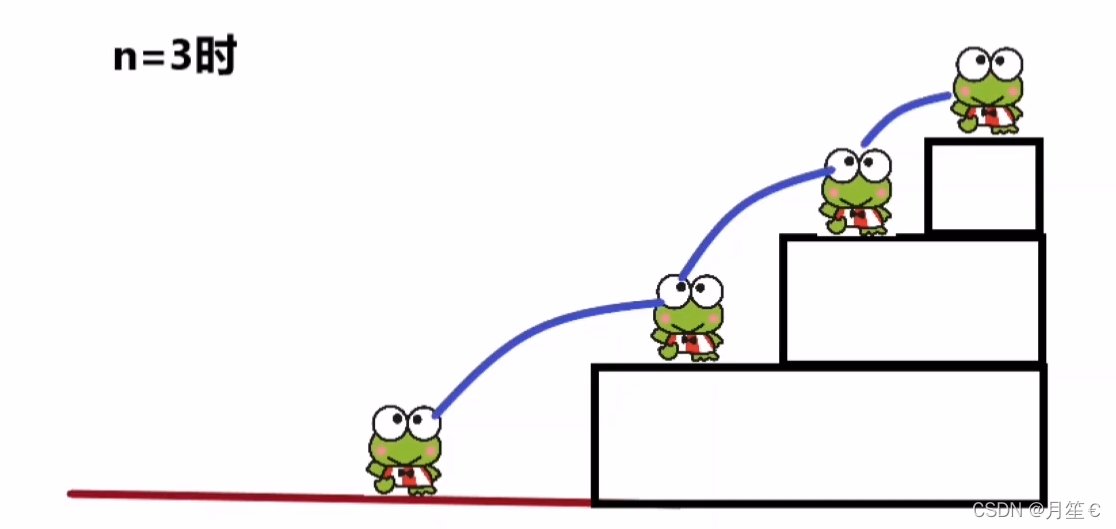
②先跳2级,再跳1级
③先跳1级,再跳2级
很快我们发现当🐸跳n级台阶的时候,最后一次要不跳2级,要不就跳1级,那么跳n级的方法数不就是跳 n - 1级的方法数 ? 跳n - 2级的方法数吗?然后这不就是斐波那契数列吗??
| n | 方法数 |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| … | … |
| n | fib(n - 1) + fib(n - 2) |
代码演示
public class TestDemo {
public static int climbStairs(int n) {
if (n == 0 || n == 1) {
return 1;
}
return climbStairs(n - 1) + climbStairs(n - 2);
}
public static void main(String[] args) {
int res = climbStairs(5);
System.out.println("方法数:" + res);
}
}
运行结果:
算法分析
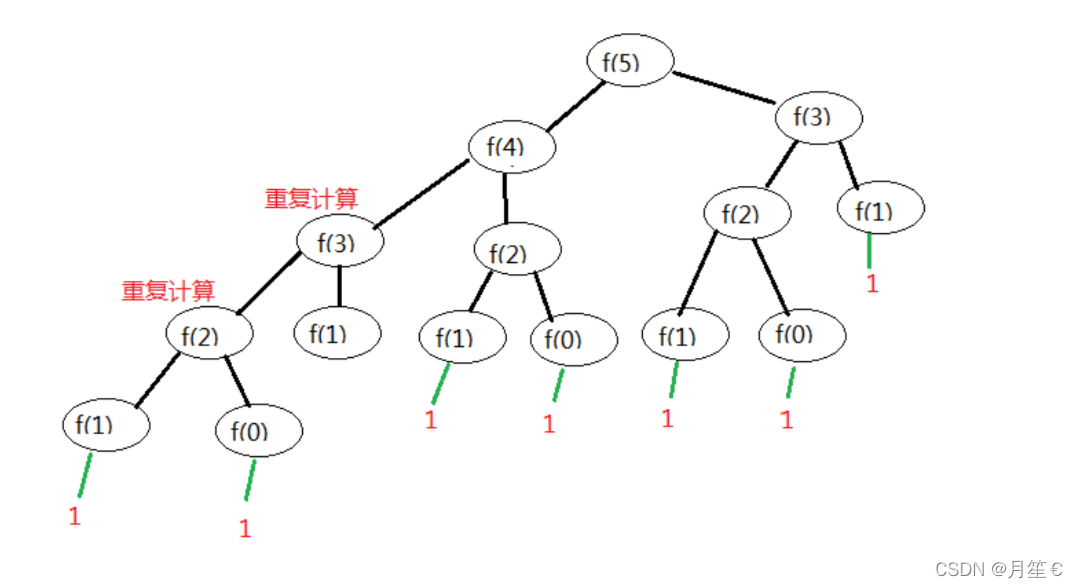
时间复杂度 O(2n),我们发现此算法的时间复杂度特别大,因为会进行大量的重复的计算,我们可以测验一下,当n如果特别大的时候,编译器要运行一段时间才会出结果,刚刚小编测验了一下,当n = 45的时候要运行几秒中才会出结果。
以 n = 5 为例 f(2) f(3) 都被重复计算多次,当然n越大,被重复计算的就会越多。
算法优化
既然上述算法中进行了大量的重复计算,时间复杂度为时间复杂度 O(2n),那么我们可以选择把计算过的结果保存下来,在这里考虑结果为方法数,用数组保存
- List item
就可以了。
代码如下:
public class TestDemo {
public static int climbStairs(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i < dp.length;i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
public static void main(String[] args) {
int res = climbStairs(5);
System.out.println("方法数:" + res);
}
}
运行结果:
因为数组中下标是从0开始的,但是我们的台阶数要从1开始,所以创建数组的时候开辟n + 1个空间大小。
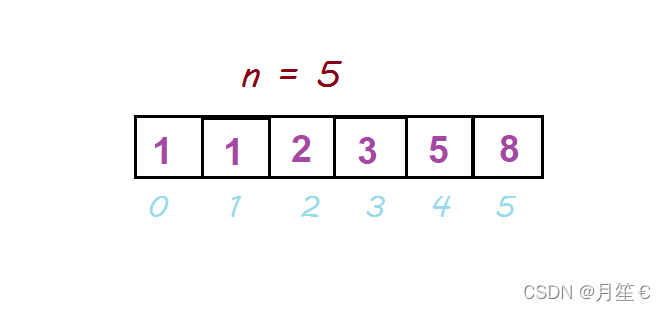
优化后的时间复杂度O(n)