优先队列

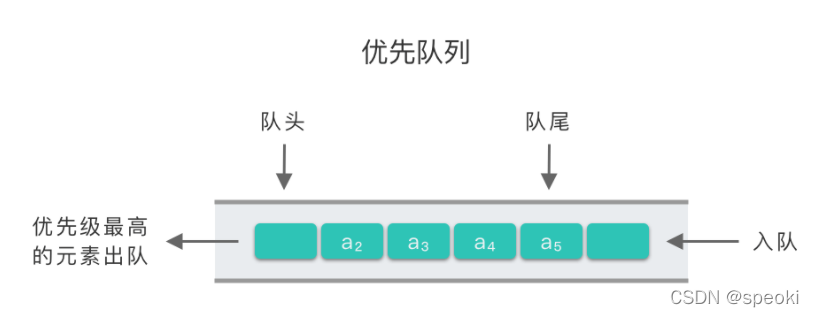
优先队列（Priority Queue）：一种特殊的队列。在优先队列中，元素被赋予优先级，当访问队列元素时，具有最高优先级的元素最先删除。

优先队列与普通队列最大的不同点在于出队顺序。

而优先队列的出队顺序跟入队顺序无关，优先队列是按照元素的优先级来决定出队顺序的。优先级高的元素优先出队，优先级低的元素后出队。优先队列符合「最高级先出（First in, Largest out）」的规则。

在这里插入图片描述

优先队列的适用场景

数据压缩：赫夫曼编码算法；
最短路径算法：Dijkstra 算法；
最小生成树算法：Prim 算法；
任务调度器：根据优先级执行系统任务；
事件驱动仿真：顾客排队算法；
选择问题：查找第 k 个最小元素。

很多语言都提供了优先级队列的实现。比如，Java 的 PriorityQueue，C++ 的 priority_queue 等。Python 中也可以通过 heapq 来实现优先队列。下面我们来讲解一下优先队列的实现。

优先队列的实现方法

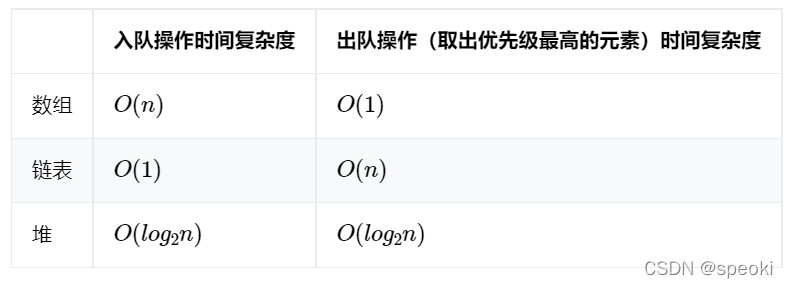
「数组（顺序存储）实现」
「链表（链式存储）实现」
「二叉堆结构实现」优先队列

在这里插入图片描述

二叉堆实现的优先队列

4.1 二叉堆的定义

二叉堆：符合以下两个条件之一的完全二叉树：

大顶堆：根节点值 ≥ 子节点值。
小顶堆：根节点值 ≤ 子节点值。

4.2 二叉堆的基本操作

「堆调整方法」和「将数组构建为二叉堆方法」

堆调整方法heapAdjust:
把移走了最大值元素以后的剩余元素组成的序列再构造为一个新的堆积。具体步骤如下：

从根节点开始，自上而下地调整节点的位置，使其成为堆积。即把序号为 i 的节点与其左子树节点（序号为 2 * i）、右子树节点（序号为 2 * i + 1）中值最大的节点交换位置。

因为交换了位置，使得当前节点的左右子树原有的堆积特性被破坏。于是，从当前节点的左右子树节点开始，自上而下继续进行类似的调整。

如此下去直到整棵完全二叉树成为一个大顶堆。

将数组构建为二叉堆的方法

如果原始序列对应的完全二叉树（不一定是堆）的深度为 d，则从 d - 1 层最右侧分支节点（序号为 ?n/2?）开始，初始时令 i = ?n/2?，调用堆调整算法。

每调用一次堆调整算法，执行一次 i = i - 1，直到 i == 1 时，再调用一次，就把原始数组构建为了一个二叉堆。

入队操作 heappush：
先将待插入元素 value 插入到数组 nums 末尾。
如果完全二叉树的深度为 d，则从 d - 1 层开始最右侧分支节点（序号为 ?n/2?）开始，初始时令 i = ?n/2?，从下向上依次查找插入位置。
遇到 value 小于当前根节点时，将其插入到当前位置。否则继续向上寻找插入位置。
如果找到插入位置或者到达根位置，将 value 插入该位置。
出队操作 heappop：
交换数组 nums 首尾元素，此时 nums 尾部就是值最大（优先级最高）的元素，将其从 nums 中弹出，并保存起来。
弹出后，对 nums 剩余元素调用堆调整算法，将其调整为大顶堆。

二叉堆实现优先队列

heapAdjust：将完全二叉树调整为二叉堆。
heapify：将数组构建为二叉堆方法（初始堆建立方法）。
heappush：向堆中添加元素，也是优先队列的入队操作。
heappop：删除堆顶元素，也是优先队列的出队操作，弹出优先队列中优先级最高的元素。
heapSort：堆排序。

Python使用heapq模块实现优先队列
Python中的heapq提供了优先队列算法，heapq.heappush()用在队列queue上插一个元素，heapq.heappop()用于在队列queue上删除一个元素
需要注意的是：heapq.heappop() 函数总是返回「最小的」的元素。所以我们在使用 heapq.heappush() 时，将优先级设置为负数，这样就使得元素可以按照优先级从高到低排序，这个跟普通的按优先级从低到高排序的堆排序恰巧相反。这样做的目的是为了 heapq.heappop() 每次弹出的元素都是优先级最高的元素。

import heapq

class PriorityQueue:
    def __init__(self):
        self.queue = []
        self.index = 0

    def push(self, item, priority):
        heapq.heappush(self.queue, (-priority, self.index, item))
        self.index += 1

    def pop(self):
        return heapq.heappop(self.queue)[-1]

优先队列的应用

滑动窗口的最大值

import heapq

class PriorityQueue:
    def __init__(self):
        self.queue = []
        self.index = 0

    def push(self, item, priority):
        heapq.heappush(self.queue, (-priority, self.index, item))
        self.index += 1

    def pop(self):
        return heapq.heappop(self.queue)[-1]

239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
//总窗口长度
PriorityQueue<int[]>pq = new PriorityQueue<int[]>(new Comparator<int[]>(){
    public int compare(int[] pair1,int[] pair2){
        return pair1[0]!=pair2[0]?pair2[0]-pair1[0]:pair2[1]-pair1[1];
        //如果不相等返回两个值的差，如果相等就返回两个index的差值
    }
});
//小的在前，大的在后
//构造优先队列
for(int i=0;i<k;i++){
    pq.offer(new int[]{nums[i],i});
    //放入元素
}
//返回滑动窗口的最大值
//将窗口向右滑动
//
int []ans = new int[n-k+1];
ans[0]=pq.peek()[0];

for(int i=k;i<n;++i){
  //放入当前滑动窗口的最大值
    pq.offer(new int[]{nums[i],i});

    while(pq.peek()[1]<=i-k){
pq.poll();
//将元素index小于等于i-k的pop出来
    }
    ans[i-k+1]=pq.peek()[0];
    //最大值存入 
}
return ans;

    }
}

347 前k个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按任意顺序返回答案。

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
int len = nums.length;
Map<Integer,Integer> total = new HashMap<Integer,Integer>();
for(int num:nums){
total.put(num,total.getOrDefault(num,0)+1);
}
//辅助数据结构
PriorityQueue<int[]>pq = new PriorityQueue<int[]>(new Comparator<int[]>(){
    public int compare(int[] pair1,int[] pair2){ 
        return pair1[1]-pair2[1];
      //出现次数的差值
    }
});
for(Map.Entry<Integer,Integer>entry:total.entrySet()){
    int num = entry.getKey(),count = entry.getValue();
    //如果当前队列的大小等于k，要将大小保持在k
    if(queue.size()==k){
        if(queue.peek()[1]<count){
            //如果第一个元素频率小于得到的键值，就将元素pop出来
            queue.poll();
            //刷新元素
            queue.offer(new int[]{num,count});
        }
    }else{
        
        queue.offer(new int[]{num,count});
    }
}

//答案
int []ret = new int[k];
for(int i=0;i<k;++i){
    ret[i]=queue.poll()[0];
}
return ret;
    }
}

451. 根据字符出现频率排序

给定一个字符串，请将字符串里的字符按照出现的频率降序排列。

输入:
“tree”

输出:
“eert”

解释:
'e’出现两次，'r’和’t’都只出现一次。
因此’e’必须出现在’r’和’t’之前。此外，"eetr"也是一个有效的答案。

class Solution {
    public String frequencySort(String s) {
int len = s.length();
Map<Character,Integer> total= new HashMap<Character,Integer>();
//辅助数据结构
for(char c:s.toCharArray()){
total.put(c,total.getOrDefault(c,0)+1);
}
PriorityQueue<HashMap.Entry<Character,Integer>> pq = new PriorityQueue<>((a, b) -> (Integer)b.getValue() - (Integer)a.getValue());
        
for (Map.Entry<Character, Integer> entry: total.entrySet()) {
            pq.offer(entry);
}
        
    //放入元素

StringBuffer sb = new StringBuffer();
int size = pq.size();
for(int i=0;i<size;i++){
   Map.Entry<Character,Integer> top = pq.poll();
    char c = top.getKey();
  int f = top.getValue();
    for(int j=0;j<f;j++){
        sb.append(c);
    }

}
return sb.toString();
    }   
}