数据结构


数组或列表

数组
对于数组,比如C语言或者python的一些模块,他们要求数据类型相同,有固定的长度,因此在存储时会根据存储的类型进行取值。举个例子,一个数组a里面存储了一堆int类型的数字如1 2 3,一个int类型占4个字节,那么如果a[0]的地址是100,a[1]的地址便是104,a[2]的地址便是108,其分别指向的数字便是 1 2 3。
列表
而对于python的列表,它可以存储各种类型的元素如 1 ‘nihao’ False 等,每种类型的元素所占字节数大都不相同,所以python列表内存储的则是各个元素的地址,如地址是100的a[0]存储的数据为整形地址123,地址是104的a[1]存储的数据为整形地址456...其分别指向的元素是地址为123的1,地址为456的‘nihao’,地址为789的 False。 当然这里的地址和地址类型只是用来举个例子。
python的列表不需要设置长度/空间,实际上在python底层,每次经过append等的方式使数组变长且超过新设定的空间时,系统会重新开辟一块更大的空间用来存放这个数组里的东西,把之前的数组里的元素拷贝进去。
对于列表的append操作时间复杂度是O(1),像remove,insert则为O(n),因为每执行一次,第一步先找到他,第二步删除且其后面的元素的索引都会发生改变。当然也要考虑当remove,insert处理的是最后一个元素的时候。这里指平均。
栈

我们用python代码简单模拟一下栈的操作流程
class Stack:
def __init__(self):
self.stack = []
def push(self, element):
self.stack.append(element)
def pop(self):
if not self.is_empty():
return self.stack.pop()
else:
raise IndexError('stack is empty!!!')
def get_top(self):
if self.is_empty():
return None
else:
return self.stack[-1]
def is_empty(self):
return True if len(self.stack) == 0 else False
stack = Stack()
for i in range(5):
stack.push(i)
print(stack.stack)
for i in range(5):
print(stack.pop())
队列

到了队列,便会出现一个问题,我们在列表中每删除一个元素,其后面的元素都会向前移动,这样变导致十分麻烦,那么该如何解决这个问题呢?
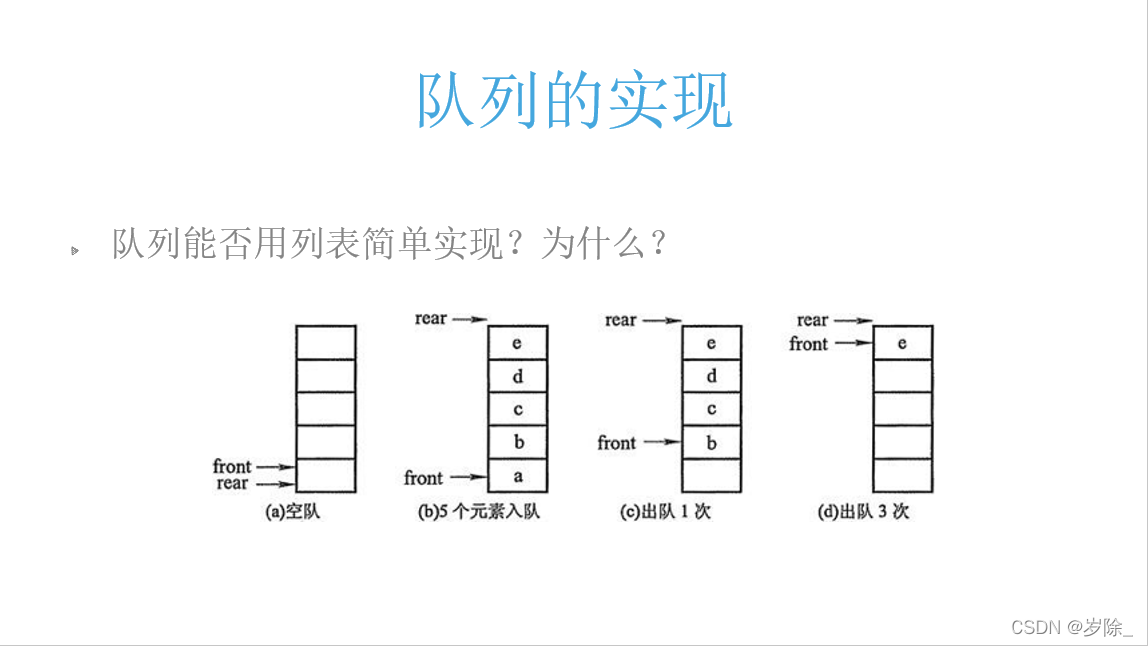
显然,若是通过移动front所指的位置,便可避免上面所说的情况,但新的问题又出现了,在其他语言里,数组的长度是固定的,此时我若是再想填充数据,前面的空间浪费,后面的空间又不够,该如何是好呢?
于是我们引出环形队列

从图中可以看出以下规律:

长度为12最多存11条数据
该队列可以转着圈地加或者删除,直到(rear+1)%MaxSize==front队满或者rear==front?队空
每完成一圈都要回到原点所以用取余地方式完成
python代码简单实现以下队列:
class Queue:
def __init__(self, size=12):
self.queue = [0 for _ in range(size)] #模拟长度固定
self.size = size
self.front = 0
self.rear = 0
def push(self, element):
if not self.is_filled():
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = element
else:
raise IndexError('out of range!!!')
def pop(self):
if not self.is_empty():
self.front = (self.front + 1) % self.size
return self.queue[self.front]
else:
return None #当然抛出异常也行这里为了方便就这样写了
def is_empty(self):
return True if len(self.queue) == 0 else False
def is_filled(self):
return True if (self.rear + 1) % self.size == self.front else False
q = Queue()
for i in range(5, 16): #再多就会报错
q.push(i)
print(q.queue) # [0, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
for i in range(5):
print(q.pop())
双向队列:

?python的队列内置模块
在以前学习的进程间的数据共享时学到过一个queue,这个虽是队列,但其作用是为保证数据安全的。
在python内 collections有一些数据结构 如deque表示双向队列
from collections import deque
q = deque()
# q = deque([1,2,3])
# 当然也可以设置最大长度 q = deque([1,2,3], 5)
# 但队满了再加不会报错 而是前一个自动出队
q.append(1) #队尾进队
print(q.popleft()) #队首出队 没有报错
q.appendleft(22) #队首进队
print(q.pop()) #队尾出队 没有报错当然如果只用前两条append popleft那也可以当成一个单向队列
这里不仅可以放一个数组,还可以放一个比如文件对象,q=deque(f,5)这样就能获取该文件最后五行内容。
栈和队列的应用--迷宫问题
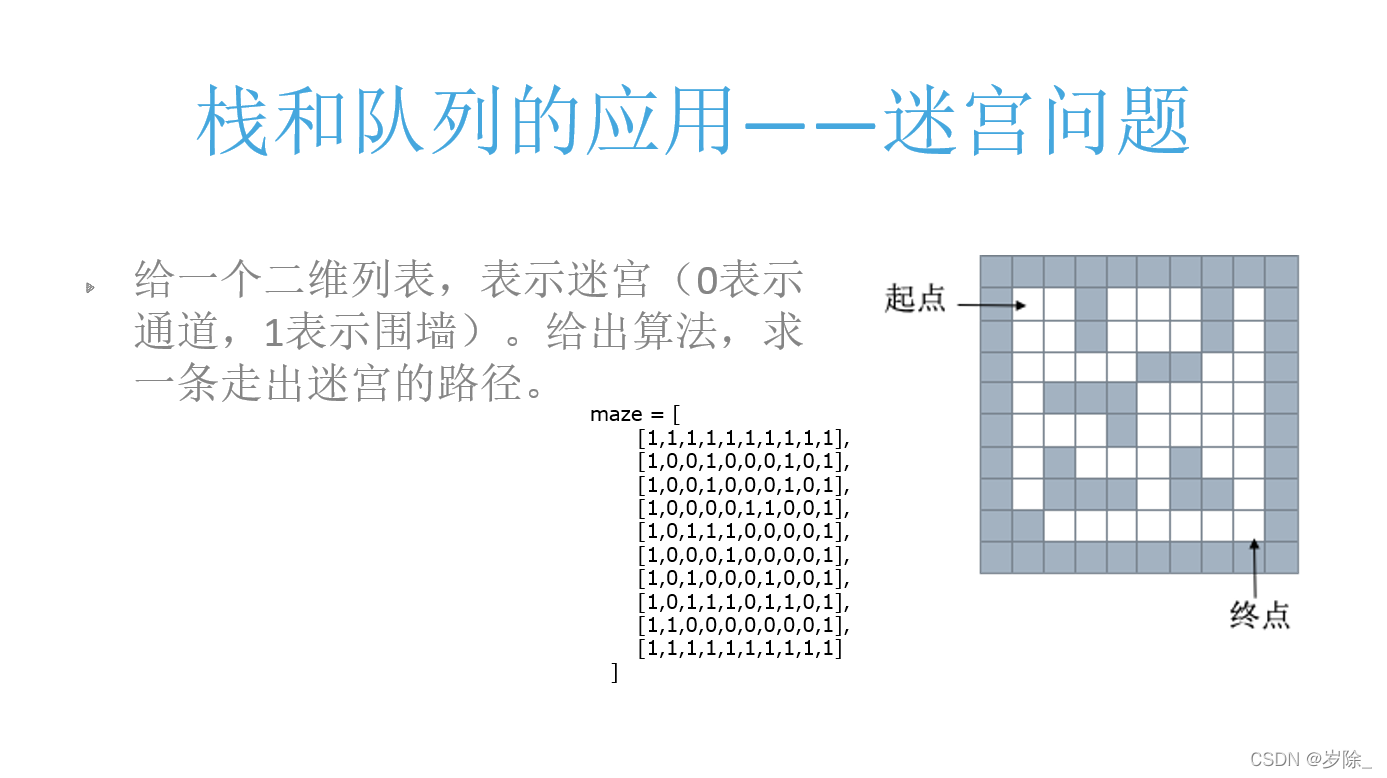
栈?
深度优先搜索,一条路走到黑,也叫回溯法。

?代码实现:
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x, y - 1),
]
def maze_path(x1, y1, x2, y2):
stack = [(x1, y1)]
while len(stack) > 0:
curNode = stack[-1]
if curNode == (x2, y2):
return stack
for dir in dirs: # 四个方向
nextNode = dir(curNode[0], curNode[1])
if maze[nextNode[0]][nextNode[1]]==0:
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]] = 2 # 表示走过
break
else:
maze[nextNode[0]][nextNode[1]] = 2
stack.pop()
else: # 没有路
return False
print(maze_path(1,1,8,8))
# [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (6, 3), (6, 4), (6, 5), (7, 5), (8, 5), (8, 6), (8, 7), (8, 8)]
使用队列求出最短路径:
广度优先搜索

?当我们找到终点时,因为我们最后求的是路径,所以可以再开辟一个列表,从终点开始往前找,来存当前和来自的位置。
from collections import deque
maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
[1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
[1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
[1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]
dirs = [
lambda x, y: (x + 1, y),
lambda x, y: (x - 1, y),
lambda x, y: (x, y + 1),
lambda x, y: (x, y - 1),
]
def realPath(path):
curNode = path[-1]
realpath = []
while curNode[2] != -1:
realpath.append(curNode[0:2])
curNode = path[curNode[2]]
realpath.append(curNode[0:2])
realpath.reverse()
return realpath
def maze_path_queue(x1, y1, x2, y2):
q = deque()
path = []
q.append((x1, y1, -1))
while len(q):
curNode = q.popleft()#队首出队
path.append(curNode)
if curNode[0] == x2 and curNode[1] == y2:
real_path = realPath(path)
return real_path
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
if maze[nextNode[0]][nextNode[1]] == 0:
maze[nextNode[0]][nextNode[1]] = 2
q.append((nextNode[0], nextNode[1], len(path)-1)) #len(path)-1 为path最后一个元素的索引
else:
print('没有路')
return None
print(maze_path_queue(1, 1, 8, 8))
# [(1, 1), (2, 1), (3, 1), (4, 1), (5, 1), (5, 2), (5, 3), (6, 3), (6, 4), (6, 5), (7, 5), (8, 5), (8, 6), (8, 7), (8, 8)]可以看到,该方法与使用栈的方法结果路径一致,实际上这是一种巧合,上面栈的方法是按照下上右左的顺序走的,刚好实现最短路径。同时,虽然队列的方法可以找到相对应的最短路径,但未必真的就是最短,因为可以有的格子被前一步占用了。
像一些其他问题,比如一个机器人只会向右或者向下走,也可以通过上面的方法变形改一下dirs,问有多少条路径,那函数里面就不要写死,但这样只适用于小型数据,其实这样的题还有更简单的方法,后面再说。
链表
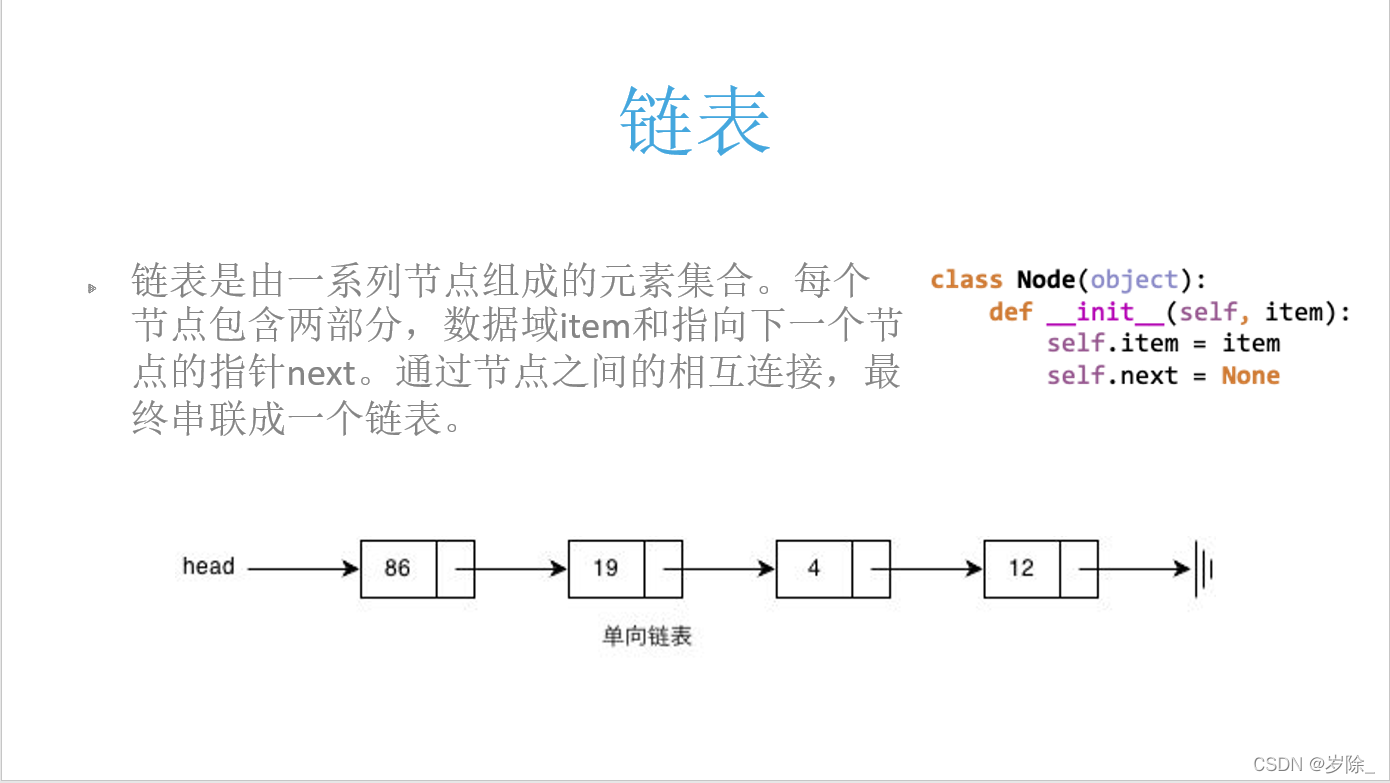
代码实现:
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 头插法
def create_linklist_head(li):
head = Node(li[0])
for element in li[1:]:
node = Node(element)
node.next = head
head = node
return head
# 尾插法
def create_linklist_tail(li):
head = Node(li[0])
t = head
for element in li[1:]:
node = Node(element)
t.next = node
t = node
return head
# 遍历链表
def print_linklist(head):
while head:
print(head.item, end=',')
head = head.next
# 中间插入一个节点 为方便 num为第num个而不是从0开始 令count=1
# 存在一定问题 None.next会报错 可以加个判断 其实正常也不用这样写 下同
def ins_node(head,num,node):
t = head
count = 1
while t:
if count == num - 1:
node.next = t.next
t.next = node
break
t = t.next
count += 1
return head
# 删除第num个节点 这里第一个节点从1开始
def del_node(head, num):
t = head
count = 1
while t:
if count == num - 1:
t.next = t.next.next
break
t = t.next
count += 1
return head
# 当然只在最前面或者最后面插入一个元素也可以 可以用再写一份前后插入一个元素
# 这样的方式可以假如也可从根据列表创建链表
print_linklist(create_linklist_head([1, 2, 3, 4, 5]))
print('')
print_linklist(create_linklist_tail([1, 2, 3, 4, 5]))
print('')
print_linklist(ins_node(create_linklist_tail([1, 2, 3, 4, 5]), 2, Node(999))) #第二个节点插入为999
print('')
print_linklist(del_node(create_linklist_tail([9, 10, 1, 2, 3, 4, 5]), 3)) # 删除第三个节点1
#也可以再写一个函数 用来删除某个元素 而不是像上面根据位置删除
# 5,4,3,2,1,
# 1,2,3,4,5,
# 1,999,2,3,4,5,
# 9,10,2,3,4,5,?封装到类中,使链表可以像列表一样直接遍历或者可以调用一些方法。
# 链表
class LinkList:
# 节点
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 迭代器
class LinkListIterator:
def __init__(self, node):
self.node = node
def __next__(self):
if self.node:
cur_node = self.node
self.node = cur_node.next
return cur_node.item
else:
raise StopIteration
def __iter__(self):
return self
# 链表功能
def __init__(self, iterable=None):
self.head = None
self.tail = None
if iterable:
self.extend(iterable)
def append(self, obj):
s = LinkList.Node(obj)
if not self.head:
self.head = s
self.tail = s
else:
self.tail.next = s
self.tail = s
def extend(self, iterable):
for obj in iterable:
self.append(obj)
def find(self, obj):
for n in self: # self为 << 111,444,222,3,5,7>>
if n == obj:
return True
else:
return False
def __iter__(self):
return self.LinkListIterator(self.head) # 可迭代对象
def __repr__(self):
return "<< " + ",".join(map(str, self)) + ">>"
lst = [3, 5, 7]
l = LinkList([111,444])
l.append(222)
l.extend(lst)
print(l.__repr__())
print(l)
for i in l:
print(i)
print(l.find(3))
print(5 in l)
'''
<< 111,222,3,5,7>>
<< 111,222,3,5,7>>
111
222
3
5
7
True
True
'''?双链表: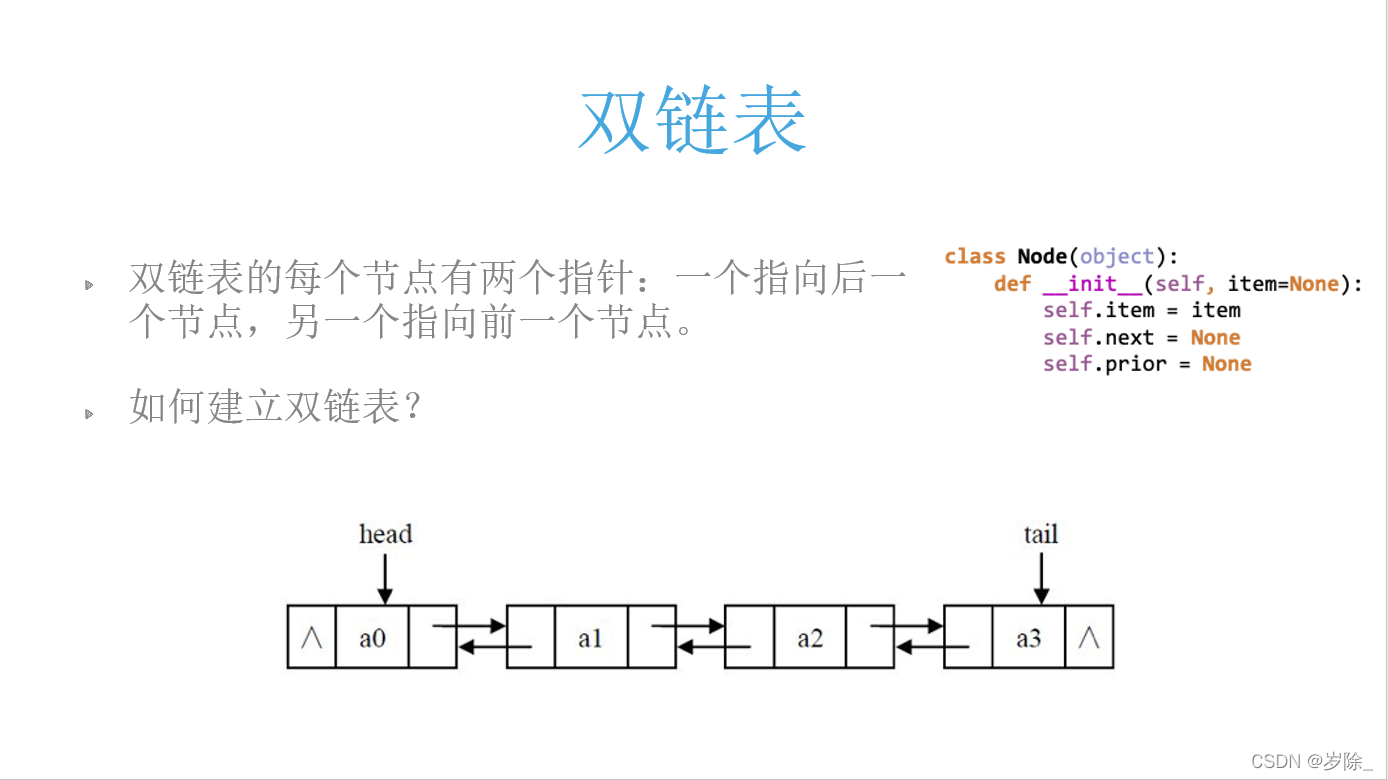
?大同小异 不再进行展示

?
前面讲的栈和队列都可以用链表(单项或者双向)实现,且更快捷。比如队列可以弄一个链表,甚至不用环形了,进一个出一个。
链表的增删不会像列表一样影响到后面的变化。
哈希表
python的字典和集合就是通过哈希表实现的

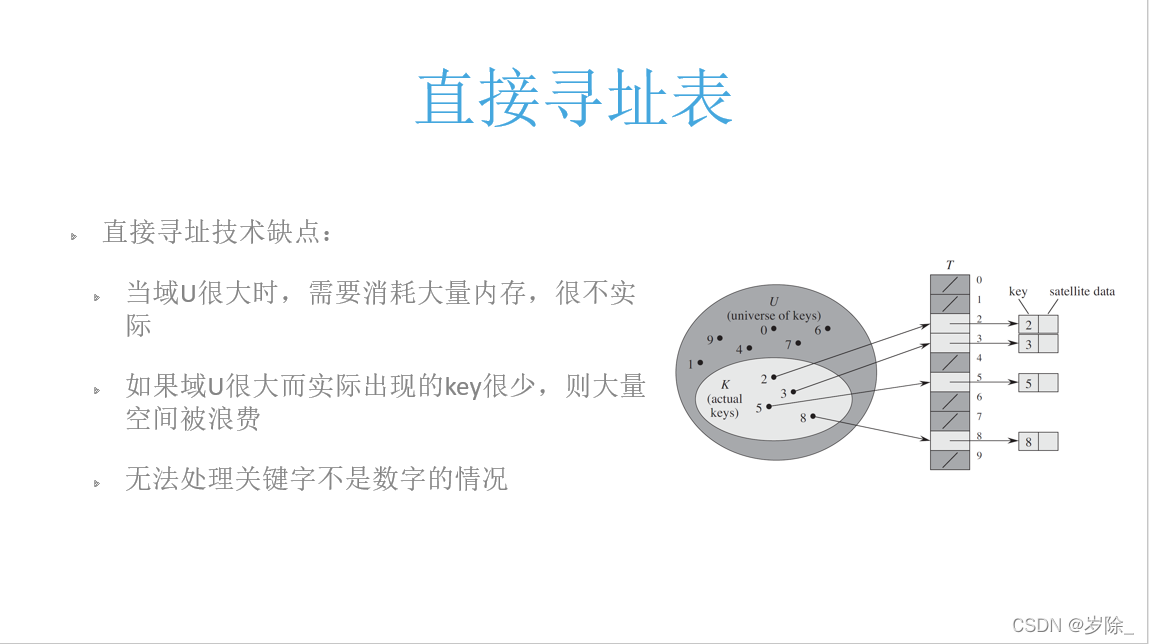
首先 来认识一下直接寻址表?
 ??
??
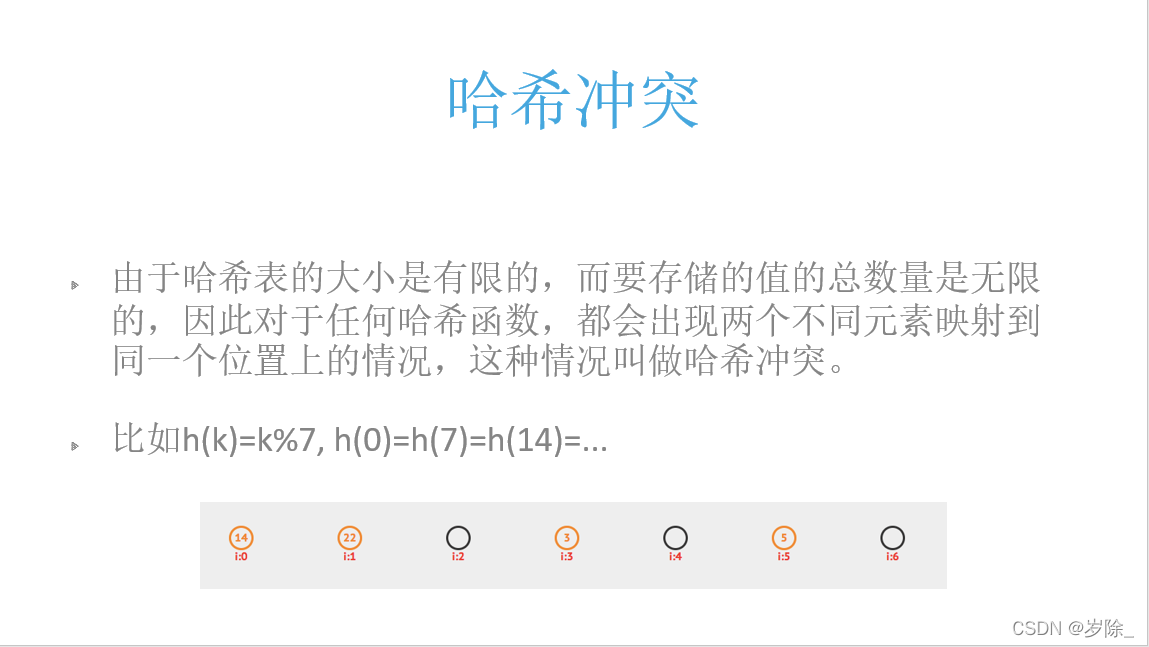
?哈希

哈希表 = 哈希 + 直接寻址表
 ?这样存储便出现一个问题,如数字14 和 21 都会存储在
?这样存储便出现一个问题,如数字14 和 21 都会存储在![]() 位置上
位置上
?
?于是

但这样都不是很完美,像第一种,涉及一些密度过大,装载因子过大等问题。
也有可能哈希表满了就无法再装了。
 ?比如我要寻找171这个数字,那么它就会在11号链表中寻找,91、155、直到找到第三个171。
?比如我要寻找171这个数字,那么它就会在11号链表中寻找,91、155、直到找到第三个171。
python代码简单实现哈希表
注:类似于集合的结构,所以键不会重复,这里就不加限制了。更高级一点的还可以加个count参数用来计数出现的次数。
? ? ? ? 本哈希函数用的取模法,如果进来的是字符串等的可以加个进制编码转换,转换成数字如md5加密等,这里就不写了。
? ? ? ? 删除功能也还没写,要记得在上面链表里也加上删除功能。
# 链表
class LinkList:
# 节点
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 迭代器
class LinkListIterator:
def __init__(self, node):
self.node = node
def __next__(self):
if self.node:
cur_node = self.node
self.node = cur_node.next
return cur_node.item
else:
raise StopIteration
def __iter__(self):
return self
# 链表功能
def __init__(self, iterable=None):
self.head = None
self.tail = None
if iterable:
self.extend(iterable)
def append(self, obj):
s = LinkList.Node(obj)
if not self.head:
self.head = s
self.tail = s
else:
self.tail.next = s
self.tail = s
def extend(self, iterable):
for obj in iterable:
self.append(obj)
def find(self, obj):
for n in self:
if n == obj:
return True
else:
return False
def __iter__(self):
return self.LinkListIterator(self.head) # 可迭代对象
def __repr__(self):
return "<< " + ",".join(map(str, self)) + ">>"
# 哈希表
class HashTable:
def __init__(self, size=6):
self.size = size
self.T = [LinkList() for _ in range(size)]
def h(self, k):
return k % self.size
def insert(self, k):
i = self.h(k)
if self.find(k):
print('Duplicated Insert')
else:
self.T[i].append(k)
def find(self, k):
i = self.h(k)
return self.T[i].find(k)
ht = HashTable()
ht.insert(0)
ht.insert(1)
ht.insert(2)
ht.insert(101)
ht.insert(102)
print(ht.find(3)) # False
print(ht.T) # [<< 0,102>>, << 1>>, << 2>>, << >>, << >>, << 101>>]


 ?
?
?

树与二叉树
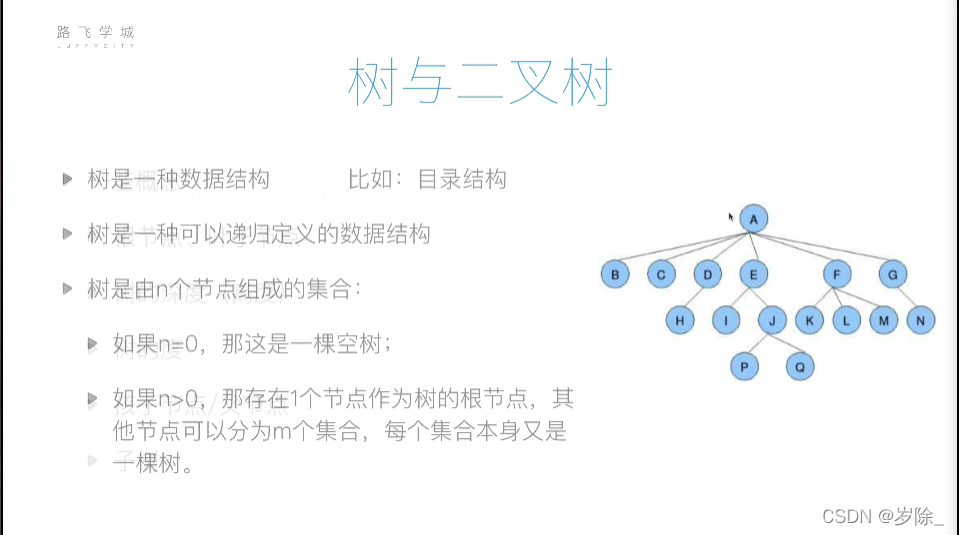
?
二叉树
度不超过2的树
二叉树的线性存储方式:
存放到列表里 2i+1 2i+2 适合完全二叉树
self.children = []
二叉树的链式存储方式:
提前上代码
from collections import deque
class BiTreeNode:
# 初始化每个节点
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
class BST:
def __init__(self, tree_list=None):
self.root = None
# 用来存放某子树的升序排列
if tree_list:
for i in tree_list:
self.insert_no_rec(i)
# 递归插入 不考虑等于 下同
def insert(self, node, val):
if not node:
node = BiTreeNode(val)
elif val < node.data:
node.lchild = self.insert(node.lchild, val)
node.lchild.parent = node
elif val > node.data:
node.rchild = self.insert(node.rchild, val)
node.rchild.parent = node
return node
# 非递归插入 一般来说快一点
def insert_no_rec(self, val):
n = self.root
if not n:
self.root = BiTreeNode(val)
return
while True:
if val < n.data:
if n.lchild:
n = n.lchild
else:
n.lchild = BiTreeNode(val)
n.lchild.parent = n
return
elif val > n.data:
if n.rchild:
n = n.rchild
else:
n.rchild = BiTreeNode(val)
n.rchild.parent = n
return
else:
return
# 前序遍历
def pre_order(self, root):
if root:
print(root.data, end=' ')
self.pre_order(root.lchild)
self.pre_order(root.rchild)
# 中序遍历
def in_order(self, root):
if root:
self.in_order(root.lchild)
print(root.data, end=' ')
self.in_order(root.rchild)
# 中序遍历 迭代法
def inorderTraversal(self, root):
res = []
stack = []
while stack or root:
# 不断往左子树方向走,每走一次就将当前节点保存到栈中
# 这是模拟递归的调用
if root:
stack.append(root)
root = root.lchild
# 当前节点为空,说明左边走到头了,从栈中弹出节点并保存
# 然后转向右边节点,继续上面整个过程
else:
tmp = stack.pop()
res.append(tmp.data)
root = tmp.rchild
return res
# 后序遍历
def post_order(self, root):
if root:
self.post_order(root.lchild)
self.post_order(root.rchild)
print(root.data, end=' ')
# 层级遍历
def level_order(self, root):
q = deque()
q.append(root)
while q:
node = q.popleft()
print(node.data, end=' ')
if node.lchild:
q.append(node.lchild)
if node.rchild:
q.append(node.rchild)
# 递归查询
def query(self, node, val):
if not node:
return None
if val < node.data:
return self.query(node.lchild, val)
elif val > node.data:
return self.query(node.rchild, val)
else:
return node
# 非递归查询
def query_no_rec(self, val):
n = self.root
while n:
if val < n.data:
n = n.lchild
elif val > n.data:
n = n.rchild
else:
return n
# 子树升序
def sorted_tree_list(self, root):
sorted_list = []
def inner(root):
if root:
inner(root.lchild)
sorted_list.append(root.data)
inner(root.rchild)
inner(root)
return sorted_list
# 删除情况1
def __del_node_1(self, node):
# 如果是根节点 更新根节点 下同
if not node.parent:
self.root = None
if node.parent.lchild == node:
node.parent.lchild = None
elif node.parent.rchild == node:
node.parent.rchild = None
# 删除情况2
def __del_node_2(self, node):
next_node = node.lchild or node.rchild
next_node.parent = node.parent
if not node.parent:
self.root = next_node
if node.parent.lchild == node:
node.parent.lchild = next_node
else:
node.parent.rchild = next_node
# 删除情况3
def __del_node_3(self, node):
min_node = node.rchild
while min_node.lchild:
min_node = min_node.lchild
node.data = min_node.data
# 删除情况1
if not (min_node.lchild or min_node.rchild):
self.__del_node_1(min_node)
# 删除情况2
elif not (min_node.lchild and min_node.rchild):
self.__del_node_2(min_node)
# 删除某个值
def delete(self, val):
# 根据值取找节点
node = self.query_no_rec(val)
# 如果不在树里
if not node:
raise ValueError('tree.del_node(x): x not in tree')
# 删除情况1
if not (node.lchild or node.rchild):
self.__del_node_1(node)
# 删除情况2
elif not (node.lchild and node.rchild):
self.__del_node_2(node)
# 删除情况3
else:
self.__del_node_3(node)
li = [17, 5, 25, 35, 2, 11, 9, 7, 8, 29, 38, 16]
tree = BST(li)
tree.level_order(tree.root)
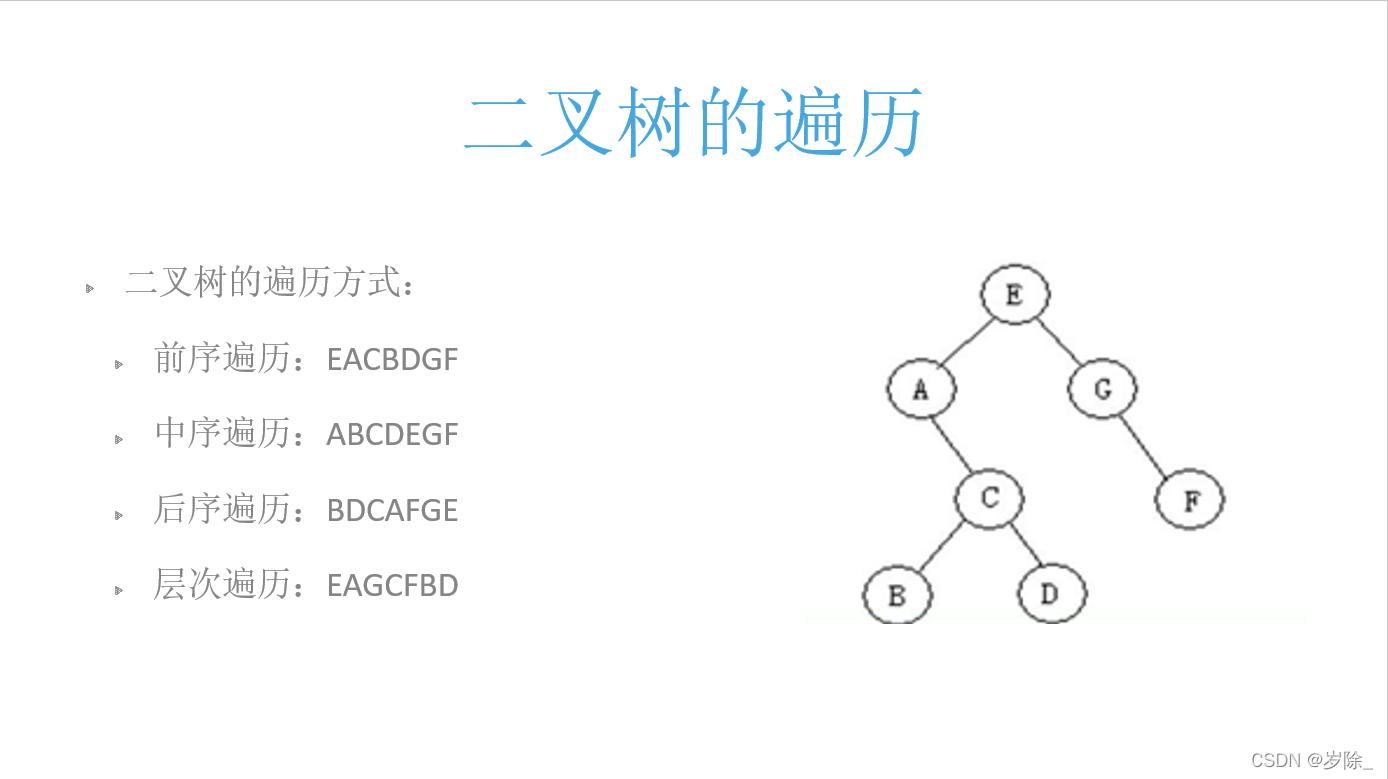
手动创建上图这棵树:
class BiTreeNode:
# 初始化每个节点
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
# self.parent = None
a = BiTreeNode('A')
b = BiTreeNode('B')
c = BiTreeNode('C')
d = BiTreeNode('D')
e = BiTreeNode('E')
f = BiTreeNode('F')
g = BiTreeNode('G')
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f
root = e
?二叉树遍历:
# 前序遍历
def pre_order(root):
if root:
print(root.data, end=' ')
pre_order(root.lchild)
pre_order(root.rchild)
# 中序遍历
def in_order(root):
if root:
in_order(root.lchild)
print(root.data, end=' ')
in_order(root.rchild)
# 后序遍历
def post_order(root):
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.data, end=' ')
# 层次遍历
def level_order(root):
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data, end=' ')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
pre_order(root)
print('')
in_order(root)
print('')
post_order(root)
print('')
level_order(root)
print('')
'''
E A C B D G F
A B C D E G F
B D C A F G E
E A G C F B D
'''注意:给出一个棵树的两种遍历,要会还原出这棵树。也要会各种遍历的规律。
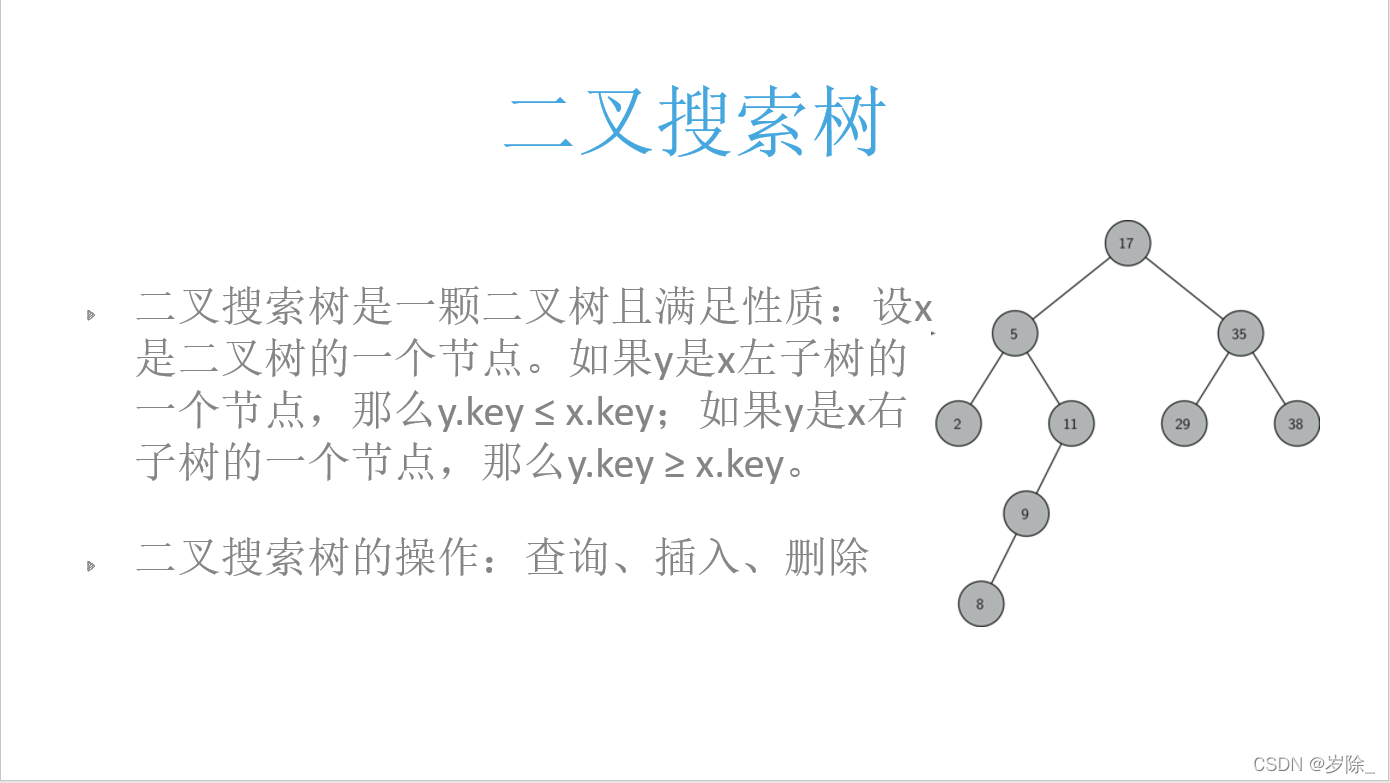
import random
from collections import deque
class BiTreeNode:
# 初始化每个节点
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
class BST:
def __init__(self, li=None):
self.root = None
if li:
for i in li:
self.insert_no_rec(i)
# 不考虑等于 当然也可以放左边或者右边或者计数但没必要
# 递归插入
def insert(self, node, val):
if not node:
node = BiTreeNode(val)
elif val < node.data:
node.lchild = self.insert(node.lchild, val)
node.lchild.parent = node
elif val > node.data:
node.rchild = self.insert(node.rchild, val)
node.rchild.parent = node
return node
# 非递归插入 一般来说快一点
def insert_no_rec(self, val):
n = self.root
if not n:
self.root = BiTreeNode(val)
return
while True:
if val < n.data:
if n.lchild:
n = n.lchild
else:
n.lchild = BiTreeNode(val)
n.lchild.parent = n
return
elif val > n.data:
if n.rchild:
n = n.rchild
else:
n.rchild = BiTreeNode(val)
n.rchild.parent = n
return
else:
return
def pre_order(self,root):
if root:
print(root.data, end=' ')
self.pre_order(root.lchild)
self.pre_order(root.rchild)
def level_order(self, root):
q = deque()
q.append(root)
while q:
node = q.popleft()
print(node.data, end=' ')
if node.lchild:
q.append(node.lchild)
if node.rchild:
q.append(node.rchild)
li = [17, 5, 35, 2, 11, 9, 8, 29, 38]
tree = BST(li) #这里init方法调用了insert_no_rec初始化了tree.root不再是None了
tree.insert(tree.root, 1)
tree.insert_no_rec(3)
tree.pre_order(tree.root) # 17 5 2 1 3 11 9 8 35 29 38
print('')
tree.level_order(tree.root) # 17 5 35 2 11 29 38 1 3 9 8
中序遍历的二叉搜索树是有序的(先左再自己再右)
l = list(range(1, 11))
random.shuffle(l)
tree1 = BST(l)
tree1.in_order(tree1.root)
# 1 2 3 4 5 6 7 8 9 10 ?查询:
# 递归查询
def query(self, node, val):
if not node:
return None
if val < node.data:
return self.query(node.lchild, val)
elif val > node.data:
return self.query(node.rchild, val)
else:
return node
# 非递归查询
def query_no_rec(self,val):
n = self.root
while n:
if val < n.data:
n = n.lchild
elif val > n.data:
n = n.rchild
else:
return n
print(tree.query(tree.root, 5))
print(tree.query_no_rec(38))
'''
<__main__.BiTreeNode object at 0x0000024C5029FBB0>
<__main__.BiTreeNode object at 0x0000024C502B8250>
'''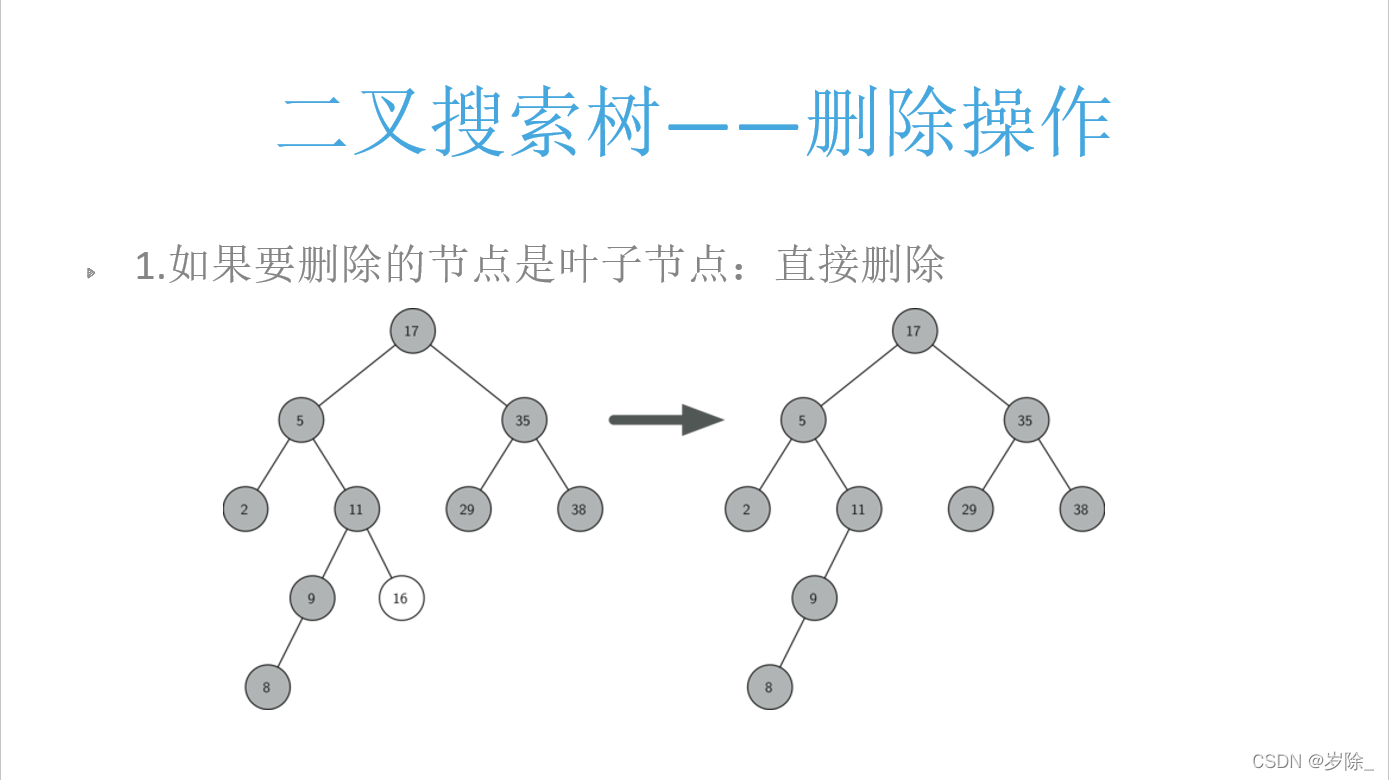
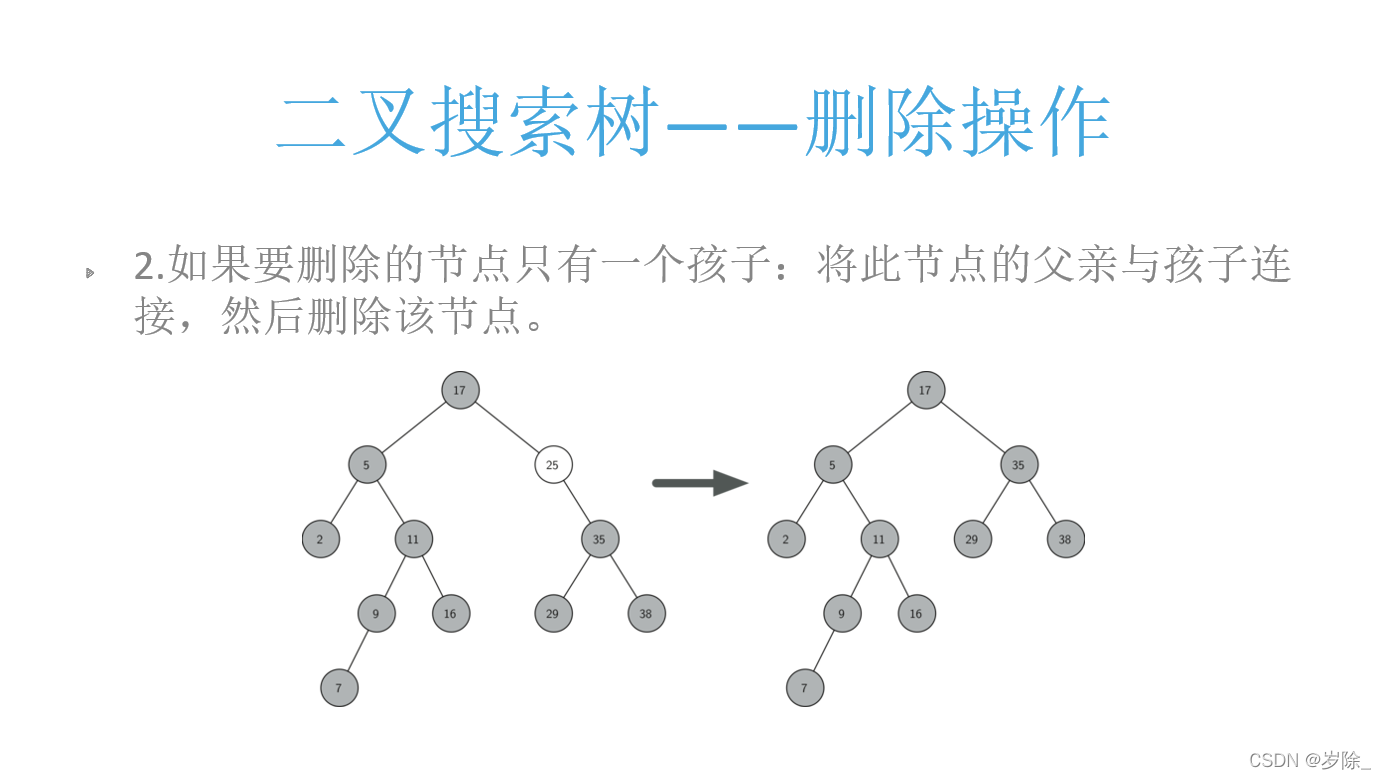
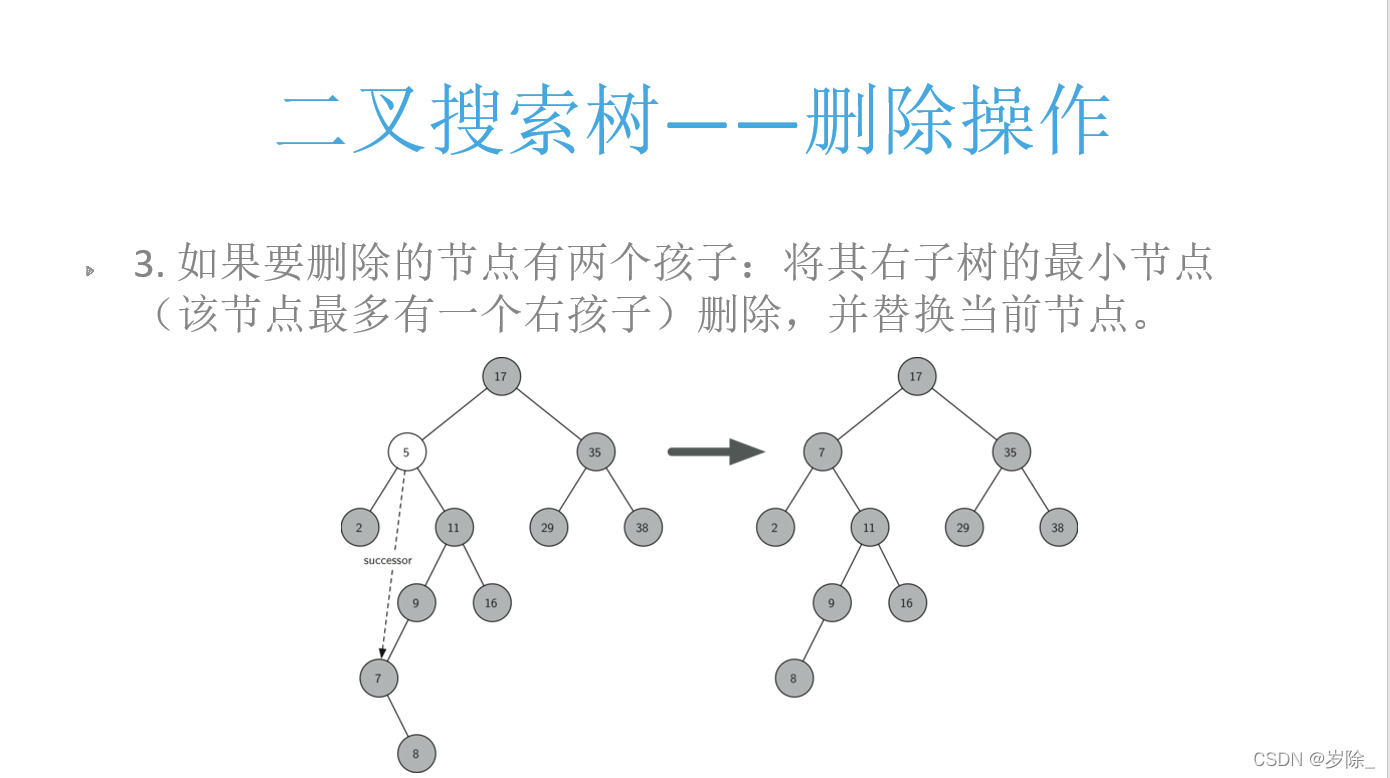
删除:?
我们构造一个图2这种情况的树,即包含要删除的点16 25 5
from collections import deque
class BiTreeNode:
# 初始化每个节点
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
class BST:
def __init__(self, li=None):
self.root = None
self.__sorted_list = []
if li:
for i in li:
self.insert_no_rec(i)
def level_order(self, root):
q = deque()
q.append(root)
while q:
node = q.popleft()
print(node.data, end=' ')
if node.lchild:
q.append(node.lchild)
if node.rchild:
q.append(node.rchild)
def __sorted_tree_list(self, root):
if root:
self.__sorted_tree_list(root.lchild)
self.__sorted_list.append(root)
self.__sorted_tree_list(root.rchild)
def del_node(self, val):
node = self.query_no_rec(val)
# 如果不在树里
if not node:
raise ValueError('tree.del_node(x): x not in tree')
# 删除情况1
if not (node.lchild or node.rchild):
# 如果是根节点 更新根节点 下同
if not node.parent:
self.root = None
if node.parent.lchild == node:
node.parent.lchild = None
elif node.parent.rchild == node:
node.parent.rchild = None
# 删除情况2
elif not (node.lchild and node.rchild):
next_node = node.lchild or node.rchild
next_node.parent = node.parent
if not node.parent:
self.root = next_node
if node.parent.lchild == node:
node.parent.lchild = next_node
else:
node.parent.rchild = next_node
# 删除情况3
else:
self.__sorted_tree_list(node.rchild)
# 这个change节点肯定是其父节点的左孩子 或 开始寻找的第一个右节点(初始分支此时没有左)
change_node = self.__sorted_list[0]
# 这里直接改变data值 所以该node父子关系不变 self.root依然指向根节点
node.data = change_node.data
# 这个change节点是其父节点的左孩子(change右边第一个节点有左孩子)
if change_node.parent.lchild == change_node:
if change_node.rchild:
change_node.parent.lchild = change_node.rchild
change_node.rchild.parent = change_node.parent
else:
change_node.parent.lchild = None
# 开始寻找的第一个右节点(change右边第一个节点没左孩子)
# 此时其实就是node和node的右孩子的右孩子进行拼接
elif change_node.parent.rchild == change_node:
# change节点如果有右孩子
if change_node.rchild:
change_node.parent.rchild = change_node.rchild
change_node.rchild.parent = change_node.parent
# change节点如果没有右孩子
else:
change_node.parent.rchild = None
li = [17, 5, 25, 35, 2, 11, 9, 7, 8, 29, 38, 16]
tree = BST(li)
tree.level_order(tree.root)
print('\n删除16:')
tree.del_node(16)
tree.level_order(tree.root)
print('\n删除25:')
tree.del_node(25)
tree.level_order(tree.root)
print('\n删除5:')
tree.del_node(5)
tree.level_order(tree.root)
'''
17 5 25 2 11 35 9 16 29 38 7 8
删除16:
17 5 25 2 11 35 9 29 38 7 8
删除25:
17 5 35 2 11 29 38 9 7 8
删除5:
17 7 35 2 11 29 38 9 8
'''注:该删除仅代表思路,最上方二叉树刚开始时有完整代码优化。

要会写一些算法,如两个二叉树是否相同,前中后序层级遍历的不同输出方式或者迭代递归法完成。给出一数组生成可能的树等等。。