
模型介绍:
值得注意的是,特殊因子是不能被公共因子包含的。


载荷矩阵的几个统计性质:




下面通过一个例题来展示。


ssgs = [43.31 7.39 8.73 54.89 15.35
17.11 12.13 17.29 44.25 29.69
21.11 6.03 7 89.37 13.82
29.55 8.62 10.13 73 14.88
11 8.41 11.83 25.22 25.49
17.63 13.86 15.41 36.44 10.03
2.73 4.22 17.16 9.96 74.12
29.11 5.44 6.09 56.26 9.85
20.29 9.48 12.97 82.23 26.73
3.99 4.64 9.35 13.04 50.19
22.65 11.13 14.3 50.51 21.59
4.43 7.3 14.36 29.04 44.74
5.4 8.9 12.53 65.5 23.27
7.06 2.79 5.24 19.79 40.68
19.82 10.53 18.55 42.04 37.19
7.26 2.99 6.99 22.72 56.58];
n = size(ssgs, 1);
x = ssgs(:, [1:4]);
y = ssgs(:, 5);
x = zscore(x); % 对前四个收益指标标准化处理

r = corrcoef(x); % 计算相关系数矩阵(皮尔逊系数)
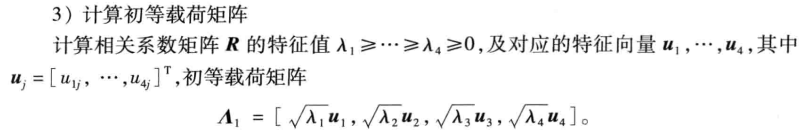
[vec1, val, con1] = pcacov(r)
f1 = repmat(sign(sum(vec1)), size(vec1, 1), 1);
vec2 = vec1.*f1; % mu
f2 = repmat(sqrt(val)', size(vec2, 1), 1); % 根号lamda
a = vec2 .* f2 % 根号lamda * mu 初等载荷矩阵
这里<=4因为总共就4个

num = input('请选择主因子个数'); % 选择主因子个数
am = a(:, [1:num]); % 提出num个主因子的载荷矩阵
[bm, t] = rotatefactors(am, 'method', 'varimax') %am旋转变换,bm为旋转后的载荷阵
bt = [bm, a(:, [num+1:end])]; % 旋转后全部因子的载荷矩阵,前两个旋转,后面不旋转
con2 = sum(bt.^2) % 计算因子贡献
check = [con1, con2'/sum(con2) * 100] % 该语句是领会旋转意义,con1是未旋转前的贡献率
rate = con2(1:num)/sum(con2) % 计算因子贡献率


coef = inv(r) * bm % 计算得分函数的系数
score = x * coef % 计算各个因子的得分
weight = rate/sum(rate) % 计算得分的权重
Tscore = score * weight' % 对各个因子的得分进行加权求和,即求各企业的综合得分
[STscore, ind] = sort(Tscore, 'descend') % 对企业进行排序
display = [score(ind, :)'; STscore'; ind'] % 显示排序结果
[ccoef, p] = corrcoef([Tscore, y]) % 计算F与资产负债的相关性系数
[d, dt, e, et, stats] = regress(Tscore, [ones(n, 1), y]); % 计算F与资产负债的方程
d, stats % 显示回归系数,和相关统计量的值
完整代码如下:
clc,clear
ssgs = [43.31 7.39 8.73 54.89 15.35
17.11 12.13 17.29 44.25 29.69
21.11 6.03 7 89.37 13.82
29.55 8.62 10.13 73 14.88
11 8.41 11.83 25.22 25.49
17.63 13.86 15.41 36.44 10.03
2.73 4.22 17.16 9.96 74.12
29.11 5.44 6.09 56.26 9.85
20.29 9.48 12.97 82.23 26.73
3.99 4.64 9.35 13.04 50.19
22.65 11.13 14.3 50.51 21.59
4.43 7.3 14.36 29.04 44.74
5.4 8.9 12.53 65.5 23.27
7.06 2.79 5.24 19.79 40.68
19.82 10.53 18.55 42.04 37.19
7.26 2.99 6.99 22.72 56.58];
n = size(ssgs, 1);
x = ssgs(:, [1:4]);
KMO(x)
y = ssgs(:, 5);
x = zscore(x);% 对前四个收益指标标准化处理
r = corrcoef(x); % 求相关系数矩阵
[vec1, val, con1] = pcacov(r); % 进行主成分分析的相关计算
f1 = repmat(sign(sum(vec1)), size(vec1, 1), 1);
vec2 = vec1.*f1; % 特征向量正负号转换
f2 = repmat(sqrt(val)', size(vec2, 1), 1);
a = vec2 .* f2 % 求初等载荷矩阵
num = input('请选择主因子个数'); % 选择主因子个数
am = a(:, [1:num]); % 提出num个主因子的载荷矩阵
[bm, t] = rotatefactors(am, 'method', 'varimax') %am旋转变换,bm为旋转后的载荷阵
bt = [bm, a(:, [num+1:end])]; % 旋转后全部因子的载荷矩阵,前两个旋转,后面不旋转
con2 = sum(bt.^2) % 计算因子贡献
check = [con1, con2'/sum(con2) * 100] % 该语句是领会旋转意义,con1是未旋转前的贡献率
rate = con2(1:num)/sum(con2) % 计算因子贡献率
coef = inv(r) * bm % 计算得分函数的系数
score = x * coef % 计算各个因子的得分
weight = rate/sum(rate) % 计算得分的权重
Tscore = score * weight' % 对各个因子的得分进行加权求和,即求各企业的综合得分
[STscore, ind] = sort(Tscore, 'descend') % 对企业进行排序
display = [score(ind, :)'; STscore'; ind']; % 显示排序结果
[ccoef, p] = corrcoef([Tscore, y]) % 计算F与资产负债的相关性系数
[d, dt, e, et, stats] = regress(Tscore, [ones(n, 1), y]); % 计算F与资产负债的方程
d, stats % 显示回归系数,和相关统计量的值
KMO函数的代码(评价里也不知道要不要进行检验,先放着好了)
function kmo=KMO(x)
R=corrcoef(x); % 简单相关系数
P=partialcorr(x); %偏相关系数
R_1=R-eye(size(R)); %简单相关系数减去对角线上的1
P_1=P-eye(size(P)); %偏相关系数减去对角线上的1
KMO=sum(R_1(:).^2)/(sum(R_1(:).^2)+sum(P_1(:).^2))
end