一、题目[LeetCode-108]

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵 高度平衡?二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例 1：

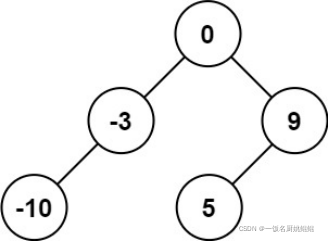
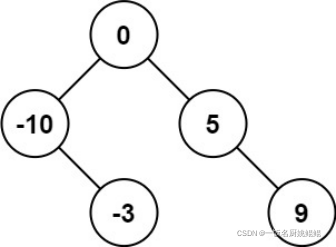
输入：nums = [-10,-3,0,5,9]

输出：[0,-3,9,-10,null,5]

解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

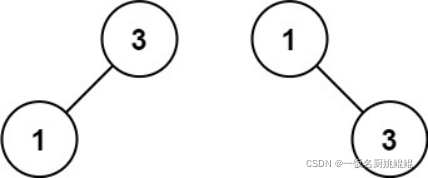
输入：nums = [1,3]

输出：[3,1]

解释：[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

?

提示：

1 <= nums.length <= 10^4
-10^4?<= nums[i] <= 10^4
nums?按?严格递增?顺序排列

二、思路

递归：中序遍历转为层次遍历

1)首先处理数组nums，将其严格递增的排列顺序更改为最终所求平衡BST树的层次遍历顺序（即根值为nums[0]，根的左儿子的值为nums[1]，根的右儿子的值为nums[2]，根的左儿子的左儿子的值为nums[3]）。

这里使用递归的方法。先找出数组nums的中间数nums[nums.size()/2]（该数将作为生成的数的根节点），将其赋值给新数组的第一位newNums[0]，然后递归处理子区间nums[0, middle - 1]和nums[middle + 1, nums.size()-1]，找出的中位数分别作为newNums[1], newNums[2]。

具体流程：首先创建一个新数组newNum，大小拓展为刚好超过num.size()的2^i-1（这样是最近的完全二叉树的个数），多出来的位置便是二叉树的nullptr，这样有利于后续递归子函数调用的统一化。然后编写递归子函数，其中有一个参数index，意为插入到newNum中的位置。它的递归方式为：对于当前节点在newNum中的位置为index，则左儿子的位置为2index+1，右儿子位置为2index+2。

2)将nums转化为二叉搜索树。这里再次使用递归的方法。对于任意节点nums[i]，其左右子节点值分别为nums[2i+1]，nums[2i+2]（在不越界的情况下）。利用这个性质我们便可进行递归构造二叉搜索树。

/**
?*?Definition?for?a?binary?tree?node.
?*?struct?TreeNode?{
?*?????int?val;
?*?????TreeNode?*left;
?*?????TreeNode?*right;
?*?????TreeNode()?:?val(0),?left(nullptr),?right(nullptr)?{}
?*?????TreeNode(int?x)?:?val(x),?left(nullptr),?right(nullptr)?{}
?*?????TreeNode(int?x,?TreeNode?*left,?TreeNode?*right)?:?val(x),?left(left),?right(right)?{}
?*?};
?*/
class?Solution?{
public:
????const?int?INTOFNULL?=?10001;
????TreeNode*?sortedArrayToBST(vector<int>&?nums)?{
????????vector<int>?newNums?=?moveArray(nums);
????????return?creatTreeNodes(newNums,?0);
????}
????vector<int>?moveArray(vector<int>&?nums){//创建新数组newNum，里面是将nums的元素由递增排序变为层次遍历的排序。（大小拓展到恰好大于nums.size()的完全二叉树大小，多出来的位置即是nullptr）并在这里调用重载递归子函数。
????????int?n?=?nums.size();
????????int?i?=?1;
????????while(pow(2,i)-1?<?n)
????????????i++;
????????vector<int>?newNums(pow(2,i)-1);//找出离n最近的恰好大于n的完全二叉树的节点个数，作为新数组的size
????????moveArray(nums,?newNums,?0,?nums.size()-1,?0);//重载递归子函数
????????return?newNums;
????}
????void?moveArray(vector<int>&?nums,?vector<int>&?newNums,?int?left,?int?right,?int?index){
????????if(index?>=?newNums.size())//递归基————如果index越界了直接返回
????????????return;
????????if(left?>?right)//当左边界大于右边界时，调用它的上一个函数是middle==left或middle==right，到这里是空节点了
????????{
????????????newNums[index]?=?INTOFNULL;//表明newNums的该位置在二叉树中是nullptr
????????????return;
????????}
????????int?middle?=?(left?+?right)/2;
????????newNums[index]?=?nums[middle];//将中间值插入新数组的对应位置index
????????moveArray(nums,?newNums,?left,?middle-1,?index*2+1);//递归调用。这里左儿子的index便是2index+1
????????moveArray(nums,?newNums,?middle+1,?right,?index*2+2);//递归调用。这里右儿子的index便是2index+2
????}
????TreeNode*?creatTreeNodes(vector<int>&?nums,?int?index){
????????if(index?>=?nums.size()?||?nums[index]?==?INTOFNULL)
????????????return?nullptr;
????????return?new?TreeNode(nums[index],?creatTreeNodes(nums,?index*2+1),?creatTreeNodes(nums,?index*2+2));
????}
};

三、官方题解（来源：力扣（LeetCode））?

方法一：中序遍历，总是选择中间位置左边的数字作为根节点

选择中间位置左边的数字作为根节点，则根节点的下标为 mid=(left+right)/2，此处的除法为整数除法。

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-33/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。

方法二：中序遍历，总是选择中间位置右边的数字作为根节点

选择中间位置右边的数字作为根节点，则根节点的下标为 mid=(left+right+1)/2，此处的除法为整数除法。

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置右边的数字作为根节点
        int mid = (left + right + 1) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-33/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。

方法三：中序遍历，选择任意一个中间位置数字作为根节点

选择任意一个中间位置数字作为根节点，则根节点的下标为 mid=(left+right)/2 和 mid=(left+right+1)/2 两者中随机选择一个，此处的除法为整数除法。

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 选择任意一个中间位置数字作为根节点
        int mid = (left + right + rand() % 2) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-33/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复杂度分析

时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
空间复杂度：O(logn)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(logn)。

四、学习心得

①二叉搜索树BST的中序遍历结果即为一个严格递增的数组

因此本题其实给的即是所求二叉搜索树的中序遍历结果。对于一个二叉树的中序遍历结果：

中序遍历结果不能唯一地确定二叉搜索树
中序遍历结果不能唯一地确定平衡二叉搜索树，但是对于每一棵子树的创建时，根从中序数组区间中的选取位置各有最多两种选择（对于子树的节点个数（中序遍历数组对应的区间长度）为奇数时，根只有一个选择——数组区间中间值；为偶数时，根有两种选择——中间位置的左边值和中间位置的右边值）

因此，官方解法中，一种思路给出了三种可供选择的根选取的方法。

②数组越界问题

在递归地选定数组区间（涉及到参数left和right）时，递归基为left恰好比right大于1，这时应当在递归子函数的前面先用if语句写出对应的特殊操作——返回null指针，否则将会越界。