题目概述

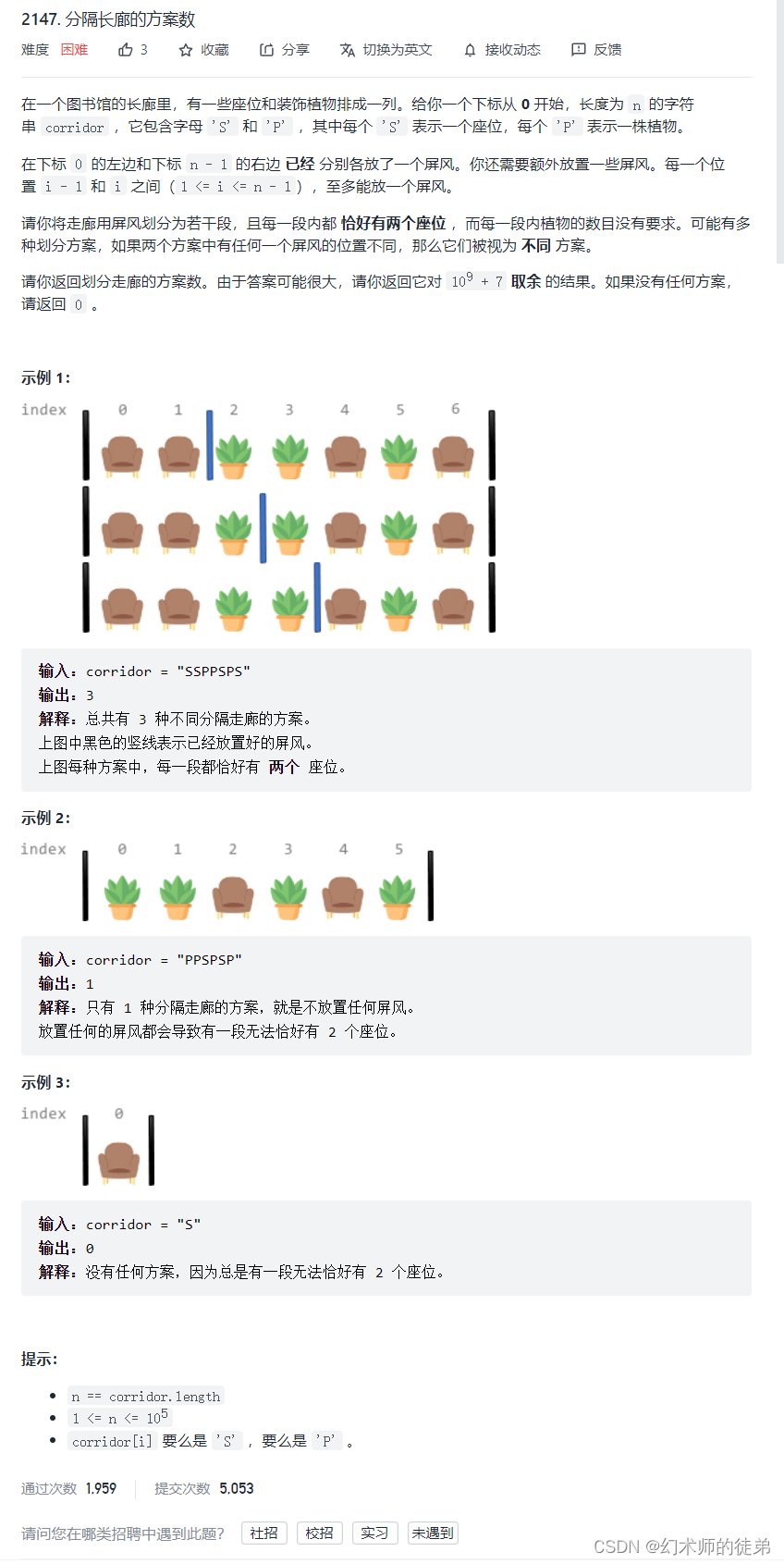
在这里插入图片描述

题解

??这个题需要多看图，仔细看图会发现你只能在第 $2 i$ 个椅子和第 $2 i + 1$ 个椅子之间摆放屏风( $i = 1, 2, 3, . . .$ ),其他位置都不能摆放屏风，因为其他位置在上一个屏风到这个位置之前的椅子数不够2个。
??那既然只能在第 $2 i$ 个椅子和第 $2 i + 1$ 个椅子之间摆放屏风，那么两个位置之间摆放屏风的方法数就是第 $2 i + 1$ 个椅子的下标和第 $2 i$ 个椅子的下标之差，然后根据乘法原理，把这些第2个椅子和第3个椅子之间摆放屏风的方法数、第4个椅子和第5个椅子之间摆放屏风的方法数…乘起来就可以了。
??另外，本题要注意边界条件：如果椅子的个数是奇数个，那么不可能通过摆放屏风分成每块都有两个椅子的块，所以如果椅子个数是奇数个，直接返回0；另外，如果压根没有椅子，那何谈摆放屏风的方法，也返回0.
??下面提供两种实现思路的代码，一种比较蠢，是我理解了大佬的思路后自己实现的，具体就是用一个数组记录每个椅子的下标，然后挑数组中第3个元素和第2个元素作差与返回结果累乘、数组中第5个元素和第4个元素累乘…因为数据比较大记得取模。

class Solution {
public:
    int numberOfWays(string corridor) 
    {
        /*
        遍历一遍数组 如果座位的个数是奇数 那么无解 返回0
        如果座位数目是偶数，那么我们只能在第2i个座位和第2i+1个座位之间摆放屏风
        记录座位的下标 这两个座位之间摆放屏风的方法数等于座位下标之差
        最后把每个方法数乘起来就是结果
        */
        int mod = 1e9 + 7;
        vector<int> chairlocation;
        int size = corridor.size();
        for (int i = 0; i < size; ++i)
        {
            if (corridor[i] == 'S')
            {
                chairlocation.push_back(i);
            }
        }
        int chairnum = chairlocation.size();
        if (chairnum == 0)
        {
            return 0;
        }
        if (chairnum % 2 != 0)
        {
            return 0;
        }
        long long ret = 1;
        for (int i = 1; 2 * i <= chairnum; ++i)
        {
            if (2 * i + 1 < chairnum)
            {
                long long ways = chairlocation[2 * i + 1 - 1] - chairlocation[2 * i - 1];
                ret = (ret * ways) % mod;
            }
        }
        return ret % mod;
    }
};

??这个思路完全没必要实现的这么麻烦，由于只需要奇数的前继，只要遍历时一直更新前继椅子的下标就好了。

class Solution {
public:
    int numberOfWays(string corridor) 
    {
        /*
        化简之前的思路 为了得到第2i个椅子和第2i+1个椅子的下标
        其实没有必要记录每个椅子的下标
        只要当前椅子是第3个、第5个、第7个、第9个椅子的时候
        就可以通过当前椅子的下标减去前一个椅子的下标值得到一次可摆放的屏风数
        累乘起来就可以了
        所以我只要有一个prev记录前一个椅子的下标
        一个chaircnt记录椅子的个数
        如果chaircnt%2 == 1且当前椅子个数>=3时
        就可以计算一次屏风摆放方法数 = i - prev 然后累成就可以
        */    
        int mod = 1e9 + 7;
        int chairnum = 0;
        int size = corridor.size();
        int ret = 1;
        int prev = 0;
        for (int i = 0; i < size; ++i)
        {
            if (corridor[i] == 'S')
            {
                ++chairnum;
                if (chairnum >= 3 && chairnum % 2 == 1)
                {
                    ret = (long)ret * (i - prev) % mod;
                }
                prev = i;
            }
        }
        return chairnum == 0? 0 : (chairnum % 2 == 0 ? ret : 0);
    }
};