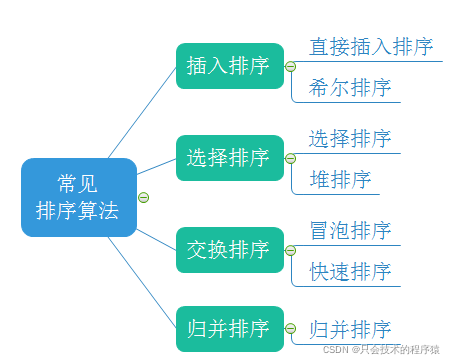
【目录】
1.插入排序
2.希尔排序
3.选择排序
4.堆排序
5.冒泡排序
6.快速排序
7.归并排序
本节目标;
:分析常见的比较排序算法基本原理及实现
:分析排序算法的性能分析
:分析Java中常用排序方法
1 排序
? ? ? ?排序,就是使一串记录,按照其中某个或某些关键字的大小,递增或递减排列的操作。
平时的上下文中,提到排序 通常指排升序。
2 稳定性
? ? ?两个相同的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则称该算法具备稳定发行。
【插入排序】
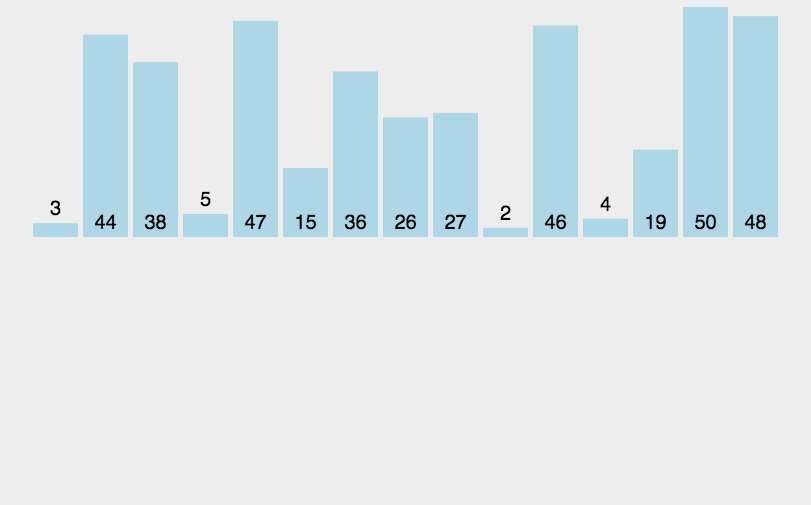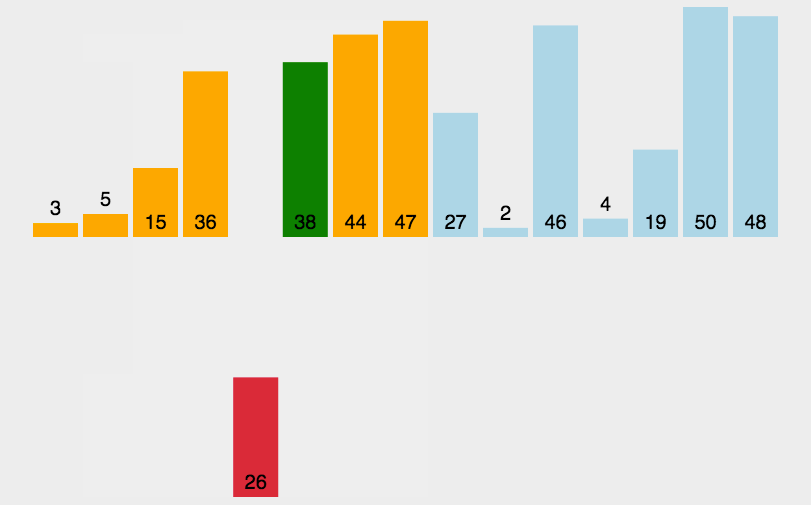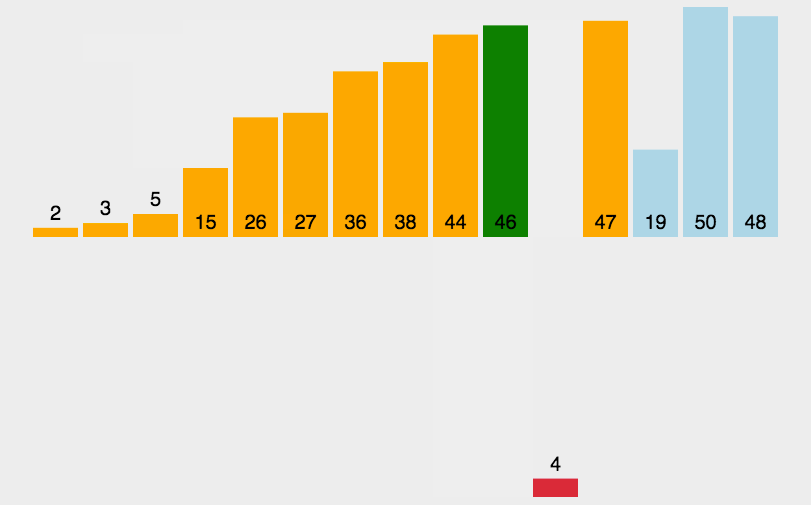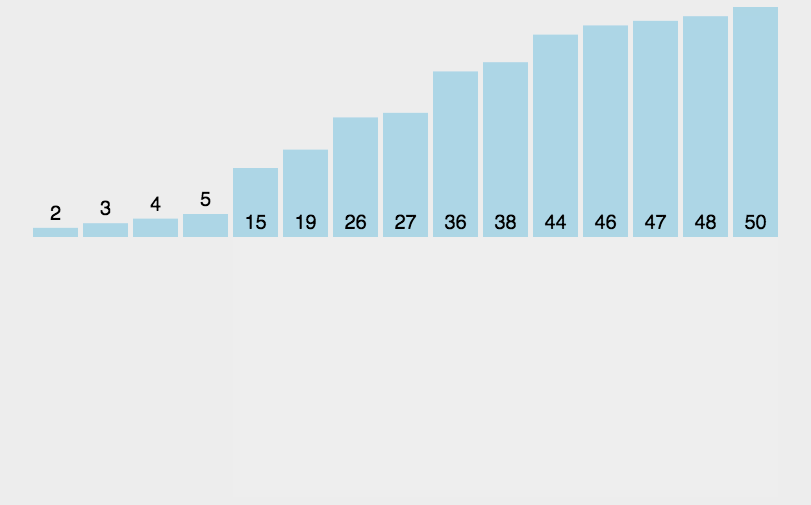
??【优化版】
? 分析步骤;
第一步;将第一个元素下标设置为 i?,设 index? 与 i 指向同一个元素
第二部 设置循环 利用 j? 循环找出除 第一个元素以为最小的元素 将其交到index下
第三步 将index 与 第一个元素交换
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0 ; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}else {
//array[j+1] = tmp; 只要j回退的时候,遇到了 比tmp小的元素就结束这次的比较
break;
}
}
//j回退到了 小于0 的地方
array[j+1] = tmp;
}
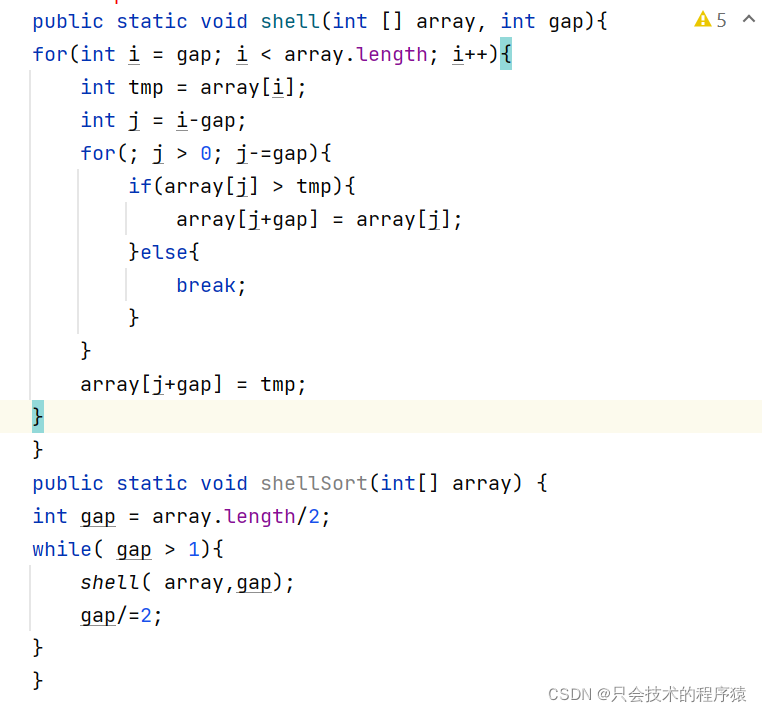
}【希尔排序】(以了解为主 面试很少考的)
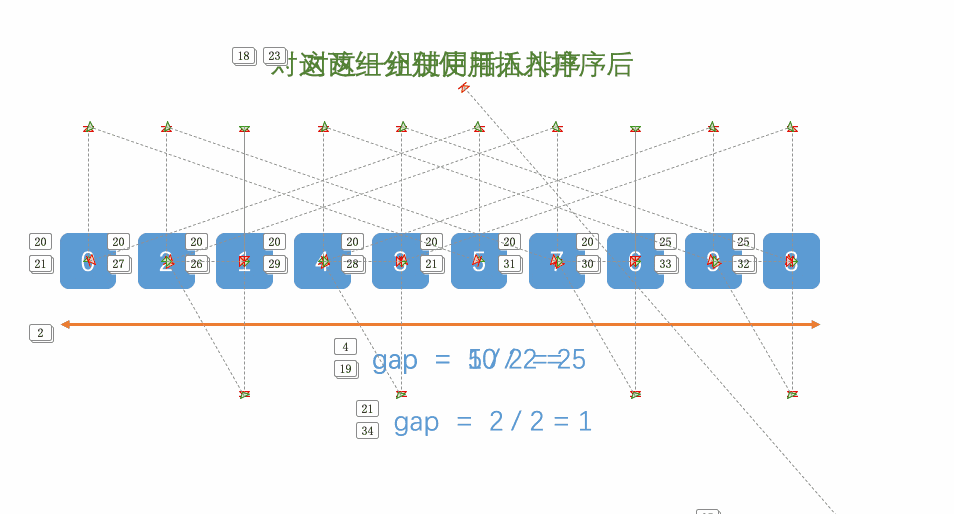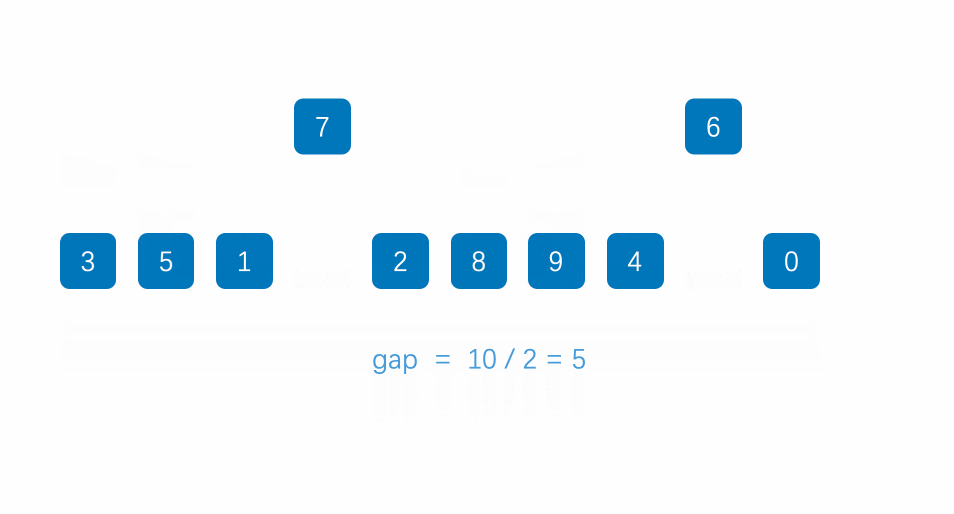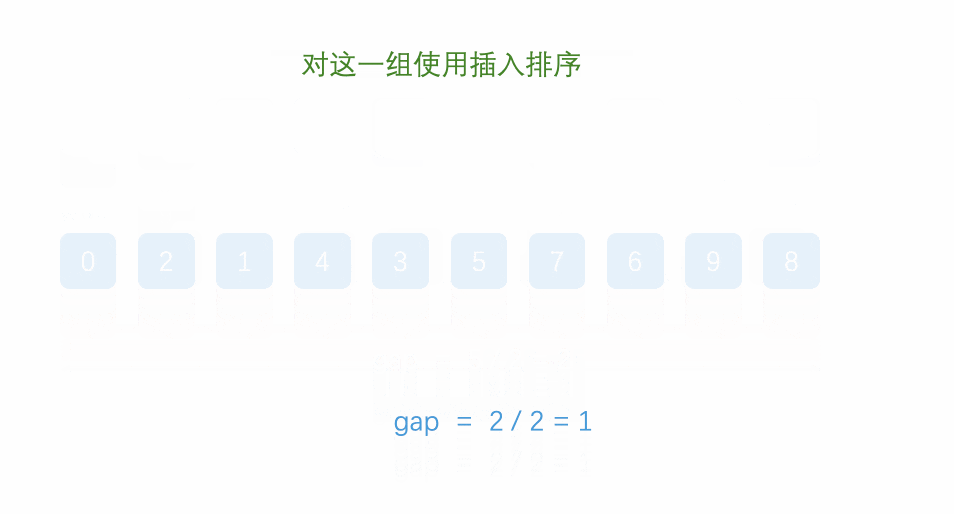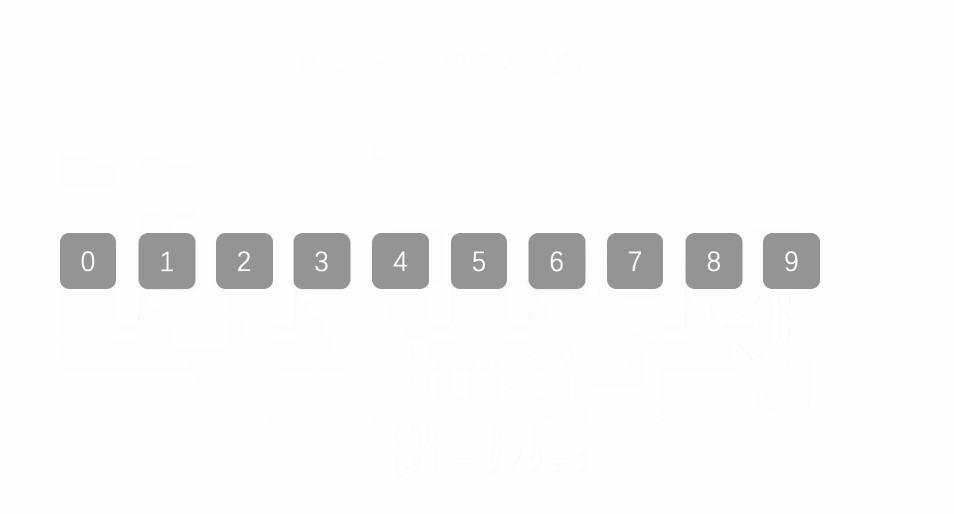
【分析步骤 】
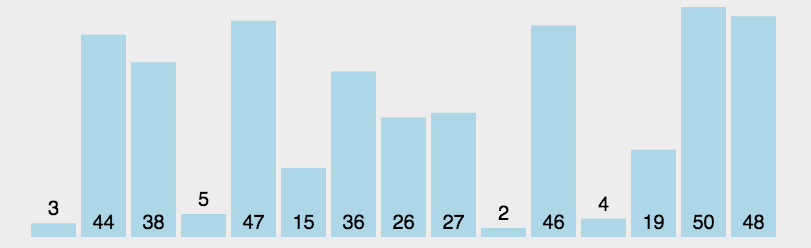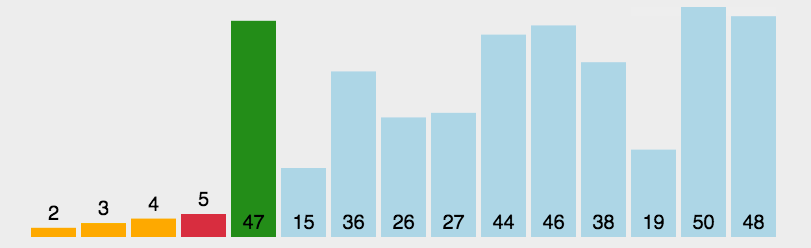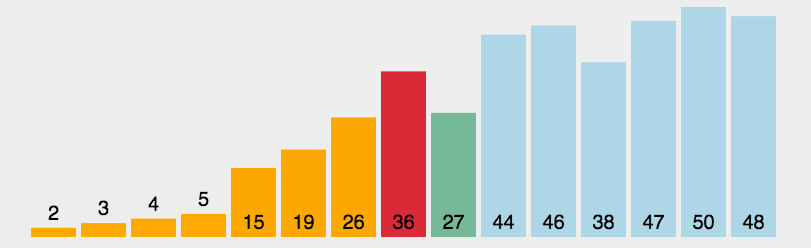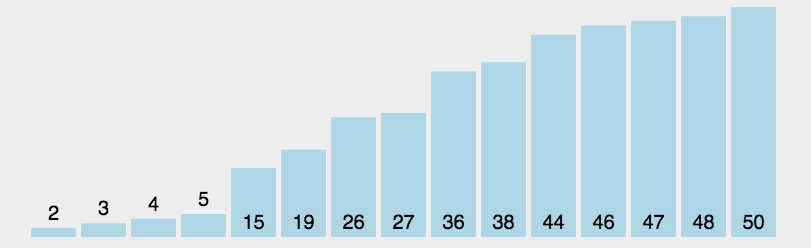
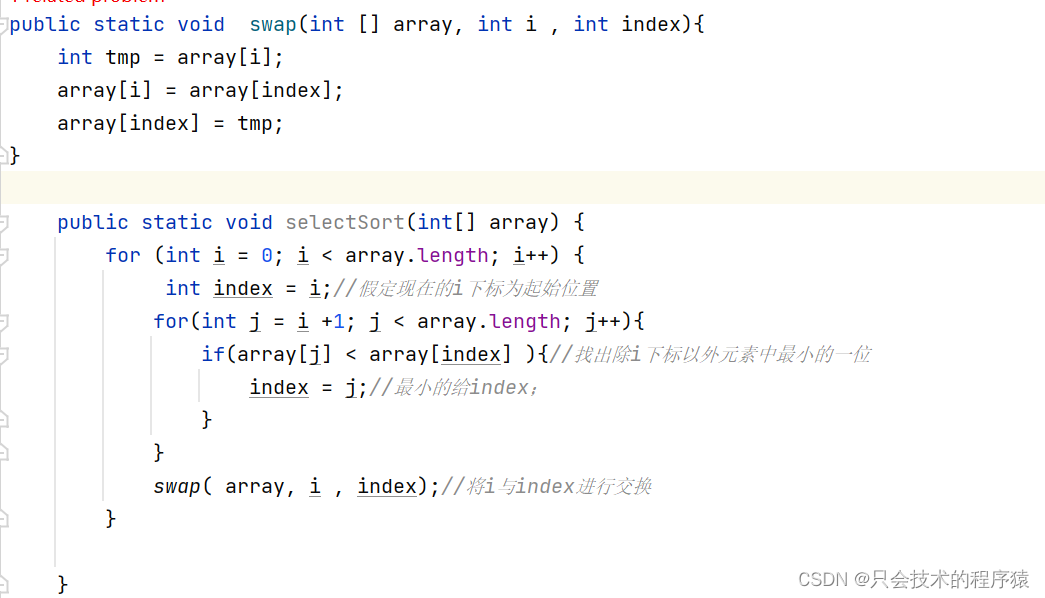
【选择排序】
? 分析步骤;
第一步;将第一个元素下标设置为 i?,设 index? 与 i 指向同一个元素
第二部 设置循环 利用 j? 循环找出除 第一个元素以为最小的元素 将其交到index下
第三步 将index 与 第一个元素交换
?
【堆排序】?
注释 !其基本原理还是排序.只其用堆来进行无序间排序,不用遍历进行排序
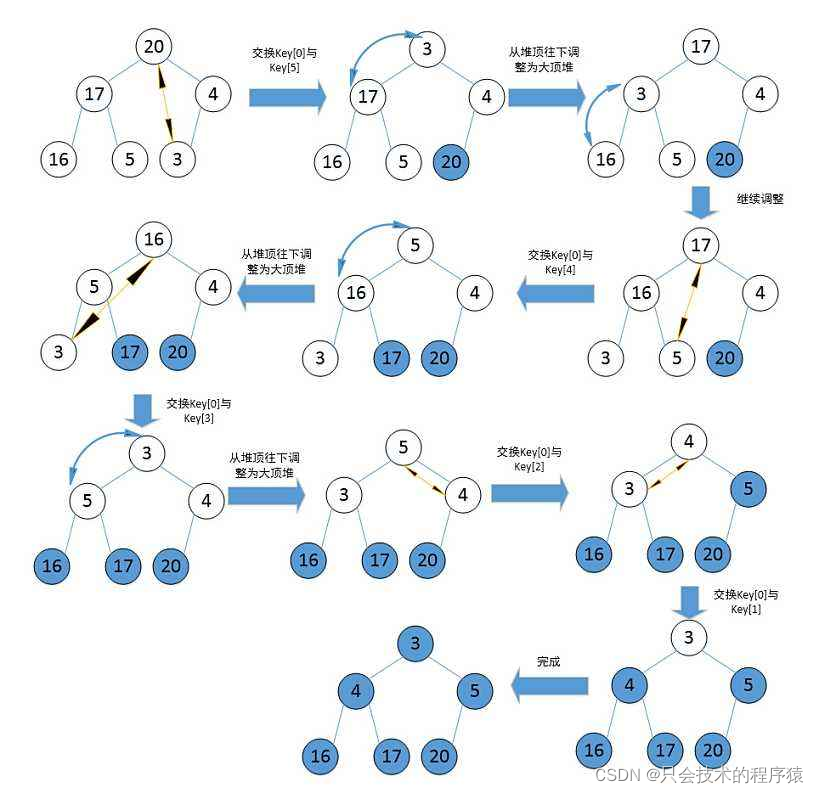
?
public static void createHeap(int[] array) {
for (int parent = (array.length - 1 - 1) / 2; parent > 0; parent--) {//设置出父亲节点
shiftDown(array, parent, array.length);//
}
}
public static void shiftDown(int[] array, int parent, int len) {
int child = 2 * parent + 1;//设置出子节点
while (child < len) {
if (child + 1 < len && array[child] < array[child + 1]) {
child++;//以防有两个子节点 找出两个子节点最大一位
}
if (array[child] > array[parent]) {
swap(array, parent, child);//交换父亲节点和子节点
parent = child;//从新设置父亲节点
child = 2*parent+1;
}else{
break;
}
}
}
public static void heapSort(int[] array) {//
createHeap( array);
int end = array.length-1;//每次交换完最后一位元素减一位
while(end > 0){
swap(array,0,end);
shiftDown(array,0, array.length-1);//这个循环里 向下转型
end--;
}
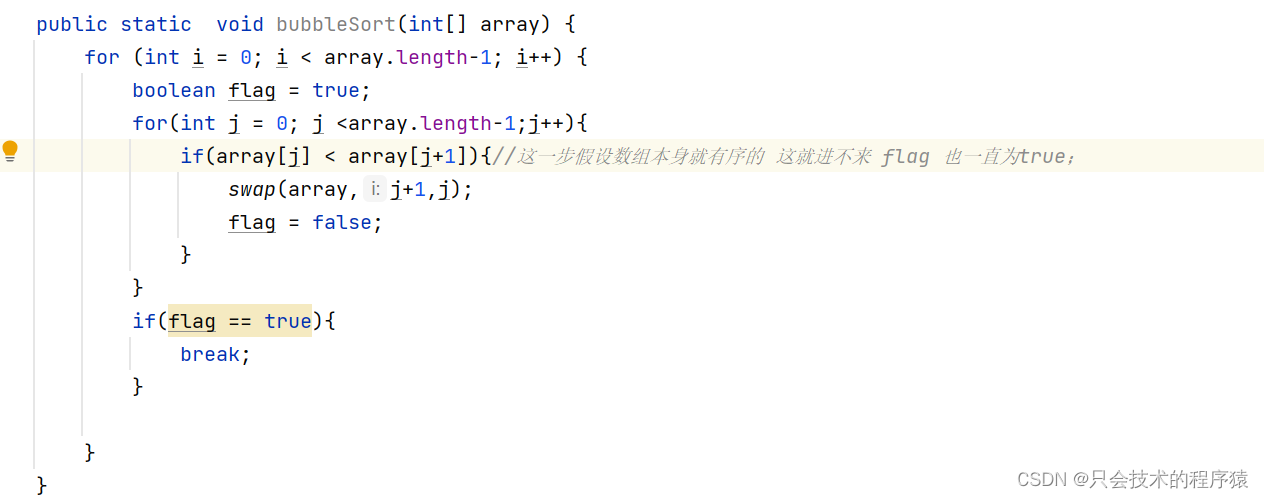
}【冒泡排序】
注释;可能是几种排序比较简单的一种
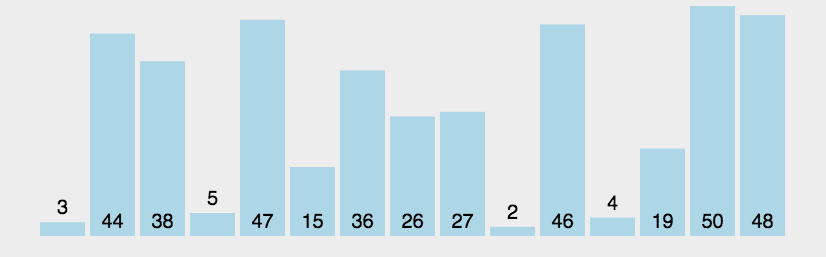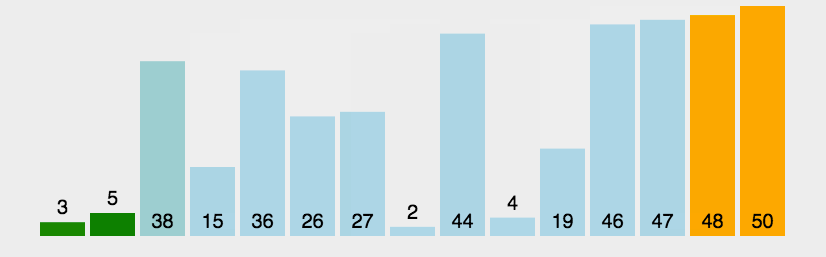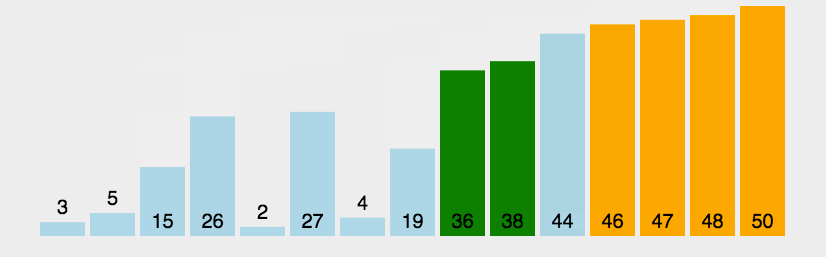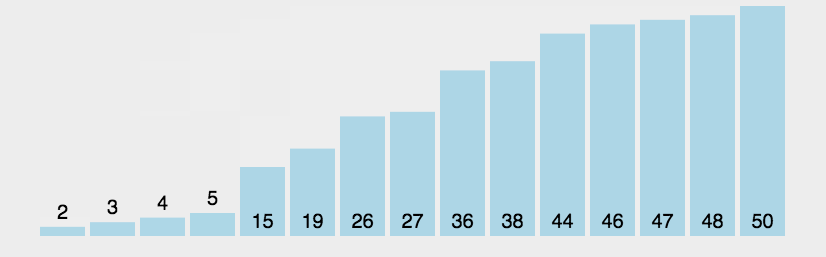
?
介绍一个冒泡排序的优化方法;?
【快速排序】
原理简介-总览
? ? 1? ?从待排序区间选择一个数,作为基准值(pivot)
? ? 2? ?partition:遍历整个待排序区间, 将比基准小的(可以与基准相同)放在基左侧,将比基准大? ? ? ? ? ? ? ? ? ?的(可以与基准相同)放在基准右侧。
? ??3? ?采用分治思想,对左右两个小区间按照同样的方法进行处理? 直到小区间的长度 == 1; 则其? ? ? ? ? ? ? ? ?代表有序,如果长度 ==0, 则代表没有元素。
??
? ? ? ? ? ? ? ? ? ? ? ? ? 
public static void quick(int[] array,int left,int right) {
if( left >= right) {//判断递归条件 不满足退出
return;
}
int pivot = partition( array,left,right);//找出基准值
quick( array, left, pivot-1);//左侧进行递归
quick( array, pivot+1 ,right);//右侧进行递归
}
private static int partition(int[] array,int start,int end) {
int tmp = array[start];
while(start< end){//
while(start< end &&array[end] > tmp){//末尾值比tmp大时 将末尾下标减减
end--;
}
array[start] = array[end];//在右侧遇到比tmp小的元素 进行交换
while(start< end && array[start] < tmp ){//先从头部进行比较 比tmp小时交换
start++;
}
array[end] = array[start];
}
array[end] = tmp;
return end;
}
public static void quickSort(int[] array) {
quick(array,0, array.length-1);
}
}
}【归并排序】
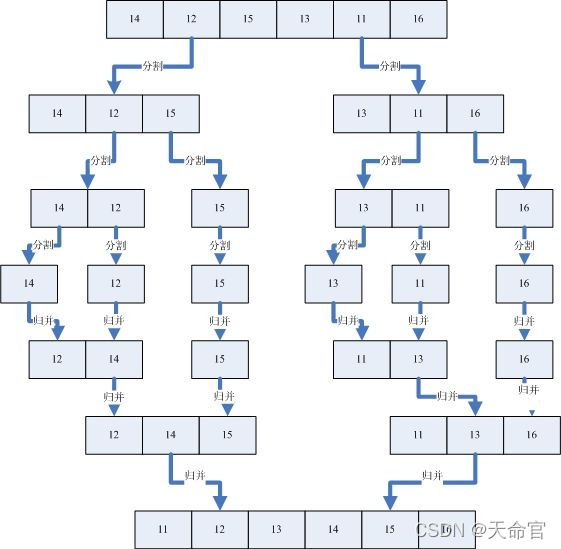
原理-总览
? ? ? 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法采用分治法(Divide and Conquer)的一个非常典型的应用。将以有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
在此之前先复习一下(链表题)【合并两个有序链表】(归并排序的基础)
public static int[] mergeArray(int[] array1,int[] array2) {
//注意判断参数
int [] tmp = new int[array1.length + array2.length];
int i = 0;
int s1 = 0;
int e1 = array1.length-1;
int s2 = 0;
int e2 = array2.length-1;
while( s1<e1 && s2<e2){
if(array1[s1] < array2[s2]){
tmp[i++] = array1[s1++];
}
if(array1[s1] > array2[s2]){
tmp[i++] = array2[s2++];
}
}
while( s1<= e1){
tmp[i++] = array1[s1++];
}
while( s2<= e2){
tmp[i++] = array2[s2++];
}
return tmp;【正文】
?
?
【代码简介;】?
public static void mergeSort1(int[] array) {
mergeSortInternal(array,0,array.length-1) ;
}
private static void mergeSortInternal(int[] array,int low,int high) {
if(low > high){
return ;
}
int mid = (low +(high-low))/2;//找到数组的中间位置 分为左右两部分
mergeSortInternal( array, low,mid-1 );// 将左边部分进行递归排序
mergeSortInternal( array, mid+1,high );// 将右边部分进行递归排序
merge(array,low,mid,high);// 将两部分进行合并
}
private static void merge(int[] array,int low,int mid,int high) {
int [] tmp = new int[array.length];//创建一个新的数组
int s1 = low;
int e1 = mid;
int s2 = mid+1;
int e2 = high;
int i = 0;
while(s1<e1 && s2<e2){//循环的的条件
if(array[s1] < array[s2]){
tmp[i++] = array[s1++];
}else{
tmp[i++] = array[s2++];
}
}
while(s1 < s2){//当到这一步 说明左侧比右侧长 将左侧剩余部分衔接到数组中
tmp[i++] = array[s1++];
}
while(s2 < e2){
tmp[i++] = array[s2++];//当到这一步 说明左侧比右侧长 将左侧剩余部分衔接到数组中
}
for(int j = 0; j < i; j++){//将tmp数组中元素放置array数组中
array[i+low] = tmp[j];
}
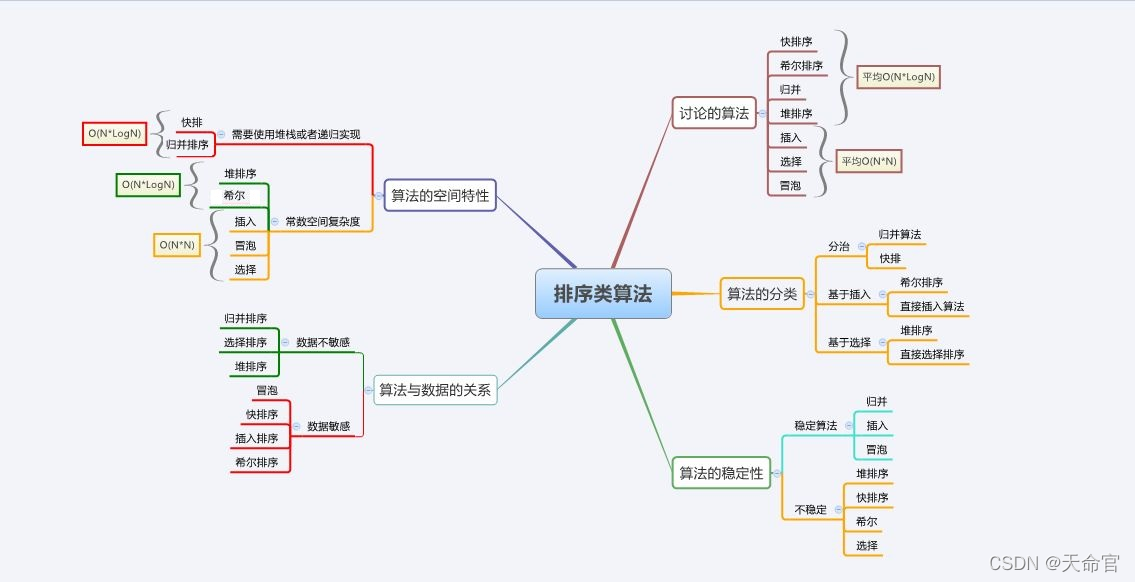
【排序总结】
? ? ??
?
| 排序方法 | 最好 | ? 平均 | 最坏 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | ?O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n*log(n)) | O(n*log(n)) | O(n*log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n*log(n)) | O(n*log(n)) | O(n^2) | O(log(n))~O(n) | 不稳定 |
| 归并排序 | O(n*log(n)) | O(n*log(n)) | O(n*log(n)) | O(n) | 稳定 |