Hash 表又称为散列表,一般由 Hash 函数(散列函数)与链表结构共同实现。与离散化思想类似,当我们要对若干复杂信息进行统计时,可以用 Hash 函数把这些复杂信息映射到一个容易维护的值域内。因为值域变简单、范围变小有可能造成两个不同的原始信息被 Hash 函数映射为相同的值所有我们需要处理这种冲突情况。
拉链法
思想
有一种称为“开散列”的解决方案是,建立个邻接表结构,以 Hash 函数的值域作为表头数组 head ,映射后的值相同的原始信息被分到同一类构成一个链表接在对应的表头之后,链表的节点上可以保存原始信息和一些统计数据。
Hash 表主要包括来两个基本操作:
- 1.计算 Hash 函数的值。
- 2.定位到对应链表中依次遍历、比较。
无论是检查任意一个给定的原始信息在 Hash 表中是否存在,还是更新它在 Hash 表中的统计数据都需要基这两个基本操作进行。
当 Hash 函数设计较好时,原始信息会被比较均匀地分配到各个表头之后从而使每次查找统计的时间降低到原始信息总数除以表头数组长度。若原始信息息数与表头数组长度都是 O ( N )级别且 Hash 函数分散均匀,几乎不产生冲突,那么每次查找,统计的时间复杂度期望为 O (1)。
例如,我们要在一个长度为 N 的随机整数序列 A 中统计每个数出现了多少次。当数列 A 中的值都比较小时,我们可以直接用一个数组计数(建立一个大小等于值域的数组进行统计和映射,其实就是最简单的 Hash 思想)。当数列 A 中的值很大时,我们可以把 A 排序后扫描统计。这里我们换一个思路,尝试一下 Hash 表的做法。设计 Hash 函数为 H ( x )=( x mod P )+1,其中 P 是一个比较大的质数但不超过 N 。显然这个 Hash 函数把数列 A 分成 P 类,我们可以依次考虑数列中的每个数 A[i],定位到 head [ H ( A [ i ])]这个表头所指向的链表。如果该链表中不包含A[i],我们就在表头后插入一个新节点 A[i],并在该节点上记录 A[i]出现了1次,否则我们就在直接找到已经存在的 A[i]节点将其出现次数+1。因为整数序列 A 是随机的,所以最终所有的 A[i]会比较均匀地分散在各个表头之后,整个算法的时间复杂度可以近似达到 O ( N )。
上面的例子是一个非常简单的 Hash 表的直观应用。对于非随机的数列,我们可以设计更好的 Hash 函数来保证其时间复杂度。同样的,如果我们需要维护的是比大整数复杂得多得信息的某些特性(如是否存在,出现次数等),也可以用 Hash 表来解决。
模板代码
int h[N], e[N], ne[N], idx;
//h数组里存的是指向链表的表头,初始值为-1
//e数组用来存链表结点的值
//ne存链表的下一个结点指针
//idx结点空间分配符
// 向哈希表中插入一个数
void insert(int x) //为什么要%了N后面还要+N,因为第一次取余可能有负数,但是数组下标不可能是负的,这么做是为了使结果为正数 c++中如果是负数 那他取模也是负的 所以 加N 再 %N 就一定是一个正数
{ //哈希函数:H(x)=(x % N + N) % N
int k = (x % N + N) % N; //映射的域的范围为【0,N)
e[idx] = x; //把新的结点插入到链表中
ne[idx] = h[k];
h[k] = idx ++ ; //idx++
}
// 在哈希表中查询某个数是否存在
bool find(int x)
{
int k = (x % N + N) % N; //通过哈希函数找到对应的值
for (int i = h[k]; i != -1; i = ne[i]) //去遍历值对应的链表
if (e[i] == x)
return true;
return false;
}
开放寻址法
思想
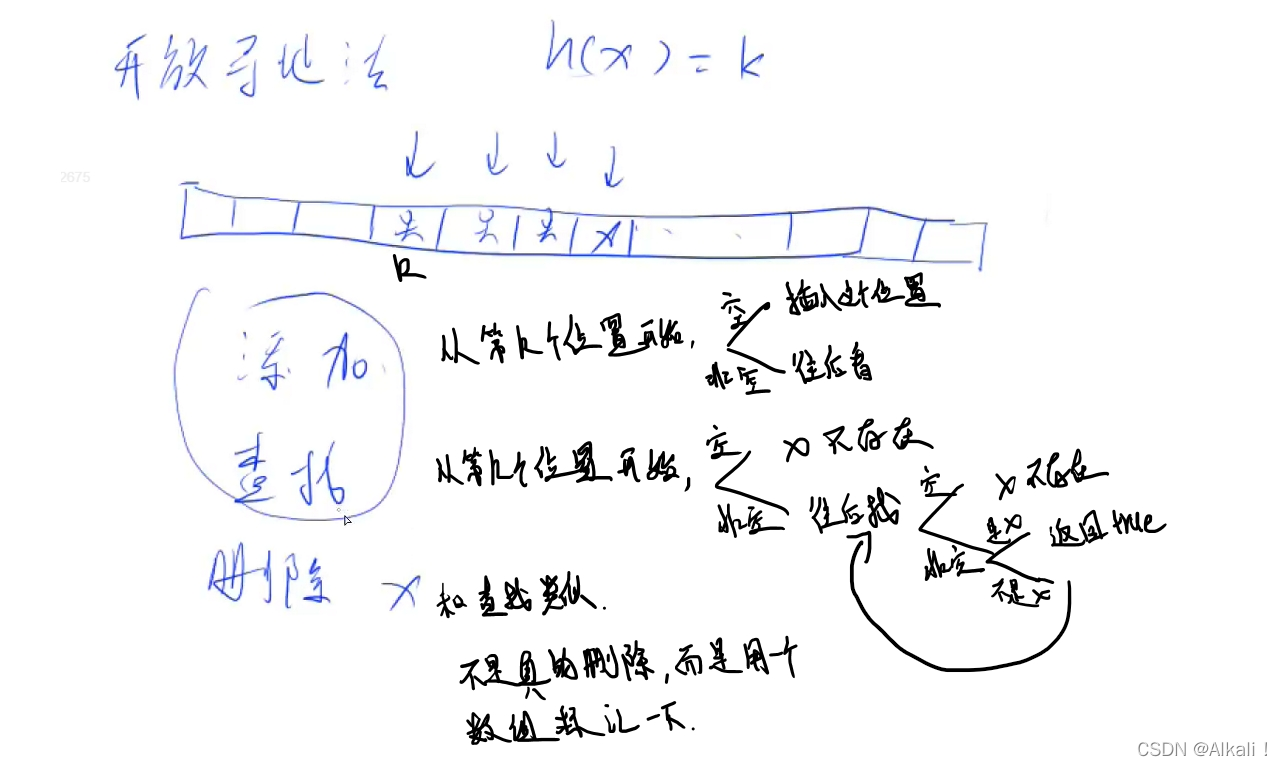
开放寻址法的冲突处理方式是:
- 当插入一个数x时,利用哈希函数找到位置k,判断位置k处是不是空的,如果是空的,那就把数放在这个地方;如果不是空的,就向后找,直到找到空位放下为止。
模板代码
int h[N];
// 如果x在哈希表中,返回x的下标;如果x不在哈希表中,返回x应该插入的位置
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x) //出来的条件,要么h[t] == null,要么h[t] == x,对应两种情况,前者x不在哈希表中,返回x应该插入的位置;后者x在哈希表中,返回x的下标
{
t ++ ;
if (t == N) t = 0; //如果找到数组末尾了,循环到数组头去查找
}
return t;
}
一般哈希中哈希函数中模数N的取值讲究
拉链法
一般取大于数据规模的第一个质数
开放寻址法
一般取数据规模的2~3倍往后的第一个质数,这样大概率就没有冲突了
(为什么相较于拉链法这么大?因为拉链法的冲突没占用数组,是立体的延申,开放寻址法就一个数组用来存储)