[数据结构与算法]复习算法基础（一）

/*呜呜呜我要逼自己打代码，不能再偷懒了呜呜呜*/

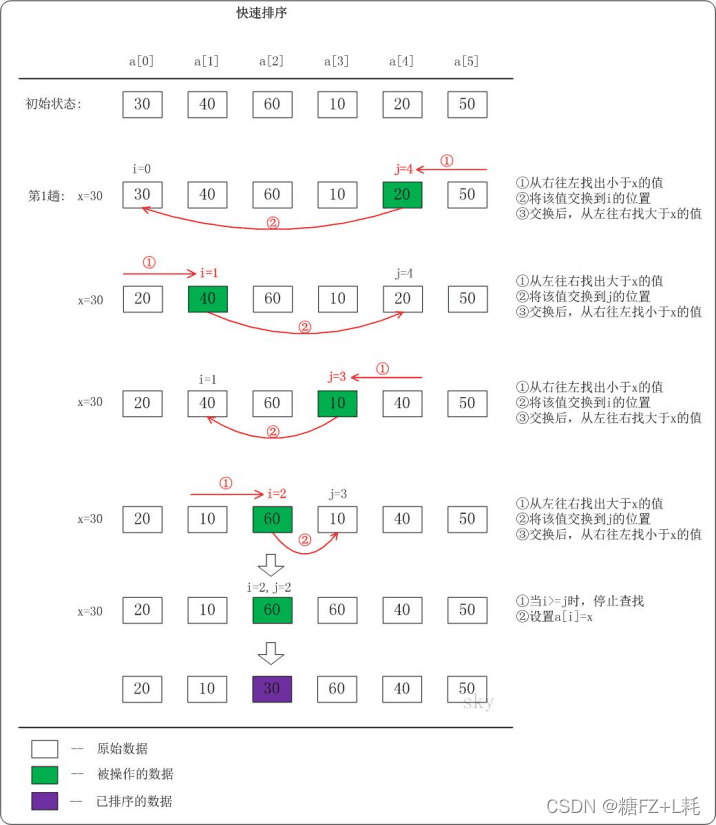
快速排序

快速排序时间复杂度
快速排序的时间复杂度在最坏情况下是O(N2)，平均的时间复杂度是O(N*lgN)。
这句话很好理解：假设被排序的数列中有N个数。遍历一次的时间复杂度是O(N)，需要遍历多少次呢？至少lg(N+1)次，最多N次。
(01) 为什么最少是lg(N+1)次？快速排序是采用的分治法进行遍历的，我们将它看作一棵二叉树，它需要遍历的次数就是二叉树的深度，而根据完全二叉树的定义，它的深度至少是lg(N+1)。因此，快速排序的遍历次数最少是lg(N+1)次。
(02) 为什么最多是N次？这个应该非常简单，还是将快速排序看作一棵二叉树，它的深度最大是N。因此，快读排序的遍历次数最多是N次。

coding：

#include <iostream>
using namespace std;

const int N = 100010;
int q[N], n;

void Swap(int &a, int &b)
{
    int temp = a;
    a = b;
    b = temp;
}

void Quick_sort(int left,int right)
{
    if (left >=right) return;
//    why subtract（减） one here？because subtract one is aim to  start //
//at the zero of the array index(数组索引)//（加一，又减一取二分一平均值的时候抵消）
    int i = left - 1, j = right + 1, val = q[left + right >> 1];
    while (i < j)
    {
        do i++; while (q[i] < val);//star at the left and comparing
        do j--; while (q[j] > val);//star at the right and comparing
        if (i < j)
        {
            Swap(q[i], q[j]);
        }
        Quick_sort(left, j);//Swap the values on the left
        Quick_sort(j + 1, right);//Swap the values on the right
    }
}

int main()
{
    cin >> n ;
    for (int i = 0; i < n; i++)  cin>> q[i];
    Quick_sort(0, n - 1);
    for (int i = 0; i < n; i++)    cout << q[i] << ' ';
    cout << endl;
    return 0;
}

模板题： 【模板】快速排序 - 洛谷

归并排序

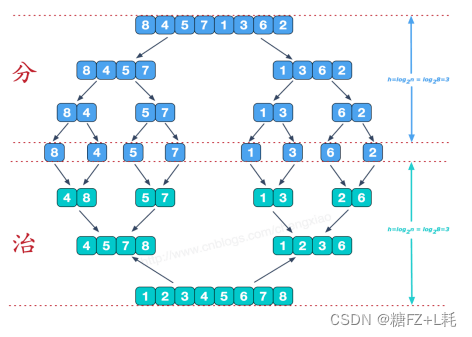
coding：

// Merge_sort学习.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include <iostream>
#include<cstring>
using namespace std;

const int N = 100010;
int q[N], n;
int temp[N];

void Merge_Sort(int l,int r)
{
    if (l >= r) return ;
    int mid = l + r >> 1;//divide by two
    Merge_Sort(l, mid), Merge_Sort(mid + 1, r);//sort left andthen right
    int i = l, j = mid + 1, k = l;
   //Divided into three cases
    while (i <= mid && j <= r)
    {
        if (q[i] < q[j]) temp[k++] = q[i++];
        else temp[k++] = q[j++];
    }//if left and the right both suit ,to do it
    while (i <= mid) temp[k++] = q[i++];//only left suits,so execuit the left 
    while (j <= r)    temp[k++] = q[j++];//only right suits,so execuit the right 
    //拷贝打印
    memcpy(q + l, temp + l, sizeof(int) * (r - l + 1));
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> q[i];
    Merge_Sort(0, n - 1);
    for (int i = 0; i < n; i++) cout<<q[i]<<' ';
    cout << endl;

    return 0;
}