[数据结构与算法]DS01 线性表实现

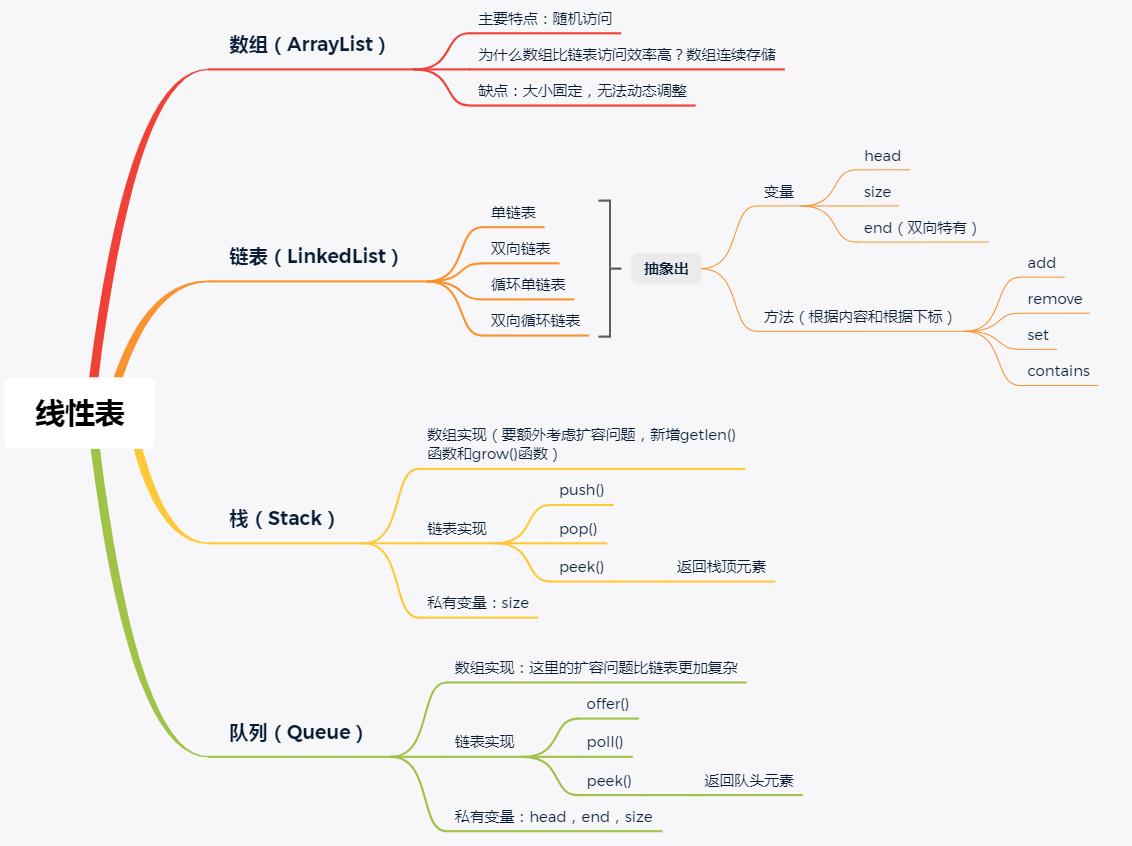
1, 数组

Q1: 数组我们都很熟悉，那你理解的数组是什么样的呢？它的最主要特点是什么呢？
    数组在内存空间上是连续存储 -> 随机访问
    
    某一个下标位置 = 数组的起始位置 + 下标 * 单个数组单元大小

Q2: 为什么数组的索引是一般都是从0开始的呢？ 历史遗留问题
    "易语言"  ->  数组下标从1开始
    
    如果从1开始:
    某一个下标位置 = 数组的起始位置 + (下标-1) * 单个数组单元大小
    
        
Q3: 为什么数组的效率比链表高？
    第一层: 
    数组在内存空间上是连续存储
    链表是非连续存储, 访问要一步一步next向后查找
    第二层:
    频繁的数据在缓存中置换, 比较消耗硬件开销

2, 链表

2.1链表的分类

链表是由结点构成的

// 单链表
 除了尾结点以外每个结点都有一个后继结点
// 循环单链表   
 在单链表的基础上, 让尾结点的下一个指向头结点 
// 双向链表
 是在单链表的基础上, 让每一个结点都有前后指向(除了头尾结点)     
// 双向循环链表  
 是在双向链表的基础上, 让头的前一个指向尾结点, 尾的后一个指向头结点    
     

// 注意: 
//  对于单链表和双链表而言
//  双向链表更浪费内存空间
//  双向链表根据下标查找性能是优于单链表的

2.2数组和链表的对比

数组和链表的插入，删除，随机访问操作的时间复杂度刚好相反。

① 数组使用的是连续的内存空间，可以利用CPU的高速缓存预读数据。链表的内存空间不是连续的，不能有效预读数据。当然如果数组过大，系统没有足够的连续内存空间，会抛出OOM
    (out of memory error)申请程序内存较大，虚拟机无法满足我们。

② 数组的缺点是大小固定，没法动态的调整大小。如果要存储一些对象，如果数组太大，浪费内存空间；如果数组太小，我们需要重新申请一个更大数组，并将数据拷贝过去，耗时。

③如果业务对内存的使用非常苛刻，数组更适合。因为结点有指针域，更消耗内存。而且对链表的频繁插入和删除，会导致结点对象的频繁创建和销毁，有可能会导致频繁的GC活动。

3, 线性表的实现

线性表根据定义 --> 有下标/位序的概念 --> 可以提供根据下标的操作(根据下标的增删改查)

二叉搜索树: 添加, 删除,查找, 修改

举例：实现单链表和双链表：

单链表：

/**
 * 第一个角度: 使用者,   实现的线性表是一个数据容器,
 * 第二个角度: 数据结构表现: 实现的线性表有下标操作
 * 第三个角度: 底层结构:  链表  (先用单链表)
 */
public class MyLinkedList {

    private Node head; // MyLinkedList底层持有的单链表的头结点
    private int size; // 用来保存我们这个线性表(外在表现), 存储了多少数据
    /**
     * 链表的添加
     * @param str : 要添加的元素
     * @return: 添加是否成功
     */
    public boolean add(String str) {

        // 判断链表在添加之前是否为空
        if (isEmpty()){
            // 如果原链表为空, 新添加的元素作为头结点存在
            head = new Node(str, null);
            size++;
            return true;
        }

        // 走到这, 意味着链表不空 --> 可以把这个新添加的元素, 放在链表尾部

        Node mid = head;
        while (mid.next != null){
            mid = mid.next;
        }
        mid.next = new Node(str, null);

        size++;

        return true;
    }

    /**
     * 根据内容在链表上删除元素
     * @param str: 要删除的元素
     * @return: 删除是否成功
     */
    public boolean remove(String str) {
        // 判断链表是否为空
        if (isEmpty())throw new RuntimeException("list is empty");

        if (str == null){
            // 删除的是否是头结点
            if (str == head.value){
                // 删除的是头结点
                head = head.next;
                size--;
                return true;
            }

            // 删除的是普通结点: 先找到这个要删除的结点, 再删除
            Node mid = head;
            // 如果mid之后不是null(后面还有元素可以遍历查找), 并且后面这个结点的value也不是要查找的值 --> 向后遍历
            while (mid.next != null  && str != mid.next.value ){
                mid = mid.next;
            }

            // 上述循环有两周跳出条件
            // 1, 没找到(遍历完了都没找到)
            if (mid.next == null)return false;
            // 2, 找到了 --> 删除mid.next
            mid.next = mid.next.next;
            size--;


        }else {
            // 删除的是否是头结点
            if (str.equals(head.value)){
                // 删除的是头结点
                head = head.next;
                size--;
                return true;
            }

            // 删除的是普通结点: 先找到这个要删除的结点, 再删除
            Node mid = head;
            // 如果mid之后不是null(后面还有元素可以遍历查找), 并且后面这个结点的value也不是要查找的值 --> 向后遍历
            while (mid.next != null  && !str.equals(mid.next.value)){
                mid = mid.next;
            }

            // 上述循环有两周跳出条件
            // 1, 没找到(遍历完了都没找到)
            if (mid.next == null)return false;
            // 2, 找到了 --> 删除mid.next
            mid.next = mid.next.next;
            size--;

        }

        return true;
    }

    /**
     * 查找某个元素是否存在
     * @param str:  要查找的元素
     * @return: 某个元素是否存在
     */
    public boolean contains(String str) {
        // 判断链表是否为空
        if (isEmpty())throw new RuntimeException("list is empty");

        Node mid = head;// 定义一个遍历结点

        //遍历结点不是null, 遍历结点的值不是要查找值 --> 向后遍历
        while (mid != null  && !str.equals(mid.value)){
            mid = mid.next;
        }

        // 遍历结点变成null --> 没有存储这个元素
        if (mid == null)return false;

        // 如果mid!=null , 一定找到了

        return true;
    }

    /**
     * 根据内容修改
     * @param oldValue : 要修改的值
     * @param newValue : 修改后的值
     * @return: 修改是否成功
     */
    public boolean set(String oldValue, String newValue) {
        // 判断链表是否为空
        if (isEmpty())throw new RuntimeException("list is empty");

        Node mid = head;// 定义一个遍历结点

        //遍历结点不是null, 遍历结点的值不是要查找值 --> 向后遍历
        while (mid != null  && !oldValue.equals(mid.value)){
            mid = mid.next;
        }

        // 遍历结点变成null --> 没有存储这个元素
        if (mid == null)return false;

        // 走到这意味着找到了
        mid.value = newValue;
        return true;
    }

    /**
     * 根据下标的添加方法
     * @param index : 要添加的位置
     * @param str : 要添加的内容
     * @return : 添加是否成功
     */
    public boolean add(int index, String str) {
        if(index < 0 || index > size) throw new IllegalArgumentException("index is Illegal ");

        // 要添加的位置是否是头位置
        if (index == 0){
            head = new Node(str, head);
            size++;
            return true;
        }


        // 根据下标查找位置, 添加
        Node mid = head; // 遍历结点指向引用
        int tag = 1; // 遍历的下标标记

        // tag != index:意味着还没有遍历到, 想添加的位置 --> 接着向后遍历
        while (tag != index){
            tag++;
            mid = mid.next;
        }

        // 经过上述 遍历: mid就是要添加位置之前的一个元素
        mid.next = new Node(str, mid.next);
        size++;

        return true;
    }

    /**
     * 根据下标删除内容
     * @param index: 要删除的下标位置
     * @return: 被删除的元素
     */
    public String remove(int index) {
        // 判断下标是否合法
        if(index < 0 || index >= size) throw new IllegalArgumentException("index is Illegal ");

        // 删除的是头元素
        if (index == 0){
            String oldValue = head.value;
            head = head.next;
            size--;
            return oldValue;
        }

        // 删除普通情况:
        // 根据下标找到对应结点, 删除

        // 根据下标查找位置
        Node mid = head; // 遍历结点指向引用
        int tag = 1; // 遍历的下标标记

        // tag != index:意味着还没有遍历到, 想添加的位置 --> 接着向后遍历
        while (tag != index){
            tag++;
            mid = mid.next;
        }

        // mid要查找下标的前一个位置
        String oldValue = mid.next.value;

        // 删除
        mid.next = mid.next.next;
        size--;
        return oldValue;
    }

    /**
     * 根据下标查找下标位置存储的元素
     * @param index : 要查找的下标位置
     * @return : 这个位置的元素
     */
    public String get(int index) {
        // 判断下标是否合法
        if(index < 0 || index >= size) throw new IllegalArgumentException("index is Illegal ");

        Node mid = head;
        int tag = 0;

        while (tag != index){
            tag++;
            mid = mid.next;
        }

        // mid 就是要查找的位置
        return mid.value;

    }

    /**
     * 根据下标修改
     * @param index : 要修改的下标位置
     * @param newValue : 新的值
     * @return: 旧的被替换的值
     */
    public String set(int index, String newValue) {
        // 判断下标是否合法
        if(index < 0 || index >= size) throw new IllegalArgumentException("index is Illegal ");

        Node mid = head;
        int tag = 0;

        while (tag != index){
            tag++;
            mid = mid.next;
        }

        // mid 就是要查找的下标位置
        String oldValue = mid.value;
        mid.value = newValue;

        return oldValue;
    }


    // 如下两个方法, 是一般作为一个数据容器都应该具有的方法
    public boolean isEmpty(){
        return  size == 0;
    }
    public int size(){
        return size;
    }


    /**
     * 单链表的结点
     */
    class Node{
        String value;
        Node next;

        public Node(String value, Node next) {
            this.value = value;
            this.next = next;
        }
    }

}

双向链表的实现：

/**
 * 用双向链表实现一个线性表
 *
 * 使用者: 数据容器
 * 数据结构: 线性表 --> 普通增删改查, 根据下标的增删改查
 * 底层结构: 双向链表
 */
public class MyDBLinkedList<T> {

    private Node head;// 双向链表的头结点
    private Node end; // 双向链表的尾结点
    private int size; // 存储的元素个数


    public boolean add(T value){

        // 判断双向链表是否为空
        if (isEmpty()){
            // 新元素, 既是头结点, 又是尾结点
            head = new Node(null, value, null);
            end = head;
            size++;
            return true;
        }

        // 如果链表不空, 这个新元素添加到尾部
        end.next = new Node(end, value, null);
        end = end.next;
        size++;

        return true;
    }

    public boolean remove(T value){
        // 判断链表是否为空
        if (isEmpty())throw new RuntimeException("list is empty");

        // 如果链表不空, 判断删除的是否是头结点
        if (value.equals(head.value)){
            // 删除的是头结点

            // 判断一下是不是这个链表中只剩这一个元素了
            if (size == 1){
                head = null;
                end = null;
                size = 0;
                return true;
            } else {
                // 链表中删除头结点, 还剩多个元素 -> 头结点后移
                head = head.next;
                head.pre = null;
                size--;
                return true;
            }
        }

        // 判断删除的是不是尾元素
        if (value.equals(end.value)){
            // 尾元素前移
            end = end.pre;
            end.next = null;
            size--;
            return true;
        }

        // 处理删除普通的中间结点
        Node mid = head;
        // 查找mid之后是否还有元素, 并且不是要找的
        while (mid.next != null && !value.equals(mid.next.value)){
           mid = mid.next;
        }

        // 有可能没有存储这个元素
        if (mid.next == null) return false;

        // 走到这: 意味着找到了, mid.next
        Node removeNode = mid.next;

        removeNode.next.pre = removeNode.pre;
        removeNode.pre.next = removeNode.next;
        size--;
        return true;
    }

    public boolean add(int index, T value){
        if (index < 0 || index > size) throw new IllegalArgumentException("size =" + size + "; index = " + index);

        // 判断添加位置是否是头位置
        if (index == 0){
            // 判断是否链表中没有任何元素
            if (isEmpty()){
                // 添加的元素既是头又是尾
                head = new Node(null, value, null);
                end = head;
                size++;
                return true;
            }else {
                // 链表中原本就存在元素
                Node newNode = new Node(null, value, head);
                head.pre = newNode;
                head = newNode;
                size++;
                return true;
            }
        }

        // 判断添加的是不是尾位置
        if (index == size){
          return add(value);
        }

        Node mid = head;

        // 添加的位置是中间位置
        if (index < size/2){// 偏头的位置

            // 从头向后遍历
            int tag = 1;
            while (tag != index){
                tag++;
                mid = mid.next;
            }

            // mid 是添加位置的前一个位置
        }else {// 偏尾的位置

            // 从尾向前遍历
            mid = end;
            int tag = size;
            while (tag != index){
                tag--;
                mid = mid.pre;
            }

            // mid 是添加位置的前一个位置
        }

        // 把元素添加到mid之后
        Node newNode = new Node(mid, value, mid.next);
        mid.next = newNode;
        newNode.next.pre = newNode;
        size++;

        return true;
    }

    public T remove(int index){
        // 下标范围检查
        if (index < 0 || index >= size) throw new IllegalArgumentException("size =" + size + "; index = " + index);

        // 删除的是头结点
        if (index == 0){
            T value = head.value;
            // 判断链表是不是仅剩一个元素
            if (size == 1){
                head = null;
                end = null;

            }else {
                head = head.next;
                head.pre = null;
            }
            size--;
            return value;
        }

        // 删除的是尾结点
        if (index == size-1){
            T value = end.value;
            end = end.pre;
            end.next = null;
            size--;
            return value;
        }

        // 删除的中间结点 --> 先找到要删除的结点,  再删除
        Node mid = head;

        // 添加的位置是中间位置
        if (index < size/2){// 偏头的位置

            // 从头向后遍历
            int tag = 1;
            while (tag != index){
                tag++;
                mid = mid.next;
            }
        }else {// 偏尾的位置

            // 从尾向前遍历
            mid = end;
            int tag = size;
            while (tag != index){
                tag--;
                mid = mid.pre;
            }
        }

        // mid 是查找位置的前一个位置
        Node removeNode = mid.next;
        removeNode.next.pre = removeNode.pre;
        removeNode.pre.next = removeNode.next;
        size--;


        return removeNode.value;
    }



    public boolean isEmpty(){
        return  size == 0;
    }
    public int size(){
        return size;
    }


    class Node{
        T value;// 值域
        Node pre;// 前指针域
        Node next;// 后指针域

        public Node(Node pre, T value, Node next) {
            this.value = value;
            this.pre = pre;
            this.next = next;
        }
    }
}

// 服务器

// 1, 服务器是一个物理电脑

// 2, 有的时候指的是一个运行在物理服务器的一段程序

4, 栈的实现

先用链表: push, pop, peek

/**
 * 使用单链表实现一个栈
 * push：入栈
 * pop：出栈
 * peek：查看栈顶元素
 */
public class MyLinkedStack <T> {

    private Node top; // 底层链表/栈的栈顶
    private int size;

    // 入栈操作
    public boolean push(T value){

        top = new Node(value, top);
        size++;

        return true;
    }

    // 出栈操作
    public T pop(){
        // 判断栈是否为空
        if (isEmpty())throw new RuntimeException("stack is empty");
        T value = top.value;
        top = top.next;
        size--;
        return value;
    }


    // 查看栈顶元素
    public T peek(){
        // 判断栈是否为空
        if (isEmpty())throw new RuntimeException("stack is empty");

        return top.value;
    }



    public boolean isEmpty(){
        return size == 0;
    }
    public int size(){
        return size;
    }

    class Node{
        T value;
        Node next;

        public Node(T value, Node next) {
            this.value = value;
            this.next = next;
        }
    }
}

用数组实现栈:

? 数组面临扩容问题

? 数组面临初始化的问题

/**
 * 用数组实现一个栈
 *
 * 使用者: 只是个数据容器, 提供添加和删除方法
 * 数据结构: 栈, 数据的出入顺序是有限定的
 * 底层结构: 数组
 */
public class MyArrayStack <T> {

    private final int INIT_CAPACITY = 10;
    private final int MAX_CAPACITY = Integer.MAX_VALUE - 8;

    private Object[]  objs; // 用数组实现一个栈的, 底层数组，数组的长度就是栈的容量，但不是存储元素的数量
    private int size ; // 数组中存储的元素数量

    /**
     * MyArrayStack的无参构造函数，创建一个大小为10的object栈
     */
    public MyArrayStack(){
        this.objs = new Object[INIT_CAPACITY];
        // this.objs = new Object[10];
    }

    /**
     * MyArrayStack的有参构造函数，创建一个大小为initCapacity的object栈
     * @param initCapacity：栈能存放的数据多少
     */
    public MyArrayStack(int initCapacity){
        if (initCapacity < 1 || initCapacity > MAX_CAPACITY) throw new IllegalArgumentException("parame is Illegal");
        this.objs = new Object[initCapacity];
    }

    // 性能
    // 1, 功能实现没有
    // 2, 代码可读性
    // 3, 性能问题
    // 解耦

    public boolean push(T value){
        // 判断数组是否满了, 如果满了, 需要扩容
        if (size == objs.length){
            // 需要扩容
            int newLen = getLen(); // 获取新的数组长度
            grow(newLen); // 根据新的长度扩容数组
        }

        // 走到这, 意味着数组是有空位置的 --> 存储
        objs[size] = value;
        size++;             //这两步是一体的，可以写成objs[size++] = value;
        return true;
    }
    
    // 根据旧长度, 获取一个新长度
    //特殊情况：1. 新长度不在合理区间内 2. 旧长度和新长度相等（原本的长度已经是最大值了）
    private int getLen() {
        // 旧长度
        int oldLen = objs.length;
        // 新长度
        int newLen = oldLen * 2;

        if (newLen > MAX_CAPACITY || newLen < 0){
            newLen = MAX_CAPACITY;
        }

        if (oldLen == newLen){// 如果这个条件满足, 意味着, 原本的长度已经是最大值了
           throw new RuntimeException(" stack can not add");
        }

        return newLen;
    }
    
    // 扩容: 把旧数组的数据转移到新数组
    private void grow(int newLen) {
        // 创建一个新数组
        Object[] newObjs = new Object[newLen];

        // 把旧数组的数据转移到新数组
        for (int i = 0; i < objs.length; i++) {
            newObjs[i] = objs[i];
        }

        objs = newObjs;
    }


    // 出栈方法
    public T pop(){
        if (isEmpty()) throw new RuntimeException("stack is empty");

        T oldValue = (T)objs[size - 1];

        // objs[size - 1] = null;
        size--;
        return oldValue;
    }

    // 查看栈顶元素
    public T peek(){
        if (isEmpty()) throw new RuntimeException("stack is empty");
        return (T)objs[size - 1];
    }
    
    //栈作为数据容器应该具有的两种方法
    public boolean isEmpty(){
        return size == 0;
    }
    public int size(){
        return size;
    }
}

5, 队列实现

先用链表: 单链表

/**
 * 使用单链表模拟一个队列
 * @param <T>
    // offer: 入归列
    // poll: 出队列
    // peek: 查看队头元素
 */
public class MyLinkedQueue <T> {


    private Node head;// 队列的头结点
    private Node end; // 队列的尾结点
    private int size;// 队列中存储的元素个数

    public boolean offer(T value){

        // 判断原链表是否为空
        if (isEmpty()){
            // 新添加的元素, 既是头结点, 又是尾结点
            head = new Node(value, null);
            end = head;
            size++;
            return true;
        }

        // 如果原链表不空, 新添加的结点在尾部
        end.next = new Node(value, null);
        end = end.next;
        size++;
        return true;
    }

    public T poll(){
        // 判断没有元素
        if (isEmpty()) throw new RuntimeException("queue is empty");

        // 如果仅剩一个元素
        if (size == 1){
            T  value = head.value;
            head = null;
            end = null;
            size--;
            return value;
        }

        // 如果链表有多个元素, 出头
        T  value = head.value;
        head = head.next;
        size--;
        return value;
    }

    public T peek(){
        // 判断没有元素
        if (isEmpty()) throw new RuntimeException("queue is empty");

        return head.value;
    }


    public boolean isEmpty(){
        return size == 0;
    }
    private int size(){
        return size;
    }

    class Node {
        T value; //值域
        Node next; // 下一个结点指向

        public Node(T value, Node next) {
            this.value = value;
            this.next = next;
        }
    }

}

用下数组:

注意一点：用链表实现队列时，里面的扩容方法是不能将数据直接一一对应的转移到新数组，因为有end和head指针，这样会使得后边一部分的元素为空：

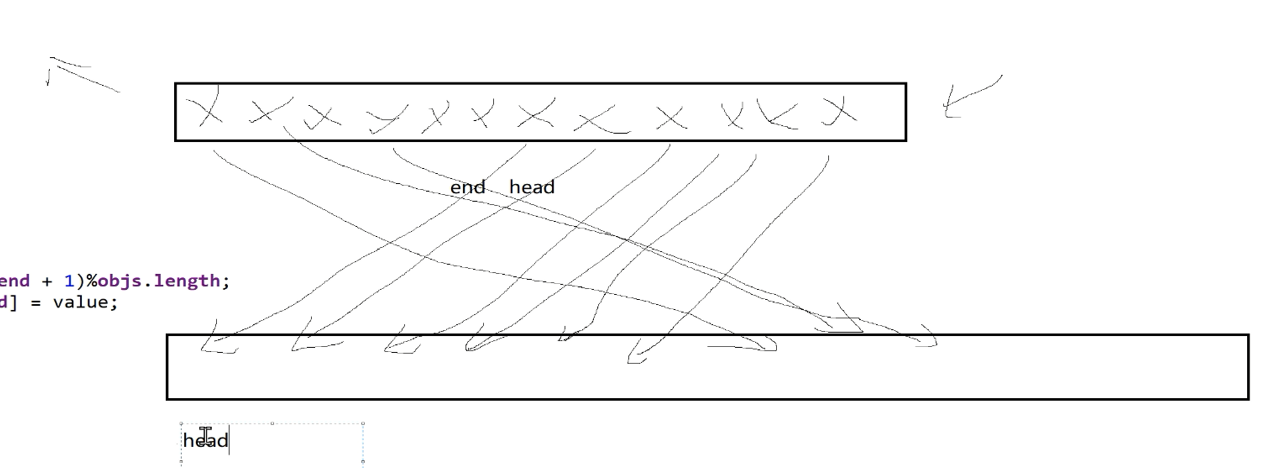
所以扩容的代码应该这样写：

private void grow(int newLen) {
    // 创建一个新数组
    Object[] newObjs = new Object[newLen];

    // 把旧数组的数据转移到新数组
    for (int i = 0; i < objs.length; i++) {
       //  newObjs[i] = objs[i];
        int tag = (head + i) % objs.length;

        newObjs[i] = objs[tag];
    }

    objs = newObjs;
    head = 0;
    end = size - 1;
}

总体的写法是这样的：

/**
 * 使用循环数组实现队列
 */
public class MyArrayQueue <T> {
    //队列的三种方法：
    // offer：增添
    // poll：删除
    // peek：返回值是头指针指向的元素

    private final int INIT_CAPACITY = 10;
    private final int MAX_CAPACITY = Integer.MAX_VALUE - 8;

    private Object[]  objs; // 用数组实现一个队列, 底层数组
    private int size ; // 数组中存储的元素数量

    private int head; // 在数组中队头的下标标记
    private int end; // 在数组中队尾的下标标记

    // 默认的构造方法
    public MyArrayQueue(){
        this.objs = new Object[INIT_CAPACITY];
    }
    // 指定长度的构造方法
    public MyArrayQueue(int initCapacity){
        if (initCapacity < 1 || initCapacity > MAX_CAPACITY) throw new  IllegalArgumentException("parame is Illegal");
        this.objs = new Object[initCapacity];
    }

    //入队操作
    //特殊情况：1. 容量太小：判断需要扩容
    public boolean offer(T value){

        if (size == objs.length){
            int newLen = getLen();
            grow(newLen);
        }
        // 走到这, 意味着数组有位置可以添加
        // 单独处理如果第一次添加(头和尾在一个地方)
        if (isEmpty()){
            objs[head] = value;
            end = head;
            size++;
            return true;
        }

        end = (end + 1)%objs.length;
        objs[end] = value;
        size++;
        return true;
    }

    private void grow(int newLen) {
        // 创建一个新数组
        Object[] newObjs = new Object[newLen];

        // 把旧数组的数据转移到新数组
        for (int i = 0; i < objs.length; i++) {
           //  newObjs[i] = objs[i];
            int tag = (head + i) % objs.length;

            newObjs[i] = objs[tag];
        }

        objs = newObjs;
        head = 0;
        end = size - 1;
    }
    private int getLen() {
        // 旧长度
        int oldLen = objs.length;
        // 新长度
        int newLen = oldLen * 2;

        if (newLen > MAX_CAPACITY || newLen < 0){
            newLen = MAX_CAPACITY;
        }

        if (oldLen == newLen){// 如果这个条件满足, 意味着, 原本的长度已经是最大值了
            throw new RuntimeException(" stack can not add");
        }

        return newLen;
    }


    public T poll(){
        if (isEmpty()) throw  new RuntimeException("queue is empty");

        // 单独处理一下仅剩一个元素的情况
        if (size == 1){
            T value = (T)objs[head];
            head = 0;
            end = 0;
            size --;
            return value;
        }

        T value = (T)objs[head];
        head = (head + 1)% objs.length;
        size--;
        return value;
    }

    //看头部节点
    public T peek(){
        if (isEmpty()) throw  new RuntimeException("queue is empty");
        return (T)objs[head];
    }



    public boolean isEmpty(){
        return  size == 0;
    }
}