算法原理
K -Means算法的工作原理:首先随机从数据集中选取K个点,每个点初始地代表每个簇的聚类中心,然后计算剩余各个样本到聚类中心的距离﹐将它赋给最近的簇﹐接着重新计算每簇的平均值﹐整个过程不断重复,如果相邻两次调整没有明显变化,说明数据聚类形成的簇已经收敛。本算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确。若不正确﹐就要调整,在全部样本调整完后,再修改聚类中心,进入下一次迭代。这个过程将不断重复直到满足某个终止条件,终止条件可以是以下任何一个:
- 没有对象被重新分配给不同的聚类。
- 聚类中心不再发生变化。
- 误差平方和局部最小。
K- Means算法步骤
- 从N个数据对象任意选择K个对象作为初始聚类中心。
- 循环③到④直到每个聚类不再发生变化为止。
- 根据每个聚类对象的均值(中心对象),计算每个对象与这些中心对象的距离,并根据最小距离重新对相应对象进行划分。
- 重新计算每个聚类的均值(中心对象),直到聚类中心不再变化。这种划分使得下式最小:

K- Means算法特点
- 在K - Means算法中K是事先给定的,这个K值的选定是非常难以估计的。
- 在K-Means算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。
- K-Means算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的。
- K-Means算法对一些离散点和初始K值敏感,不同的距离初始值对同样的数据样本可能得到不同的结果。
K- Means算法应用一:样本特征聚类
已知有20个样本,每个样本有2个特征,数据分布如表3-5所列,试对这些数据进行分类。

matlab代码为:
% K-means 算法MATLAB实现
%--------------------------------------------------------------------------
%% 数据准备和初始化
clc
clear
x=[0 0;1 0; 0 1; 1 1;2 1;1 2; 2 2;3 2; 6 6; 7 6; 8 6; 6 7; 7 7; 8 7; 9 7 ; 7 8; 8 8; 9 8; 8 9 ; 9 9];
z=zeros(2,2);
z1=zeros(2,2);
z=x(1:2, 1:2);
%% 寻找聚类中心
while 1
count=zeros(2,1);
allsum=zeros(2,2);
for i=1:20 % 对每一个样本i,计算到2个聚类中心的距离
temp1=sqrt((z(1,1)-x(i,1)).^2+(z(1,2)-x(i,2)).^2);
temp2=sqrt((z(2,1)-x(i,1)).^2+(z(2,2)-x(i,2)).^2);
if(temp1<temp2)
count(1)=count(1)+1;
allsum(1,1)=allsum(1,1)+x(i,1);
allsum(1,2)=allsum(1,2)+x(i,2);
else
count(2)=count(2)+1;
allsum(2,1)=allsum(2,1)+x(i,1);
allsum(2,2)=allsum(2,2)+x(i,2);
end
end
z1(1,1)=allsum(1,1)/count(1);
z1(1,2)=allsum(1,2)/count(1);
z1(2,1)=allsum(2,1)/count(2);
z1(2,2)=allsum(2,2)/count(2);
if(z==z1)
break;
else
z=z1;
end
end
%% 结果显示
disp(z1);% 输出聚类中心
plot( x(:,1), x(:,2),'k*',...
'LineWidth',2,...
'MarkerSize',10,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.5,0.5])
hold on
plot(z1(:,1),z1(:,2),'ko',...
'LineWidth',2,...
'MarkerSize',10,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.5,0.5])
set(gca,'linewidth',2) ;
xlabel('特征x1','fontsize',12);
ylabel('特征x2', 'fontsize',12);
title('K-means分类图','fontsize',12);
运行结果:
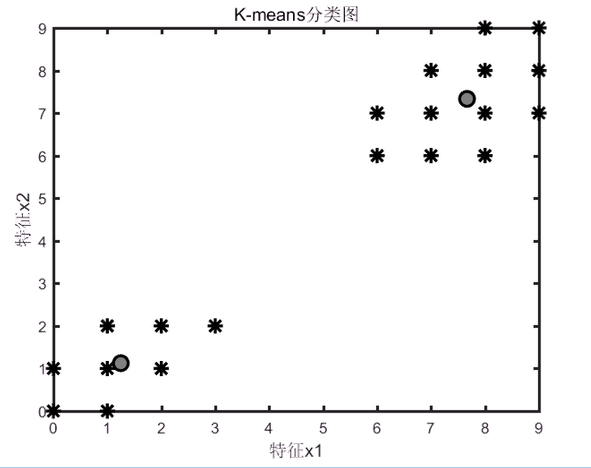
很明显已经聚类成功,效果很好。聚类算法,不是分类算法。分类算法是给一个数据,然后判断这个数据属于已分好的类中的具体哪一类。聚类算法是给一大堆原始数据,然后通过算法将其中具有相似特征的数据聚为一类。
聚类分析引用二:西瓜数据聚类分析
我们在这里讲一下:evalclusters 的使用,它专门评估集群解决方案。
语法:
eva = evalclusters(x,clust,criterion)
eva = evalclusters(x,clust,criterion,Name,Value)
参数讲解:
- x—输入数据
- clust—聚类算法,可以传:
'kmeans' x使用聚类算法对数据进行kmeans聚类,'EmptyAction'设置为'singleton'和。'Replicates'5
'linkage' x使用凝聚聚类算法对数据进行clusterdata聚类,'Linkage'设置为'ward'.
'gmdistribution' x使用gmdistribution高斯混合分布算法对数据进行聚类,'SharedCov'设置为true并'Replicates'设置为 5。
- criterion—聚类评价标准

- KList-要评估向量的集群数量列表
要评估的集群数列表,指定为逗号分隔的对组,由 ‘KList’和 一个正整数值向量组成。您必须指定 KList何时clust是聚类算法名称或函数句柄。当criterionis 时’gap’,clust必须是字符向量、字符串标量或函数句柄,并且必须指定 KList。
例子: ‘KList’,[1:6]
西瓜数据聚类代码如下,data为数据:
clear all
clc
data = [0.697 0.460;0.774,0.376;0.634,0.264;0.608,0.318;0.556,0.215;0.403,0.237;
0.481,0.149;0.437,0.211;0.666,0.091;0.243,0.267;0.245,0.057;0.343,0.099;
0.639 0.161;0.657,0.198;0.360,0.370;0.593,0.042;0.719,0.103;0.359,0.188;
0.339,0.241;0.282,0.257;0.748,0.232;0.714,0.346;0.483,0.312;0.478,0.437;
0.525,0.369;0.751,0.489;0.532,0.472;0.473,0.376;0.725,0.445;0.446,0.459;]
rng('default'); % For reproducibility
eva = evalclusters(data,'kmeans','CalinskiHarabasz','KList',[1:10])
plot(eva)
结果如下:
eva = CalinskiHarabaszEvaluation (具有属性):
NumObservations: 30
InspectedK: [1 2 3 4 5 6 7 8 9 10]
CriterionValues: [NaN 22.897827855713349 27.920710464673380 34.716174547230231 33.043649120249157 32.769237014072786 33.072286850654820 31.674595193797927 33.455700482758587 31.042092727593104]
OptimalK: 4
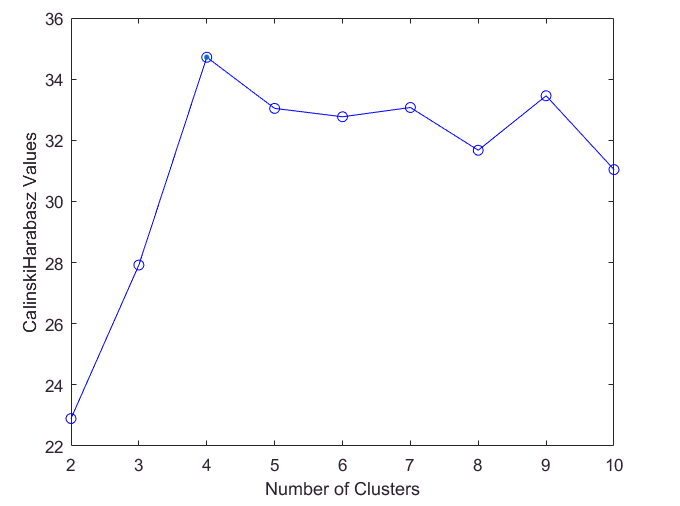
OptimalK: 4,k=4是比较合适的,根据CH指标越大越好的准则,k=4有最好的结果。
参考文献
- https://ww2.mathworks.cn/help/stats/kmeans.html
- https://ww2.mathworks.cn/help/stats/evalclusters.html?s_tid=doc_ta