[数据结构与算法]22.1.27~28

1.reverse一个数组是用下标的，reverse（a,a+n);注意字符串数组（char）也属于数组；

2.reverse一个string s，reverse(s.begin(),s.end());

3.INF 无穷大

4.最长公共子序列

f[i][j]表示a数组的第i个和b数组的第j个的方案数；

如果a[i]==b[j]，f[i][j]=f[i-1][j-1]+1;如图所示，如果两个字符相等，可以直接转化成f[i-1][j-1];

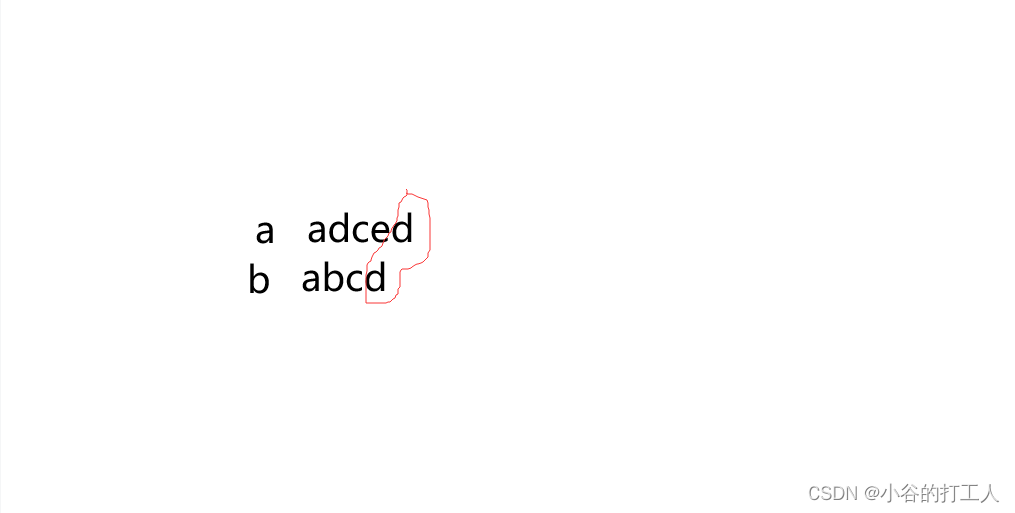
不相等的话，两个字符一定有一个可以抛弃，可以对f[i-1][j],f[i][j-1]两种状态取max来转移。

?

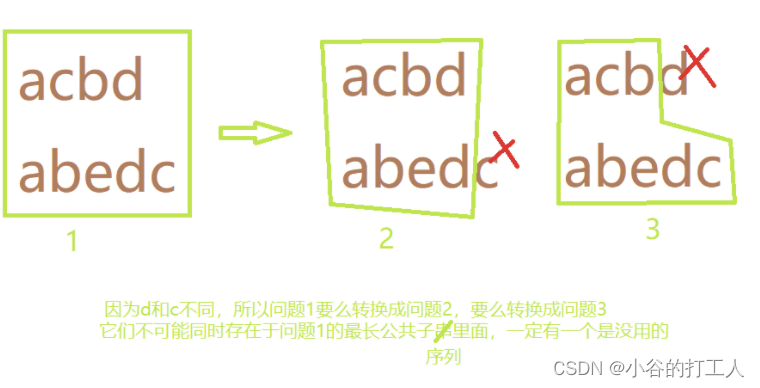
#include<bits/stdc++.h>
#define rep1(i,a,n) for(int i=a;i<n;i++)
#define rep2(i,a,n) for(int i=a;i<=n;i++)
#define per1(i,n,a)	for(int i=n;i>a;i--)
#define per2(i,n,a) for(int i=n;i>=a;i--)
using ll=long long ;
using namespace std;
const int N=1e5+10;
const int mod=1e9+7;
int n,m;
char a[1100],b[1100];
int f[1100][1100];
int main()
{	
	cin>>n>>m;
	cin>>a+1;
	cin>>b+1;
	rep2(i,1,n){
		rep2(j,1,m){
			if(a[i]==b[j])f[i][j]=f[i-1][j-1]+1;
			else{
				f[i][j]=max(f[i-1][j],f[i][j-1]);
							}
		}
	}
	cout<<f[n][m]<<endl;
	return 0;		 
}

5.数字三角形二刷

这次用标准的分析顺序去做，下标含义，走i，j的路径上的最大和；初始化：要思考范围问题；

f[1][1]=a[1][1];遍历顺序及条件，从第二层开始；寻找最大值；这几步时标准的dp顺序做法；

有时有的题目初始化不用刻意，寻找最大值可以省略（看你的写法）；

#include<bits/stdc++.h>
#define rep1(i,a,n) for(int i=a;i<n;i++)
#define rep2(i,a,n) for(int i=a;i<=n;i++)
#define per1(i,n,a)	for(int i=n;i>a;i--)
#define per2(i,n,a) for(int i=n;i>=a;i--)
using ll=long long ;
using namespace std;
const int N=1e5+10;
const int mod=1e9+7;
int f[1100][1100];
int a[1100][1100];
int main()
{	
	int n;
	cin>>n;
	rep2(i,1,n)
	rep2(j,1,i)scanf("%d",&a[i][j]);
	rep2(i,1,n)
	rep2(j,0,i+1)f[i][j]=INT_MIN;//初始化dp数组
	f[1][1]=a[1][1];
	rep2(i,2,n)
	rep2(j,1,i)
	f[i][j]=a[i][j]+max(f[i-1][j-1],f[i-1][j]);
	int ans=INT_MIN;
	rep2(i,1,n)ans=max(ans,f[n][i]);
	cout<<ans;
	
	return 0;		 
}