[数据结构与算法]leetcode671. 二叉树中第二小的节点

1.题目描述：

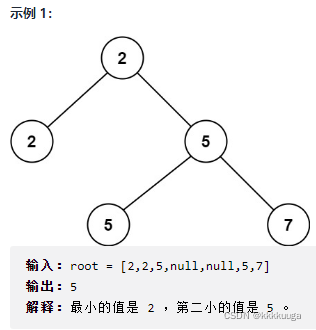
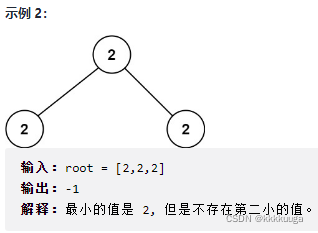
给定一个非空特殊的二叉树，每个节点都是正数，并且每个节点的子节点数量只能为2或0。如果一个节点有两个子节点的话，那么该节点的值等于两个子节点中较小的一个。更正式地说，即root.val = min(root.left.val, root.right.val)总成立。给出这样的一个二叉树，你需要输出所有节点第二小的值。如果第二小的值不存在的话，输出-1。

2.递归+集合排序：

递归遍历所有节点的值，存入集合中，再对集合排序取出第二小的节点，这种做法没有利用此题中节点的特殊性，代码易懂如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    List<Integer> list = new ArrayList<>();
    public int findSecondMinimumValue(TreeNode root) {
        dfs(root);
        int size = list.size();
        if (size == 0 && size == 1) return -1;
        Collections.sort(list);
        int i = 1;
        while (i < size && list.get(0).equals(list.get(i))) i++;//-128到127之外未缓存使用==比较地址值
        if (i == size) return -1;
        return list.get(i);
    }
    public void dfs(TreeNode root) {
        if (root == null) return;
        list.add(root.val);
        if (root.left != null) dfs(root.left);
        if (root.right != null) dfs(root.right);
    }
}

3.深搜递归：

class Solution {
    int res = -1;//使用res记录除根结点外的最小值，初值为-1
    int rootvalue;
    public int findSecondMinimumValue(TreeNode root) {
        rootvalue = root.val;
        dfs(root);
        return res;
    }
    public void dfs(TreeNode node) {
        if (node == null) return;
        if (res != -1 && node.val >= res) return;//res更新后若遇到更大值，无需更新res
        if (node.val > rootvalue) res = node.val;//更新res
        dfs(node.left);
        dfs(node.right);
    }
}

class Solution {
    int res = -1;
    public int findSecondMinimumValue(TreeNode root) {
        dfs(root, root.val);
        return res;
    }
    public void dfs(TreeNode root, int cur) {
        if (root == null) return;
        if (root.val != cur) {
            if (res == -1) res = root.val;
            else res = Math.min(res, root.val);//较容易理解的递归
            return;
        }
        dfs(root.left, cur);
        dfs(root.right, cur);
    }
}

4.广搜层序遍历：

class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        if (root == null) return -1;
        int res = Integer.MAX_VALUE;
        boolean flag = false;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                TreeNode temp = queue.poll();
                if (temp.val != root.val) {
                    res = Math.min(res, temp.val);//实际是得到除根节点外的最小节点
                    flag = true;//不用flag而用res==Integer.MAX_VALUE时节点值为Integer.MAX_VALUE的示例通不过
                } 
                if (temp.left != null) queue.offer(temp.left);
                if (temp.right != null) queue.offer(temp.right);
            }
        }
        return flag == true ? res : -1;
    }
}