[数据结构与算法]Grid Xor（构造/贪心）

题目
题意：现在有一个$n?n$的数组$a$（$n$为偶数），但是丢失了它的数据，我们只知道，每个元素的相邻元素的异或和，构成的数组$b$。相邻元素是指，元素的上下左右相邻的元素。现在已知$b$，求原数组$a$的所有元素的异或和。

参考Adityakumar007的提交代码。

思路：求$b$所有元素的异或和，肯定会重复计算。我们可以遍历数组$b$，在计算当前元素$b_{ij}$之前，先判断它贡献的相邻元素$a[i?1][j],a[i+1][j],a[i][j?1],a[i][j+1]$，是否别的$b$元素已经贡献过。如果贡献过，则当前的$b_{ij}$不加进来。

通过这个策略，我们可以保证每个$a_{ij}$元素只会贡献一次。同时，每个$a_{ij}$都会被统计进来。

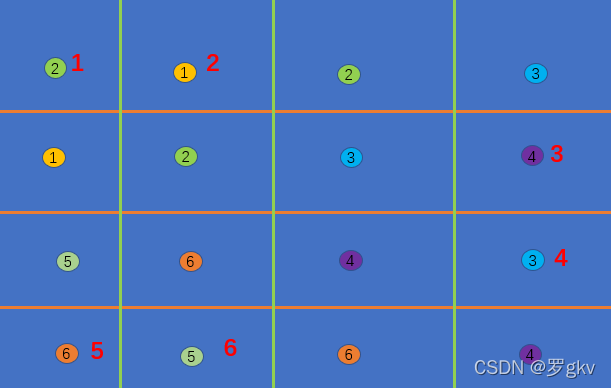
如图4x4的例子，红色数字表示遍历过程中有效的$b$位置，圆圈数字表示每个有效$b$位置的贡献点，我们可以看到，所有位置都有一个贡献点。严格证明不会，就拿图片感性理解，凑合下吧_(:з」∠)_

#include<bits/stdc++.h> 
using namespace std;
const int maxn = 1010;
#define ll long long

int n;
int a[maxn][maxn];
bool vis[maxn][maxn];
int dx[] = {0, 0, 1, -1};
int dy[] = {1, -1, 0, 0};

bool check(int x, int y) {
	bool flag = 1;// 判断贡献的位置，是否别人已经贡献过 
	for (int i = 0; i < 4; ++i) {
		int xx = x + dx[i];
		int yy = y + dy[i];
		if (xx >= 0 && xx < n && yy >= 0 && yy < n) {
			flag = flag && !vis[xx][yy];
		} 
	}
	if (!flag) {
		return false;
	}
	// 更新当前元素，所有的贡献位置 
	for (int i = 0; i < 4; ++i) {
		int xx = x + dx[i];
		int yy = y + dy[i];
		if (xx >= 0 && xx < n && yy >= 0 && yy < n) {
			vis[xx][yy] = true;
		} 
	}
	return true;
}
void solve() {
	scanf("%d", &n);
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			scanf("%d", &a[i][j]);
			vis[i][j] = 0;
		} 
	} 
	int ans = 0;
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			if (check(i, j)) {
				ans ^= a[i][j];
			}
		} 
	} 
	printf("%d\n", ans);
}

int main() {
	int t;
	scanf("%d", &t);
	while (t--) {
		solve();
	}
}