记录一下,算法题中频繁使用到的算法代码块逻辑思路,学习的课程来自b站链接:清华大学博士讲解Python数据结构与算法(完整版)全套100节
汉诺塔问题
大梵天创造世界时造了三根金钢石柱子,其中一根柱子自底向上叠着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
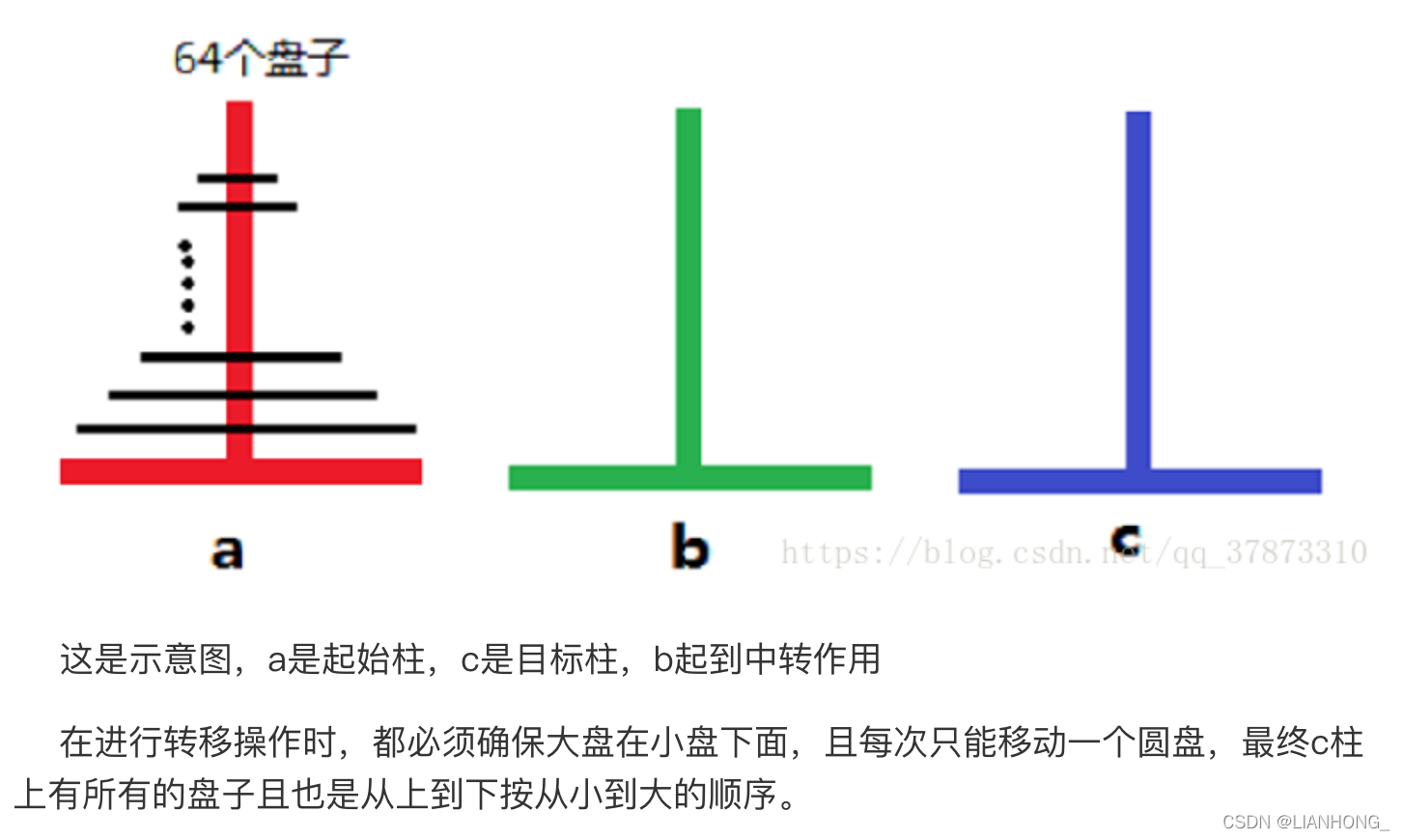
# 其实是递归的问题
def hanoi(n,a,b,c): # n指几个,a b c指从a跟柱子出发经过b跟柱子到达c跟柱子,
if n > 0: #能够移动的盘子肯定要>0
hanoi(n-1,a,c,b) #把n-1个盘子从A经过C移动到B
print("moving form %s to %s"% (a,c))
hanoi(n-1,b,a,c) #把n-1个盘子从B经过A移动到C
hanoi(3,'A','B','C') #A B C 三根柱子
顺序查找
时间复杂度:O(N)
def linear_search(li, val):
for ind, v in enumerate(li):
if v == val:
return ind
else:
return None
print(linear_search([1,7,6,5,4,2,3,4,0],0)) #8
二分查找
前提是列表有序,时间复杂度为O(logN)
def binary_search(li, val):
left = 0
right = len(li) -1
while left <= right: #候选区有值
mid = (left + right) // 2
if li[mid] == val :
return mid
elif li[mid] > val: #待查找的值在mid左侧
right = mid - 1
else:
left = mid + 1 #待查找的值在mid右侧
else:
return None
冒泡排序Bubble Sort
原地排序,列表中每两个相邻的数,如果前面比后面大,则交换这两个数(升序)
时间复杂度:O(N)
def buble_sort(li):
for i in range(len(li)-1): #第i趟
for j in range((len(li)-i-1)):
if li[j] > li[j+1]:
li[j], li[j+1] = li[j+1], li[j]
选择排序
原始时间复杂度:O(N2)
#原始
def select_sort_simple(li):
li_new = []
for i in range(len(li)):
min_val = min(li)
li_new.append(min_val)
li.remove(min_val)
return li_new
li = [3,5,1,2,6,8,2,6]
print(select_sort_simple(li))
#优化
def select_sort(li):
for i in range(len(li) -1): # i是第几趟
min_loc = i
for j in range(i+1,len(li)-1):
if li[j] < li[min_loc]:
min_loc = j
li[i],li[min_loc] = li[min_loc], li[i]
插入排序
原始时间复杂度:O(N2)
def insert_sort(li):
for i in range(1,len(li)): # i 表示摸到的牌的下标
temp = li[i]
j = i - 1 #指手中的牌
while li[j] > temp and j >= 0:
li[j+1] = li[j]
j -= 1
li[j+1] = temp
快速排序
取一个元素p,使元素p归位,列表分为两部分,左边比p小,右边比p大,递归完成排序
原始时间复杂度:O(nlogn)
def partition(li,left,right):
tmp = li[left]
while left < right:
while left < right and li[right] >= tmp: #从右面找出比tmp小的数
right -= 1 #往左走一步
li[left] = li[right] #右边的空位填入tmp值
while left < right and li[left] <= tmp:
left += 1
li[right] = li[left] #把左边的值写到右边空位上
li[left] = tmp # tmp归位
return left
def quick_sort(li,left,right):
if left < right:
mid = partition(li,left,right)
quick_sort(li,left,mid-1)
quick_sort(li,mid+1,right)
li = [3,4,6,7,1,2,3,8,9]
quick_sort(li,0,len(li)-1)
print(li)