[数据结构与算法]Codeforces Round #767 (Div. 2) E~F2

1629E - Grid Xor

题目描述：

给出一个 $n?n$ 的矩阵 $a$，其中有 $a_{i,j}$ 代表 $(i,j)$ 相邻元素的异或和，当 $(k,l)$ 满足 $|i?k|=1\&j=l$ 或 $i=k\&|j?l|=1$ 时，$(k,l)$ 为 $(i,j)$ 的相邻元素，求矩阵 $a$ 所有元素的异或和

$1\le n\le 1000$

solution:

可以把 $a_{i,j}$ 想象成对相邻元素染色，并且只有奇数次染色才能把成功染色，考虑如何把所有格子染色，有很多做法：

以下部分做法参考自洛谷用户

做法1：

我们一行行地去做，每次保证当前行的上一行全部染色奇数次，这种情况下能保证完全染色。证明略。

做法2：

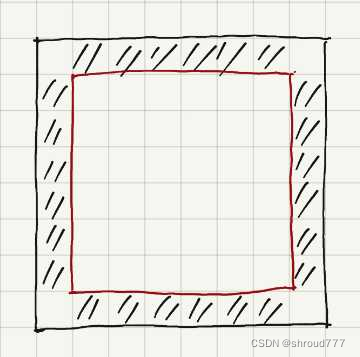
我们可以构造出上图这种类似三角形的染色，我们可以旋转并缩小尺寸覆盖所有格子

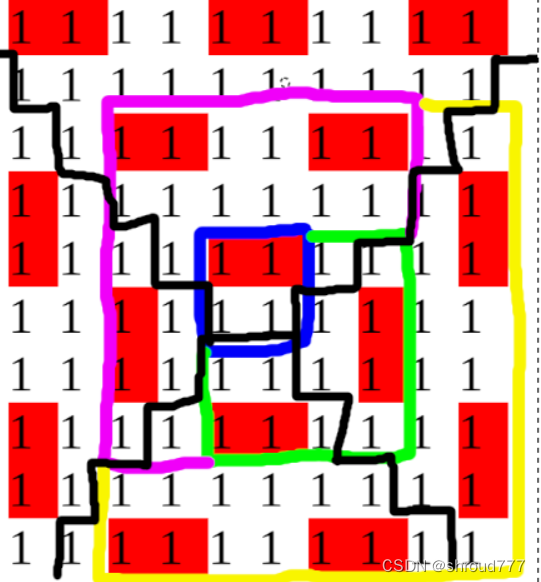
做法3：

如果我们把对矩阵中的所有格子操作，那么可以得到如下染色情况：

类似的，我们缩小染色范围，可以不断缩小直到一个 $4\times 4$ ，就是以下情况：

发现剩余类似对角线剩余，考虑用以下方法染色：

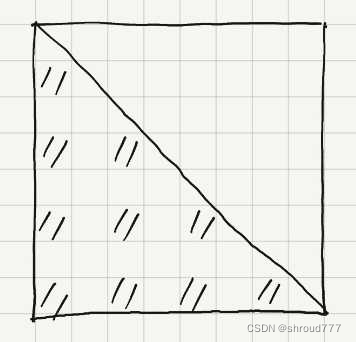
上述构造思路就是先把类对角线不重不漏地染色，然后发现对角线往下移动了，以此类推

做法4：

此方法来自于 wsyear

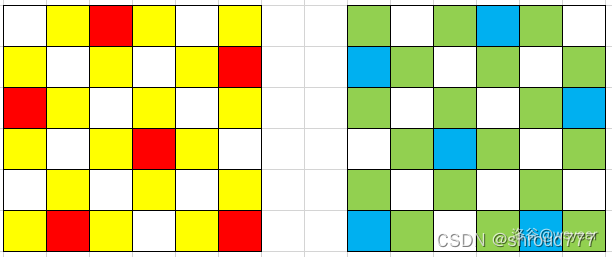
上述两者染色情况地交集就是整个矩阵，考虑推广到 $8\times 8$ 观察变化

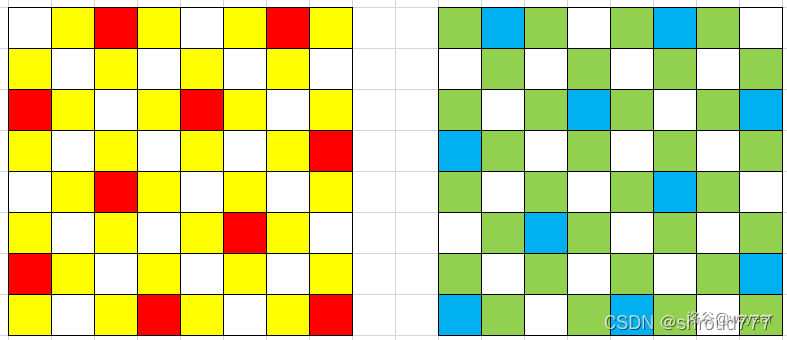
可以发现上述红点与蓝点关于某竖线对称，对于红点 $(i,j)$ 必然存在蓝点 $(i,n?j+1)$

观察 $8\times 8$ 的红点位置：

$(1,3)，(3,1)$
$(1,7)，(3,5)，(5,3)，(7,1)$
$(4,8)，(6,6)，(8,4)$
$(8,8)$

发现每组红点横坐标差为 $2$，横纵坐标之和前两组小于等于 $n$，后两组大于等于 $n$，规律同样适用于 $6\times 6$

1629F1 - Game on Sum (Easy Version)

题目描述：

Alice 和 Bob 进行 $n$ 场游戏，初始得分为 $0$，Alice 想要最大化得分，而 Bob 想要最小化。对于每轮游戏，Alice 从 $[0,k]$ 中人选一个实数，Bob 可以选择得分加上或减去这个数字，所有 $n$ 轮游戏中 Bob 至少在 $m$ 轮中选择加上 Alice 给出的数。问在双方都进行最优操作的情况下，最终得分该是多少？

$1\le m\le n\le 2000,0\le k\le 10^9+7$

solution:

在本轮游戏 Bob 可能进行的操作未知的情况下，Alice 必然不可能选择过大或过小的实数。

具体地，我们可以考虑 $n=2,m=1$ 的情况，假设 Alice 在第一轮中选的数是 $x$，那么如果 $x$ 很小，Bob 会选择加上 $x$，下一轮必然是减操作，那么 Alice 肯定会选 $0$。如果 $x$ 很大，那么 Bob 会减去 $x$，下一轮必然是加操作，那么 Alice 肯定会选 $k$。

因此在 Alice 想要最大化分数，Bob 想要最小化分数的情况下，Alice 会选择一个合适的数 $x$ 使得 $\min (x,k?x)$ 最大，显然在 $x=\frac{k}{2}$ 时最优。

对于任意的 $n,m$（我们只考虑这两个因素），我们考虑DP，设 $f_i,j$ 代表 $i$ 场比赛，至少 $j$ 次加法情况下的最终分数。因为两人绝顶聪明使得当前决策 仅 基于接下来的决策。

综上，可以发现一般博弈论的 DP 题都是 从后往前 DP，即从确定的终止状态向初始状态 DP，因为 绝顶聪明 这一条件使得双方都能预测到他们当前的行为对后续局面的影响，可以说只有 后效性 而没有 前效性：若 $i,j$ 确定，则两人之前的决策对当前决策无影响。

可以发现上述DP状态本质是 Bob 决策的过程，因此最优解应该是最小值，但此时不确定 Alice 提供的数，先设其为 $x$，那么有 $$f_{i,j}=\min (f_{i?1,j?1}+x,f_{i?1,j}?x)$$可以发现转移方程类似我们一开始的问题，显然有 $x=\frac{f_{i?1,j}?f_{i?1,j?1}}{2}$，因此转移方程为：$$f_{i,j}=\frac{f_{i?1,j}+f_{i?1,j?1}}{2}$$易知，$f_{i,0}=0,f_{i,i}=i?k$ 为边界条件，复杂度 $\mathcal{O}(n^2)$

code:

#include <bits/stdc++.h>

using namespace std;

const int maxn=2050;
const int p=1e9+7;

typedef long long ll;

ll f[maxn][maxn];
int n,m,k;

int qpow(int a,int b){
    int res=1;
    while(b){
        if(b&1) res=1ll*res*a%p;
        a=1ll*a*a%p;
        b>>=1; 
    }
    return res;
}

int main(){
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--){
        cin>>n>>m>>k;
        for(int i=1;i<=n;i++) f[i][0]=0,f[i][i]=1ll*i*k%p;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=min(i-1,m);j++){
                int x=1ll*(f[i-1][j]-f[i-1][j-1])*qpow(2,p-2)%p;
                f[i][j]=min(f[i-1][j-1]+x+p,(f[i-1][j]-x+p))%p;
            }
        }
        cout<<f[n][m]<<endl;
    }


    return 0;
}

1629F2 - Game on Sum (Hard Version)

题目描述：

题面同 Easy Version，数据变为： $1\le m\le n\le 10^6$

solution:

考虑优化DP。
$$f_{i,j}=\frac{f_{i?1,j}+f_{i?1,j?1}}{2}$$
上述转移方程容易让我们联想到杨辉三角预处理组合数，但是每次转移还有一个系数，可以发现所有非边界的合法状态的转移都来自边界状态，我们考虑对于 $f_{n,m}$ 来自边界的贡献。

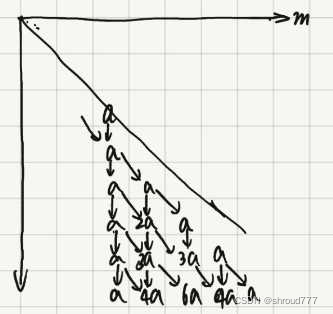
感性参考上图，从 $(i,i)$ 到 $(n,m)$ 一共下行 $n?i$ 次，其中我们需要在这 $n?i$ 次中选择 $m?i$ 次右下行，并且由于 $(i,i)$ 的特殊性（第一次只能往下，右下是别的边界），实际情况共有 $\left(\genfrac{}{}{0ex}{}{n?i?1}{m?i}\right)$ 种，并且每条路线都会衰减 $\frac{1}{2^{n?i}}$，因此贡献就是：$$\sum _{i=1}^m\frac{ik\left(\genfrac{}{}{0ex}{}{n?i?1}{m?i}\right)}{2^{n?i}}$$复杂度 $\mathcal{O}(n)$

code:

#include <bits/stdc++.h>

using namespace std;

const int maxn=1e6+10;
const int p=1e9+7;

typedef long long ll;

int n,m,k;
ll ans,fac[maxn],ifac[maxn];

int qpow(int a,int b){
    int res=1;
    while(b){
        if(b&1) res=1ll*res*a%p;
        a=1ll*a*a%p;
        b>>=1; 
    }
    return res;
}

inline ll C(int n,int m){
    if(n<m) return 0;
    return fac[n]*ifac[m]%p*ifac[n-m]%p;
}

int main(){
    ios::sync_with_stdio(false);
    fac[0]=1;
    for(int i=1;i<=1000000;i++) fac[i]=fac[i-1]*i%p;
    ifac[1000000]=qpow(fac[1000000],p-2);
    for(int i=1000000-1;i>=0;i--) ifac[i]=ifac[i+1]*(i+1)%p;
    int t;
    cin>>t;

    while(t--){
        cin>>n>>m>>k;
        if(n==m){
            cout<<1ll*k*n%p<<endl;
            continue;
        }
        if(m==0){
            cout<<0<<endl;continue;
        }
        ll ans=0;
        for(int i=1;i<=m;i++){
            ans=(ans+1ll*i*k%p*C(n-i-1,m-i)%p*qpow(qpow(2,n-i),p-2)%p)%p;
        }
        
        cout<<ans<<endl;
    }


    return 0;
}