[数据结构与算法] 1.2（1）欧拉方法

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 1.2（1）欧拉方法 -> 正文阅读

[数据结构与算法]1.2（1）欧拉方法

让我们简单思考（ODEs）（1.1）的含义。可以得到以下两条信息：我们知道 $y$ 在一个初值点 $t$ = $t_0$ 处的值，并且给任何函数 $y$ $\epsilon$ $\mathbb{R}^{d}$ 和时间 $t\geq t_0$ ，我们就能得到微分方程的斜率。这样做的目的是使我们能够估计出 $y$ 在其他点的值，最简单的方法是用线性插值，换句话说，我们通过做这样的近似 $f\left ( t,y\left ( t \right ) \right )\approx f\left ( t_0,y\left ( t_0 \right ) \right )\$ ， $t\epsilon \left [ t_0,t_0+h \right ]$ 来估计 $y\left ( t \right )$ 的值，当 $h> 0$ 足够小时，结合（1.1），

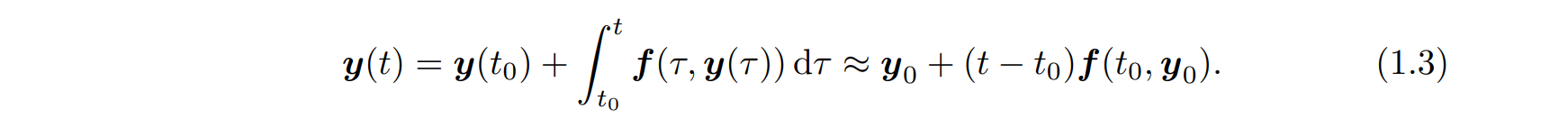
给出一系列 $t_0$ ， $t_1= t_0+ h$ ，? $t_2=t_1+2h$ ,...,其中 $h> 0$ 是步长，我们用 $y_n$ 表示精确解 $y(t_n)$ , $n=1,2,...$ 的数值近似解，由式（1.3），我们采取

$y_1=y_0+hf(t_0,y_0)$ .

这个过程能够持续输出在 $t_2,t_3$ ,...处 $y$ 的近似解。通常我们能够得到一个递归式

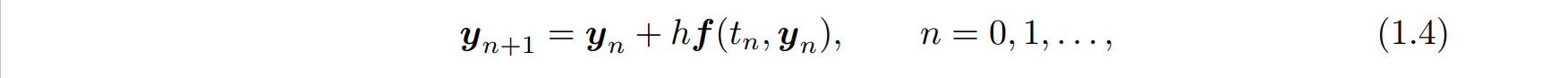
这就是著名的欧拉方法。?

欧拉方法尽管很简单，却有着持久的实用意义，它不仅是最基本的（ODEs）计算式，而且也是微分数值分析发展的基础。更深层次的理解为，对于所有的多步式和龙格-库塔式，我们没有其他需要讨论的，只需讨论式（1.4）即可。

图解? ? ?欧拉方法能够用图形形象的表示出来，例如，考虑这个标量逻辑斯谛方程 $y^{?{}'}=y(1-y)$ , $y\left ( 0 \right )=1/10$ .

图一展示了欧拉方法最初的几步，用了一个很大的步长为 $h=1$ ，并且在每一步我们都能得出 $t_n=nh$ 附近 $y\left ( t_n \right )=y_n$ 的精确解，和关于欧拉方程的（1.4）的线性插值。

这个被定义的初始条件是准确的，因此是 $t_0$ 处准确的斜率。可是这些数值解不是一条弯曲的轨迹而是分段线性的。可以看到 $t_1$ 处是错误的轨迹，也就是说 $t_1$ 处的斜率是错误的——或者说是别的，但它是这个错误结果的正确的斜率。继续做下去，轨迹可能会越来越偏离原来的轨迹。

可是，求数值解的实际目标不是这样的，所以要去尽量避免错误。毕竟，我们要做近似解，但因为一开始并不知道精确解，并且误差在我们求（ODEs)近似解的每一步都可能产生，我们的目的是要去理解这些过程并确保没有错误。在这个被求解的例子中，误差累积并没有超出容忍范围。很显然，过大的步长 $h=1$ 只导致了图1.1中的局部误差。