动态规划基础
动态规划类型的题目种类其实并不多,这里只讲简单的DP,各种DP之间划分界限也没那么明显,所以只是一个大概的划分,重要的是学会思想。
我理解的动态规划:绝妙的状态表示+不重不漏的状态转移,我感觉最难的还是如何表示状态,这里简单介绍一些常用的模型,再通过刷题,应该能提高一些自己的水平。
一般动态规划的时间复杂度=状态的数量*转移的计算量
背包模型
背包类问题大概就是给你一个容量有限的背包、一些有一定价值并会占用一定体积的物品,问你能得到的最大价值,根据问题约束条件的不同,大致分为下面几种。
01背包
例题:AcWing2
顾名思义,01背包问题中,一个物品要么用0次,要么用一次。
动态规划问题我们一般从两方面来思考:状态表示+状态转移。
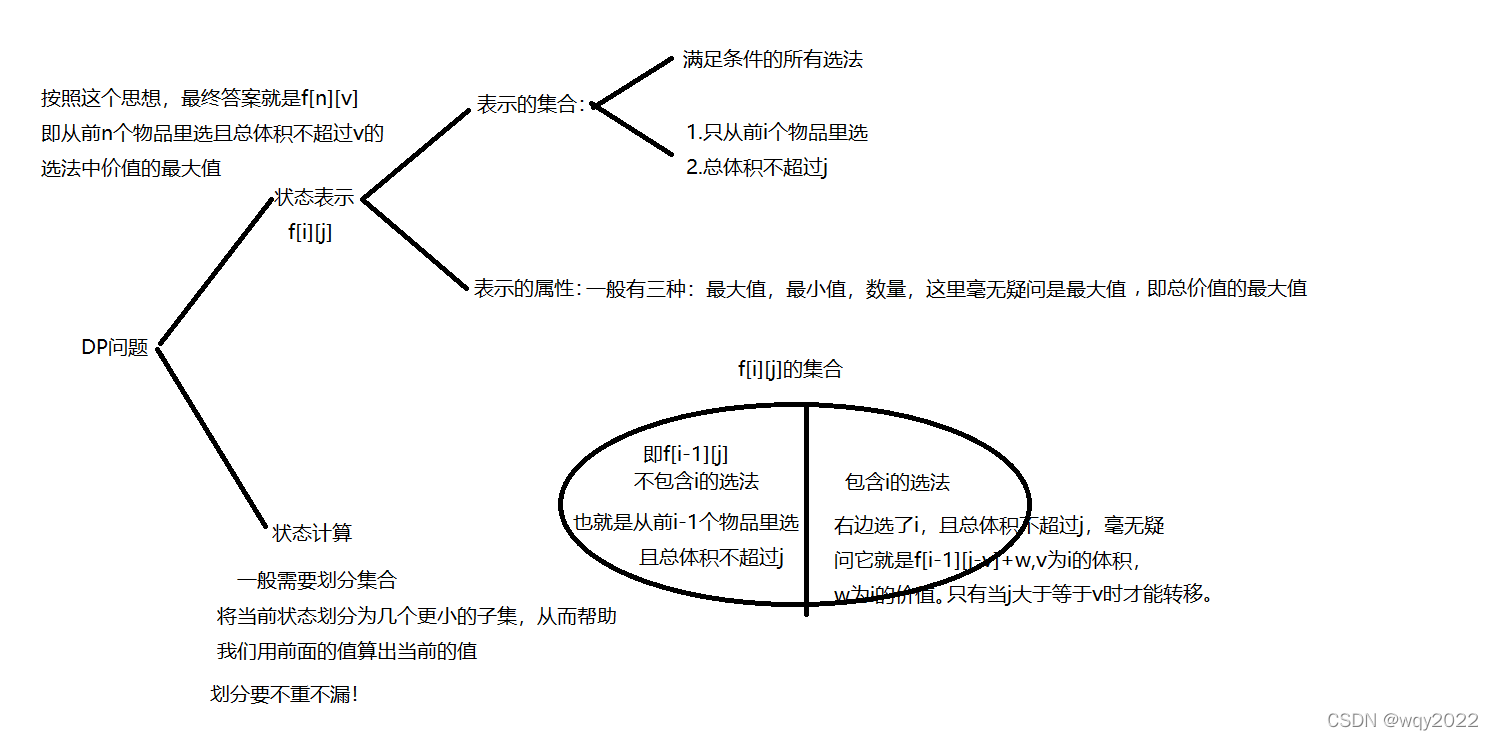
因此f[i][j]=max(f[i-1][j],f[i-1][j-v]+w);
另外,我们要注意dp问题中要考虑基础情况,假设m为背包总体积,本题中f[0][0~m]表示考虑0件物品,那么最终一定都是0,在本题中虽然不考虑这种情况不会出错(全局变量默认为0),但有的题中不考虑基础情况是很可能出错的。
代码实现:
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // 各个物品的体积
int w[N]; // 各个物品的价值
int f[N][N]; // f[i][j], j体积下只考虑前i个物品的最大价值
int main() {
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
// 当前背包容量装不进第i个物品,则价值等于只考虑前i-1个物品的情况
if(j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
通过观察,我们在算第i个物品时,只用到了i-1个物品的各个属性,因此我们可以用滚动数组优化:
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int v[N]; // 各个物品的体积
int w[N]; // 各个物品的价值
int f[2][N]; // f[i][j], j体积下只考虑前i个物品的最大价值
int main() {
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++){
// 当前背包容量装不进第i个物品,则价值等于只考虑前i-1个物品的情况
if(j < v[i])
f[i & 1][j] = f[i - 1 & 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i & 1][j] = max(f[i - 1 & 1][j], f[i - 1 & 1][j - v[i]] + w[i]);
}
cout << f[n & 1][m] << endl;
return 0;
}
再观察,我们算第i件物品时只用到了考虑i-1件物品时的属性,而且我们算j体积下的情况时用到的是上一层j-v体积下的价值,因此我们只用一维数组,然后让体积从大到小循环就可以了。体积若还是从小到大循环,算j体积时用到的就是当前层的j-v体积,就不对了。
代码实现:
#include<iostream>
using namespace std;
const int N=1e3+10;
int w[N],v[N];
int f[N];
int main(){
int n,s;
cin>>n>>s;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=s;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[s]<<endl;
return 0;
}
完全背包
例题:AcWing3
完全背包问题和01背包问题很像,但每个物品可以使用无限次
我们依然按照上面的思考方式。
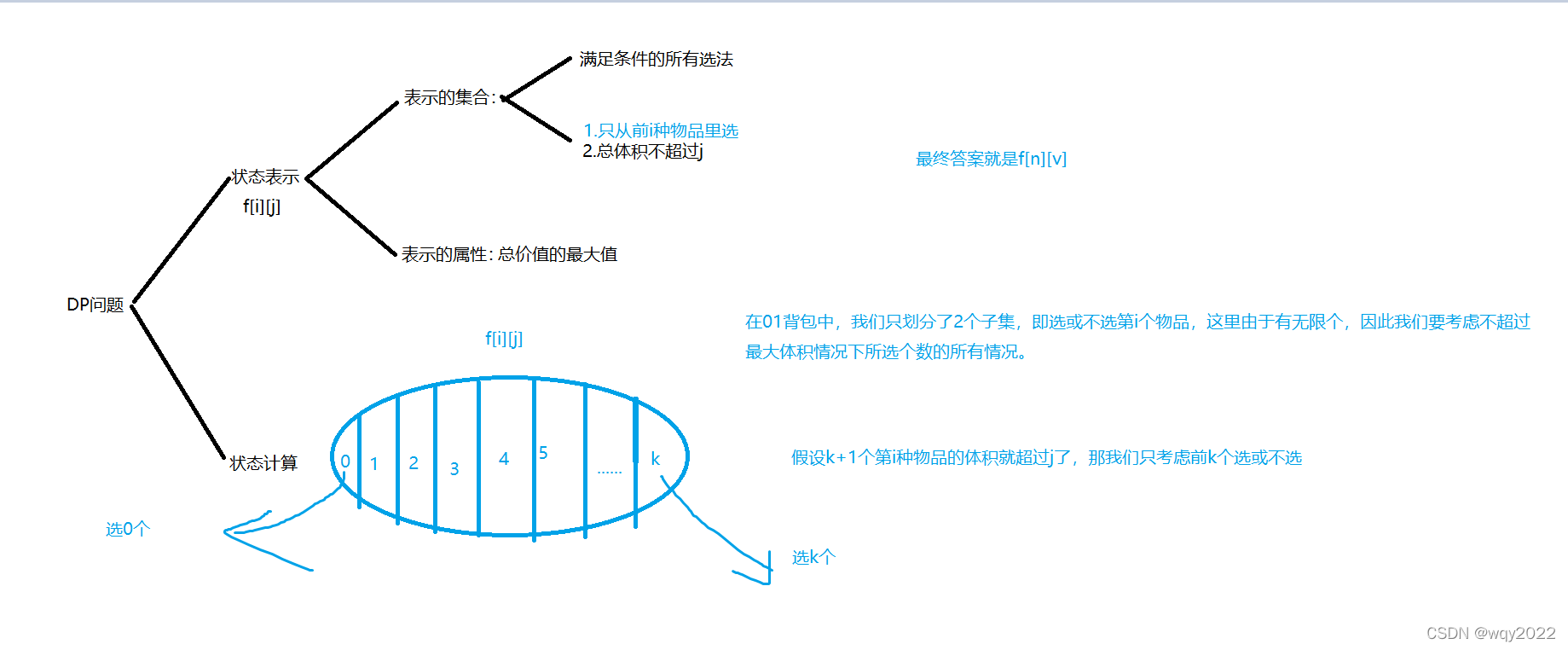
那么f[i][j]=max(f[i-1][j-x* v]+x *w),x=0,1,2…k;
这样我们的朴素代码就能写出来了:
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N],w[N];
int main(){
int n,m;
cin>>n>>m;
for(int i = 1 ; i <= n ;i ++){
cin>>v[i]>>w[i];
}
for(int i = 1 ; i<=n ;i++){//考虑前i种物品
for(int j = 0 ; j<=m ;j++){//考虑所有体积
for(int k = 0 ; k*v[i]<=j ; k++)//考虑选k个物品
f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
cout<<f[n][m]<<endl;
}
毫无疑问,这个三重循环的时间复杂度是会tle的,因此我们考虑优化。
我们发现:
f[i][j]=max(f[i-1][j-x* v]+x w),x=0,1,2…k;
f[i][j-v]=max(f[i-1][j-x v]+x *w),x=1,2…k;
因此f[i][j]=max(f[i-1][j],f[i][j-v]+w);
然后我们发现我们的空间也可以优化一维,因为我们推出最终的状态转移方程种只用到了上一层同一体积的价值和当前层更小体积的价值,最终代码:
#include<iostream>
using namespace std;
int n,s;
const int N=1010;
int v[N],w[N];
int f[N];
int main(){
cin>>n>>s;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
for(int i=1;i<=n;i++){
for(int j=v[i];j<=s;j++){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[s]<<endl;
return 0;
}
多重背包1
例题:AcWing4
多重背包问题中每种物品的数量是有限个,你可能感觉:这不是变简单了吗?其实是更复杂了,不过我们会在后面感受到这种复杂,因为本题数据范围并不大。分析图:
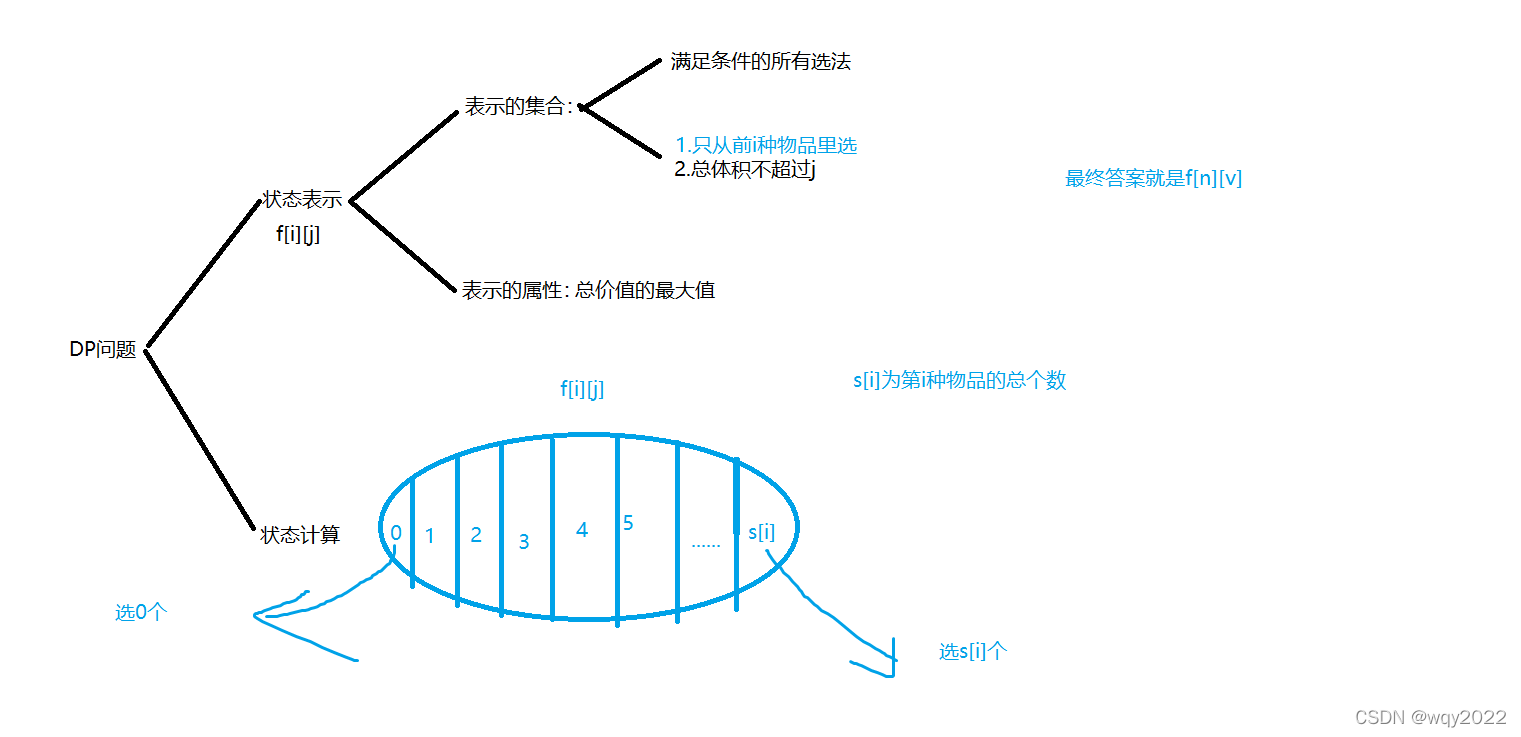
我们发现,这不就是完全背包的朴素版本吗?
代码实现:
#include<iostream>
using namespace std;
int n,m;
const int N=110;
int v[N],w[N],s[N];//s表示各种物品的数量
int f[N][N];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];
for(int i=1;i<=n;i++){//考虑前i种物品
for(int j=1;j<=m;j++){//体积为0的肯定是0,就不管了
for(int k=0;k<=s[i]&&k*v[i]<=j;k++){//最多有s[i]个且体积不能超
f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
}
}
}
cout<<f[n][m]<<endl;
return 0;
}
这里我们还是可以滚动数组优化的,就不赘述了。但是我们并不能采用和上一题一样的优化,原因:

和完全背包相比,f[i][j-v]的最后多了一项,这样就不能用完全背包的优化方法了,但是我们发现我们可以减去一个偏移量然后用滑动窗口优化,具体会在多重背包3里(先鸽着 等我的动态规划提高出来吧,估计要好久。。。)
多重背包2
例题:AcWing4
本题数据范围较大,用上面的做法铁定超时,因此我们考虑优化,我们想到,第i种物品都可以选0~s[i]次,那我们用二进制优化,把多个第i种物品压为1个并保证可以让它被选0 ~s[i]次,那我们的时间复杂度就会变为O(nvlog s),就能过掉了,举个例子,假如说第1种物品可以选16个,那么我们把1个该物品当成一个物品,2个该物品当成一个物品,4个该物品当成一个物品,8个物品当成一个物品,剩下的一个物品当成一个物品,这样我们任意组合,也就是把一个数分为2的次方数,该次方从0开始,一直递增,不能分的时候剩下的单独分为一个,最终就能得到任意个数该物品的组合,接下来我们直接做01背包就行了。
代码实现:
#include<iostream>
using namespace std;
int n,m;
const int N=12010,M=2010;//每种物品最多有2000个,最多划分为11个物品,这里为了保险算12个,因此N为12*1000
int v[N],w[N];
int f[M];
int main(){
cin>>n>>m;
int cnt=0;
for(int i=1;i<=n;i++){
int a,b,s;
cin>>a>>b>>s;
int k=1;
while(k<=s){
cnt++;
v[cnt]=a*k;
w[cnt]=b*k;
s-=k;
k*=2;
}
if(s){
cnt++;
v[cnt]=s*a;
w[cnt]=s*b;
}
}
n=cnt;
for(int i=1;i<=n;i++){//01背包
for(int j=m;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m]<<endl;
return 0;
}
分组背包
例题:AcWing9
本题种有多组物品,而且每组物品内物品的v,w可能不同,每组物品中最多只能选一个物品,其实和前面的问题大同小异。
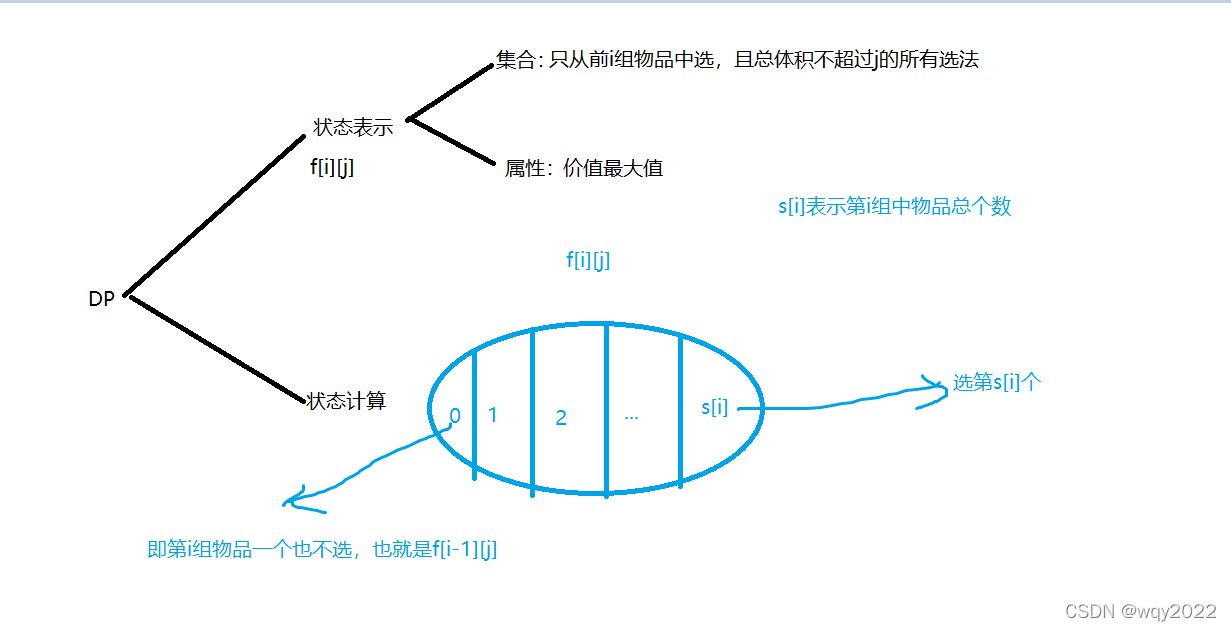
这里同样可以优化成一维,我就直接写一维的了
代码实现:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i ++ ){
cin >> s[i];
for (int j = 0; j < s[i]; j ++ )
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= 1; j -- )//这里不能先枚举k再枚举j,因为那样会在枚举下一个物品时上一个物品已经导致f数组前面的被改变,就不能优化成一维了,但如果只用滚动数组优化或者不优化空间的话,先枚举k和先枚举j都是可以的
for (int k = 0; k < s[i]; k ++ )
if (v[i][k] <= j)
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}
线性DP
顾名思义,线性的DP,主要指状态转移方程的线性,比如说一行一行挨个算,思考起来应该比较简单(但愿如此吧。。。)
数字三角形
很经典的一题。例题:AcWing898
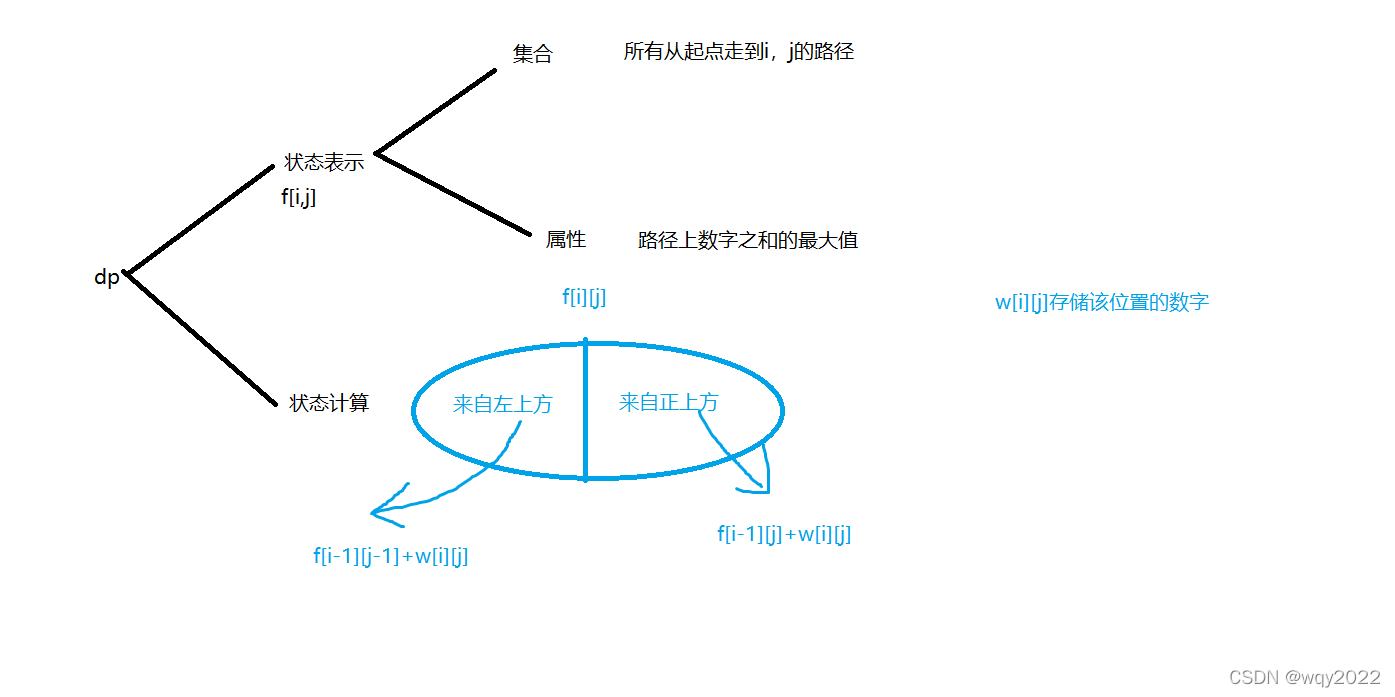
不过需要注意,该题中存在负数,因此我们先把数组全部初始化为一个很小的值,这里有一个技巧,用memset(dp,128,sizeof 128)即可初始化为一个很小的负数。另外,考虑到dp[1][1]由dp[0][0]和dp[0][1]转移而来,把这两个数初始化为0。
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
int n;
const int N=510;
int a[N][N];//即图中的w数组
int dp[N][N];//即图中的f数组
int main(){
cin>>n;
memset(dp,128,sizeof(dp));
dp[0][1]=dp[0][0]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){
cin>>a[i][j];
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];
}
}
int res=-1e9;
for(int i=1;i<=n;i++) res=max(res,dp[n][i]);
cout<<res<<endl;
return 0;
}
最长上升子序列1
也是一道非常经典的问题,例题:AcWing895
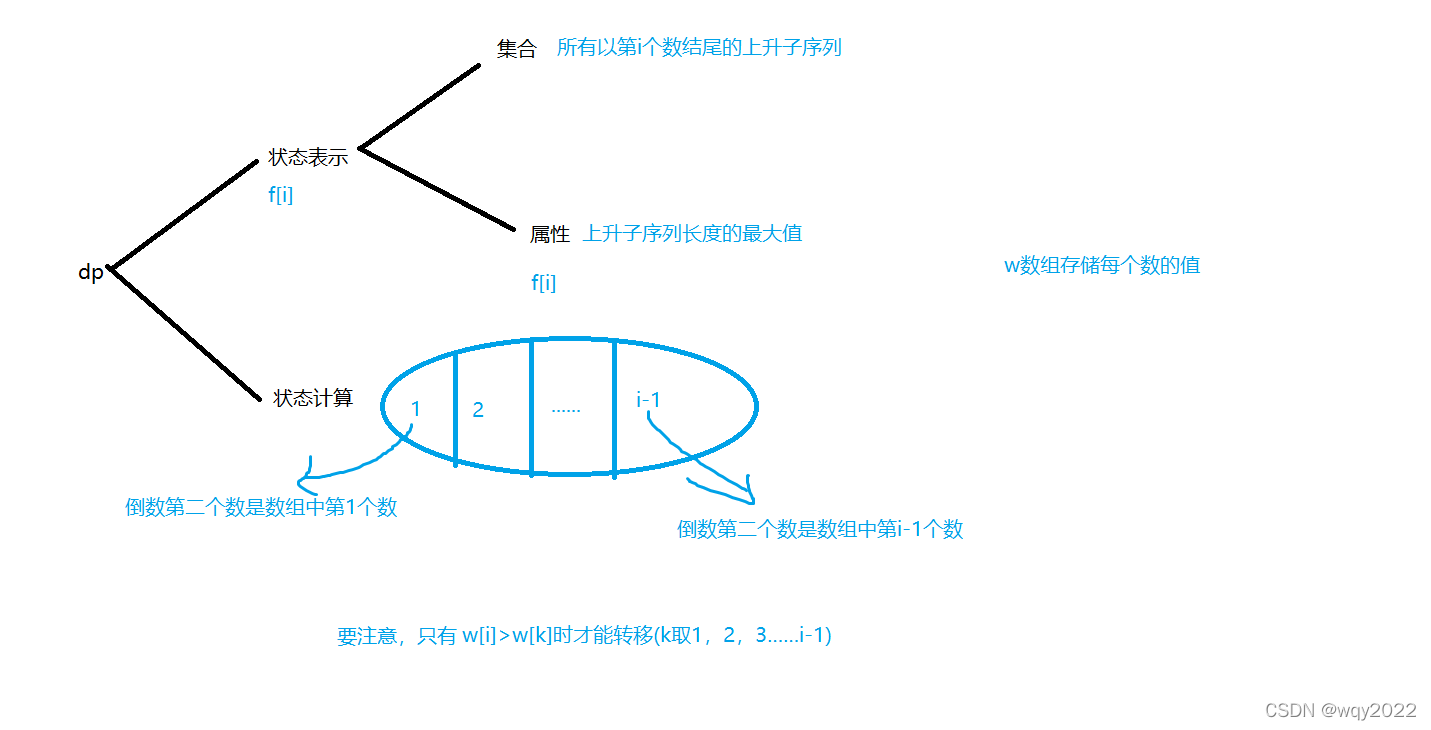
另外,如果可以转移,f[i]可以看作以第j个数结尾的上升子序列长度+1。(j即为选择的数的次序)
代码实现:
#include<iostream>
using namespace std;
int n;
const int N=1e4+10;
int a[N];
int f[N];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",a+i);
for(int i=1;i<=n;i++){
f[i]=1;//最少也是1,即只有a[i]的情况
for(int j=1;j<i;j++){//枚举第1~i-1个数作为倒数第二个数
if(a[j]<a[i]){//只有上升时才能转移
f[i]=max(f[i],f[j]+1);
}
}
}
int res=0;//记录最大值
for(int i=1;i<=n;i++) res=max(res,f[i]);//找出最长的
printf("%d",res);
return 0;
}
如果我们想要记录一下最长的那个序列,只需多开一个数组,在代码上稍加修改就可以了。
#include<iostream>
using namespace std;
int n;
const int N=1e4+10;
int a[N];
int f[N];
int g[N];//g[i]表示以i结尾的序列前一个数的下标
void print(int k){
if(k==0){//k为0,说明递归完毕
return ;
}
print(g[k]);//递归到最后一层
printf("%d ",a[k]);//打印
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",a+i);
for(int i=1;i<=n;i++){
f[i]=1;
g[i]=0;//序列只有一个数,前一个数为0
for(int j=1;j<i;j++){
if(a[j]<a[i]){
if(f[i]<f[j]+1){
f[i]=f[j]+1;
g[i]=j;//以i结尾序列的前一个数的下标是j
}
}
}
}
int res=1;//res记录最大值的下标
for(int i=1;i<=n;i++){
if(f[i]>f[res]){
res=i;
}
}
printf("%d\n",f[res]);//输出最大值
print(res);//递归打印,因为我们如果正常打印的话就是倒序的,因此递归打印
return 0;
}
最长上升子序列2
例题:AcWing896
这道题的数据范围比较大,上种方法肯定是不行的,要考虑优化。
我们通过上升子序列的长度分类,对于每个长度的上升子序列,我们只记录结尾值最小的那一个(更有上升空间)。类似一种贪心的思想。我们可以得到,长度为6的序列结尾的值一定大于长度为5的序列结尾的值(仔细想想,可以用反推的思想)。这样我们枚举每一个a[i]时,就把它接到最大的小于a[i]的结尾后面,可以分为两种情况,如果a[i]大于最长的序列的结尾值,就把a[i]加到结尾,否则就找到第一个大于等于a[i]的值改为a[i]。
超easy代码实现:
时间复杂度O(n*log n)
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
int n;
vector<int> ans;
int main(){
scanf("%d",&n);
int tmp;
scanf("%d",&tmp);
ans.push_back(tmp);//直接先放进去一个
for(int i=1;i<n;i++){
scanf("%d",&tmp);
if(tmp>ans.back()) ans.push_back(tmp);
else *(lower_bound(ans.begin(),ans.end(),tmp))=tmp;
}
printf("%d",ans.size());//大小即为最长长度
return 0;
}
最长公共子序列
例题:AcWing897
这题的集合划分其实还是有点东西的。
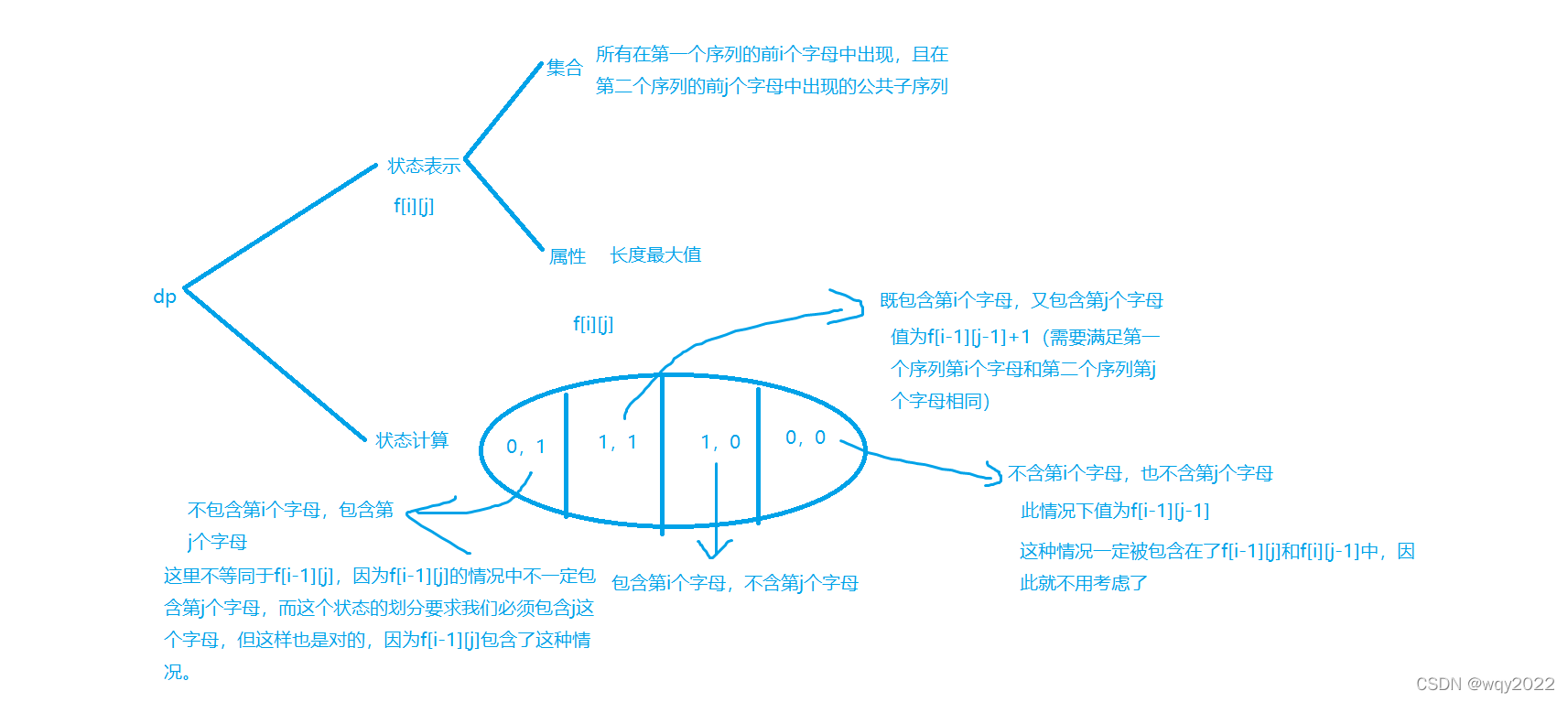
#include<iostream>//代码很easy...
using namespace std;
const int N=1010;
int n,m;
char a[N],b[N];
int f[N][N];
int main(){
scanf("%d%d%s%s",&n,&m,a+1,b+1);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
printf("%d",f[n][m]);
return 0;
}
区间DP
区间DP我感觉还是有模板可循的,但我还是菜,不会写
例题:AcWing282
注意!这里只能合并相邻的两堆石子,因此不是哈夫曼树的贪心。
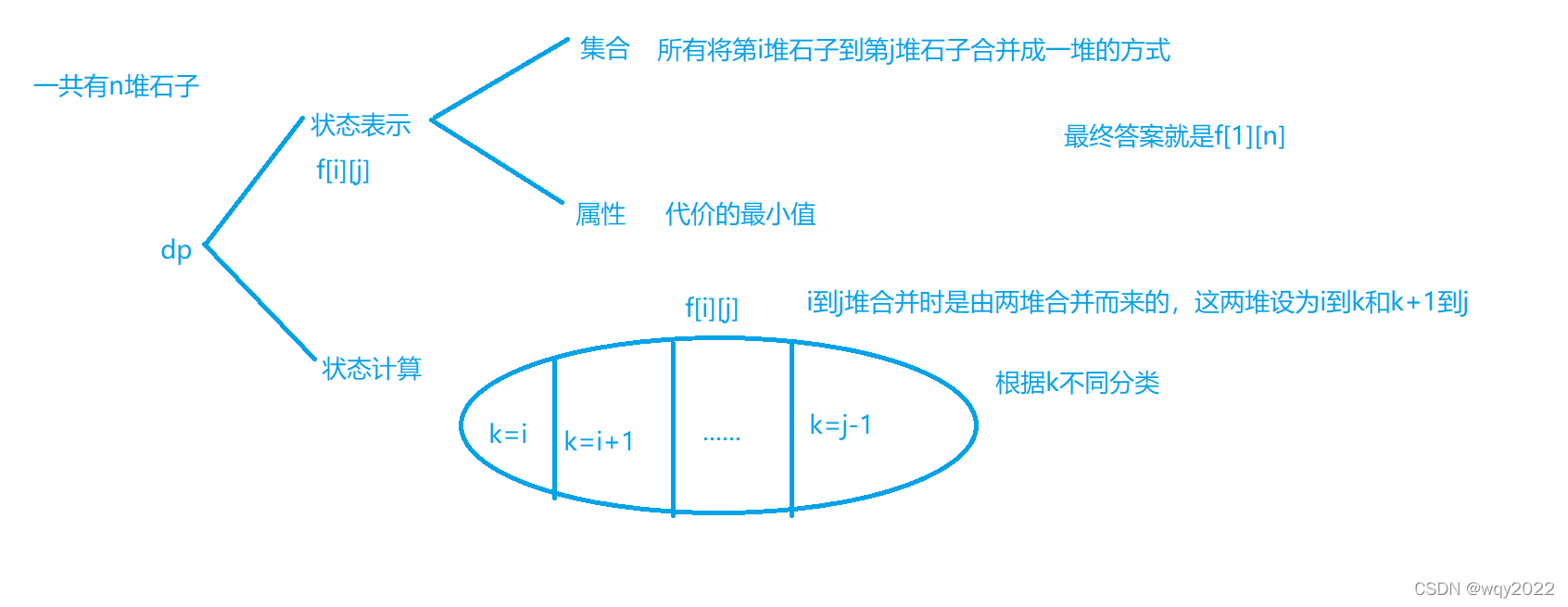
所以f[i][j]=min(f[i][k]+f[k+1][j]+i到j所有石子的总重量(用前缀和求))k可以取i~j-1
我们先枚举区间长度,再枚举区间的起点,再枚举分界点(区间dp一般都是这样的),根据状态转移方程就能递推出答案了,区间长度为1时是不需要合并的,不用枚举了。
代码实现:
#include<iostream>
using namespace std;
int n;
const int N=310;
int s[N];
int dp[N][N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i];
s[i]+=s[i-1];
}
for(int len=2;len<=n;len++){//长度为1的代价就是0,不用管了
for(int i=1;i+len-1<=n;i++){//右边界<=n
int j=i+len-1;
dp[i][j]=1e9;//先初始化为较大值,然后迭代求出最小值
for(int k=i;k<j;k++){
dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+s[j]-s[i-1]);
}
}
}
cout<<dp[1][n];
return 0;
}
状态压缩DP
状态压缩dp一般有棋盘类和别的种类,我感觉非常难,主要使用2进制来表示状态然后进行状态转移。
一般看到题目的数据范围很小,就可以考虑是否用状态压缩了。
棋盘类
例题1:AcWing291
非常经典的一题。
要我们求所有摆放的方案数,我们发现,只要我们把所有横着的摆完,那竖着的就只能填充下去了(注意要特判是否可行),因此我们只求横着摆放的合法的方案数就可以了。其实判断是否合法还是比较简单的,我们只需枚举每一列,判断每一个列连续空着的方格数,如果位偶数个,那就是合法的。
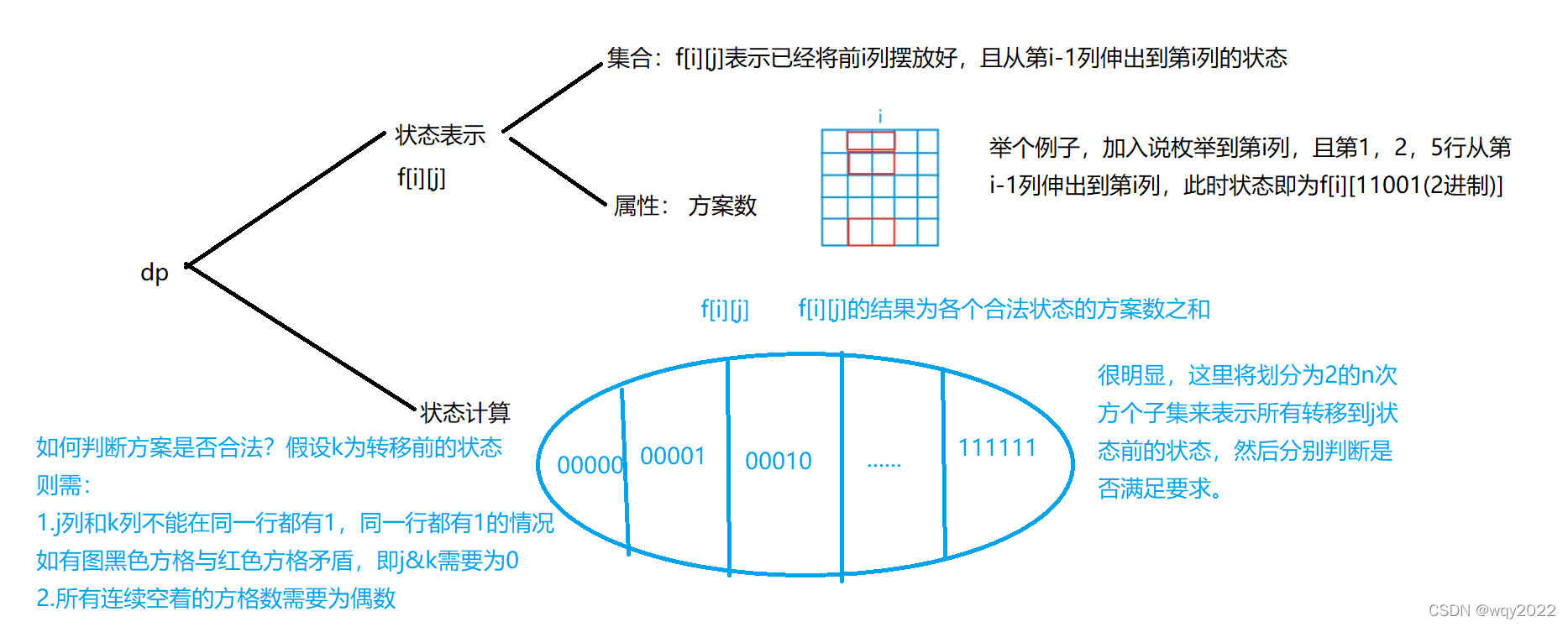
另外一提,这道题我们也可以把状态转移的过程看作是i-1行竖着的被掰直了,也是比较好理解的。
另外这道题的最终答案是f[m][0],假设一共有m列,下标从0开始,f[m][0]就表示0~m-1列已经摆好,且第m-1列没有方格伸到m列的方案数,就是正好摆满0 ~m-1列的方案数。本题最多会运算11*211*211次,又由于有多组测试数据,不加优化是可能tle的,因此我们可以先预处理出来对于每一个状态,所有能转移到它的状态,再预处理出来每一个状态是否满足连续空着的方格数都是偶数个,再只用这些状态循环并判断。
代码实现:
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
int n,m;//n为行,m为列
const int N=12,M=1<<N;//因为我们要算0~11行,所以N开到12
typedef long long LL;
LL dp[N][M];
vector<int> state[M];
bool st[M];
int main(){
while(cin>>n>>m,n|m){
int cnt;
memset(dp,0,sizeof dp);
for(int i=0;i<1<<n;i++){
st[i]=true;
cnt=0;
for(int j=0;j<n;j++){
if(i>>j&1){//如果遇到1
if(cnt&1){//判断一下前面0的个数
st[i]=false;//为奇数的话此状态不合要求
}
cnt=0;//清空
}
else cnt++;//否则cnt++
}
if(cnt&1) st[i]=false;//判断最后一组空格(如果有的话
}
for(int i=0;i<1<<n;i++){//枚举一列的所有状态
state[i].clear();
for(int j=0;j<1<<n;j++){//找出能转移到i的状态j
if((i&j)==0&&st[i|j]){//i,j不能同时有一行横着摆,并且j转移到i后需满足连续空格数为偶数
state[i].push_back(j);
}
}
}
dp[0][0]=1;//初始化,第0行摆放只能全竖着摆放,就一种方案,这里即使第一列只有奇数个也没关系,都能正确转移
for(int i=1;i<=m;i++){//算到m列,更好输出
for(int j=0;j<1<<n;j++){//枚举所有状态
for(auto k:state[j]){//遍历能转移到j状态的状态
dp[i][j]+=dp[i-1][k];
}
}
}
cout<<dp[m][0]<<endl;
}
return 0;
}
集合类
例题:AcWing91
非常经典的一题。俗称旅行商问题。
有没有感觉到这道题很熟悉?没错,这就是去年蓝桥杯省赛A组填空最后一题(差不多)!
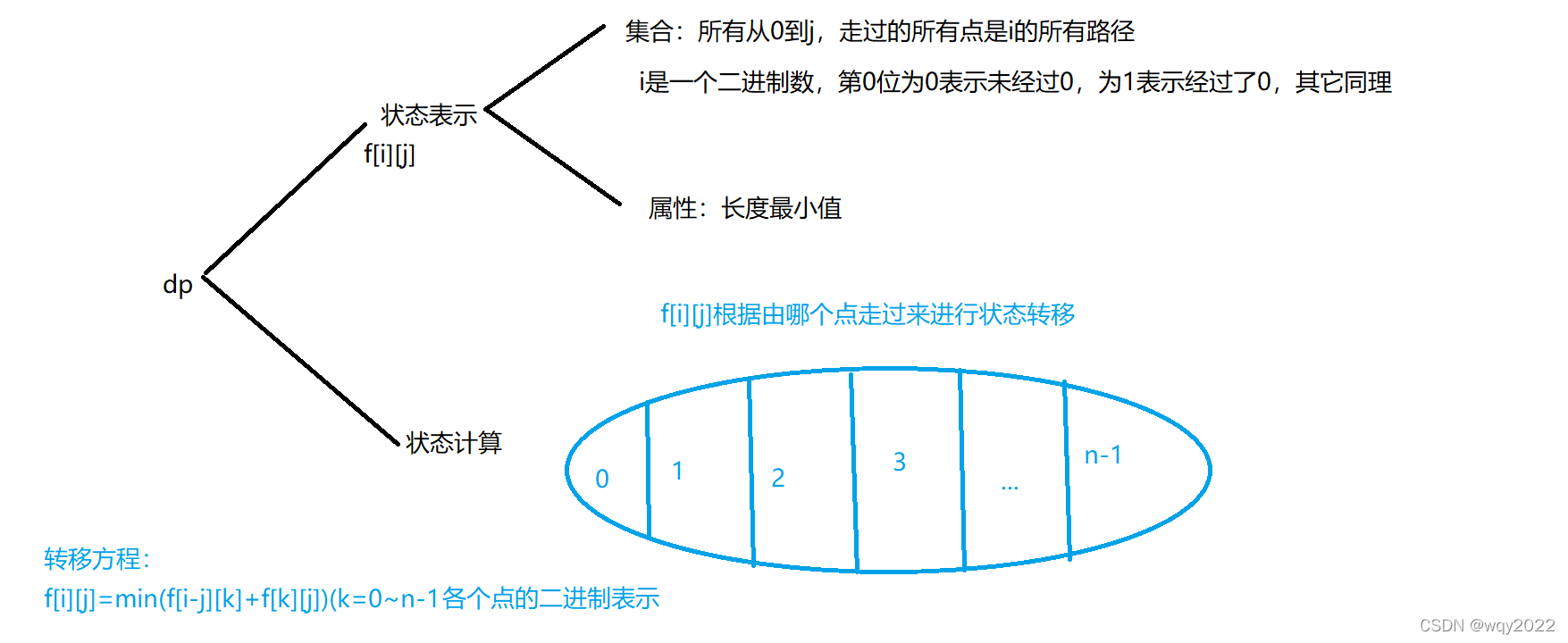
代码实现:
#include<iostream>
#include<cstring>
using namespace std;
const int N=20,M=1<<N;
int n;
int d[N][N];
int f[M][N];
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d",&d[i][j]);
}
}
memset(f,0x3f,sizeof f);//初始化为正无穷
f[1][0]=0;//从0走到0且经过0点(把从右往左数第一个数看作第0位,第0位为1,说明经过了0点)的距离为0
for(int i=0;i<1<<n;i++){//枚举所有经过路径的状态
for(int j=0;j<n;j++){//枚举走到的终点
if(i>>j&1){//只有当i表示的状态包含了j这个点
for(int k=0;k<n;k++){//枚举中转的站点
if((i-(1<<j))>>k&1){//i去点j这个点后如果还包含了k这个点,就更新
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+d[k][j]);
//如果走过除去j之外的i状态所包含的所有点且落点在k的距离与从k到j的距离之和小于f[i][j]就更新
}
}
}
}
}
cout<<f[(1<<n)-1][n-1]<<endl;//最终结果是走遍所有点且落脚点在n-1的答案
return 0;
}
树形DP
例题:AcWing285 这题异常真实
这题其实也是一个状态机模型,等我动态规划提高就写它 。
直接看这题可能会毫无头绪,不知道怎么表示和转移状态,其实我们只需要分类讨论就可以了。
我们用f[i][0]表示第i个人不去参加舞会时以他为根的子树中所有人happy值之和的最大值
f[i][1]表示第i个人去参加舞会时以他为根的子树中所有人happy值之和的最大值
代码实现:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 6010;
int n;
int h[N], e[N], ne[N], idx;//链式前向星存储树
int happy[N];//每个人的happy值
int f[N][2];//状态
bool has_fa[N];//记录每个点有没有父节点
void add(int a, int b){
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u){
f[u][1] = happy[u];
for (int i = h[u]; ~i; i = ne[i]){//~i等同于i!=-1
int j = e[i];
dfs(j);//先算出来子树的状态
f[u][1] += f[j][0];//当前人去,他的儿子就不能去
f[u][0] += max(f[j][0], f[j][1]);//否则儿子可去可不去
}
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &happy[i]);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ ){
int a, b;
scanf("%d%d", &a, &b);
add(b, a);
has_fa[a] = true;
}
int root = 1;
while (has_fa[root]) root ++ ;//找到根节点(即无父结点的点)
dfs(root);
printf("%d\n", max(f[root][0], f[root][1]));//最大值为二者之一
return 0;
}
数位DP
数位dp也基本都有章可循,难度一般不高于小学数奥(我是废物),基本上是分类讨论的思想。
例题:AcWing338
求a到b之间各个数字出现的次数,可以用1~b种各个数字出现的次数减去1 ~a-1种各个数字出现的次数,我们遇到的很多数位dp都是这种思想。
我们直接实现一个函数cnt(n,x)来求0或者1~n中x出现的次数,再往下求就很easy了,所以重点成了cnt函数的实现。
画图分类:

代码实现:
#include<iostream>
#include<vector>
using namespace std;
int a,b;
int get(vector<int> num,int l,int r){
int res=0;
for(int i=l;i>=r;i--){
res=res*10+num[i];
}
return res;
}
int pow10(int x){
int res=1;
while(x--){
res*=10;
}
return res;
}
int cnt(int n,int x){
if(!n) return 0;//如果n是0,就直接返回0
vector<int> num;//num存储n的每一位
while(n){
num.push_back(n%10);
n/=10;
}
n=num.size();//废物再利用,记录位数
int res=0;
//从最高位开始枚举
for(int i=n-1-!x;i>=0;i--){//如果统计0的个数,就不能把0放在最高位(设为n-1位,最低位是第0位),因为如果n-1位是0,其实整个数字是没有n-1位的
if(i<n-1){//不是最高位才有这种情况
//get函数求出由n-1位到第i+1位数字组成的一个整数
//pow函数求出10的i次方
res+=get(num,n-1,i+1)*pow10(i);
if(!x) res-=pow10(i);//如果是0的话减去10的i次方
}
if(num[i]==x){//如果相等,加上后面所有位组成的数+1
res+=get(num,i-1,0)+1;
}
else if(num[i]>x){//否则加上10的i次方
res+=pow10(i);
}
}
return res;
}
int main(){
while(cin>>a>>b,a|b){
if(a>b)swap(a,b);
for(int i=0;i<10;i++){
cout<<cnt(b,i)-cnt(a-1,i)<<" ";
}
puts("");
}
return 0;
}
其实可以发现,好像并不难,但把所有情况分清楚也是比较困难的。
记忆化搜索
例题:AcWing901
一看题目我们就能想到搜索,但是如果我们对每一个点都爆搜,肯定会tle,我们发现我们在搜一些点的时候已经更新了别的点的答案,因此利用这一点,我们能完成记忆化搜索。
代码实现:
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 310;
int n, m;
int g[N][N];//g数组记录答案,-1时表示没搜过
int f[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int dp(int x, int y){
int &v = f[x][y];
if (v != -1) return v;//搜过直接返回
v = 1;//初始化为1
for (int i = 0; i < 4; i ++ ){//四个方向
int a = x + dx[i], b = y + dy[i];
if (a >= 1 && a <= n && b >= 1 && b <= m && g[x][y] > g[a][b])//要满足题意
v = max(v, dp(a, b) + 1);//更新
}
return v;
}
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &g[i][j]);
memset(f, -1, sizeof f);
int res = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
res = max(res, dp(i, j));
printf("%d\n", res);
return 0;
}
计数类DP
例题:AcWing900
这不就是完全背包问题求方案数吗,把1~n中每个数字k都看成一种占用k体积的物品,每种物品都可以无限使用,求恰好达到n体积的所有选法。
重拳出击:
#include <iostream>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main(){
cin >> n;
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
cout << f[n] << endl;
return 0;
}
DP快把我学死了 ,学习DP真爽!