直接插入排序
基本思想
对于单趟排序:把待排序的值插入到已经排好序的序列中。待排序的值逐一与序列中的值比较,直到找到自己的位置。
全趟排序:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。
- 举一个单趟排序的例子
2 4 8 9 10
假设我们需要将5插入到上面的升序序列中:
1、首先5与10进行比较,10比5大,那么就将10向后移动一个位置。
2 4 8 9 10
2、然后再与9进行比较大小,9比5大,跟上面一样,9向后移动一个位置。
2 4 8 9 10
3、同理,8也比5大
2 4 8 9 10
4、4比5小。此时将5插入到序列中
2 4 5 8 9 10
此时,单趟插入排序就已经结束了
那么如果我们要对一个无序的序列进行排序,我们可以从序列中的第二个数开始,重复单趟排序的过程
参考代码
#include <stdio.h>
//升序
void InsertSort(int* arr, int n)
{
int i = 0;
//序列长度为n时,要进行n-1次单趟排序
for (i = 0; i < n - 1; i++)
{
int end = i;
int x = arr[end + 1];
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = x;
}
}
int main()
{
int arr[] = { 1,6,5,4,9,10,2 };
InsertSort(arr, sizeof(arr) / sizeof(arr[0]));
int i = 0;
for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}
直接插入排序特性总结
- 元素集合越接近有序,直接插入排序算法的时间效率越高。
- 时间复杂度:O(N^2)
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
希尔排序
基本思想
从前面的插入排序中我们可以了解到,如果一个序列越接近有序序列,那么对此序列进行直接插入排序,时间复杂度就越接近O(n)。希尔排序简单来说,就是想在对序列进行排序时,先设法让序列接近有序,然后再进行插入排序,那么时间复杂度就可以接近O(n).
想要让序列变成一个接近有序的序列。我们可以让序列进行分组(用gap表示),分别对gap组序列进行插入排序。称为预排序。

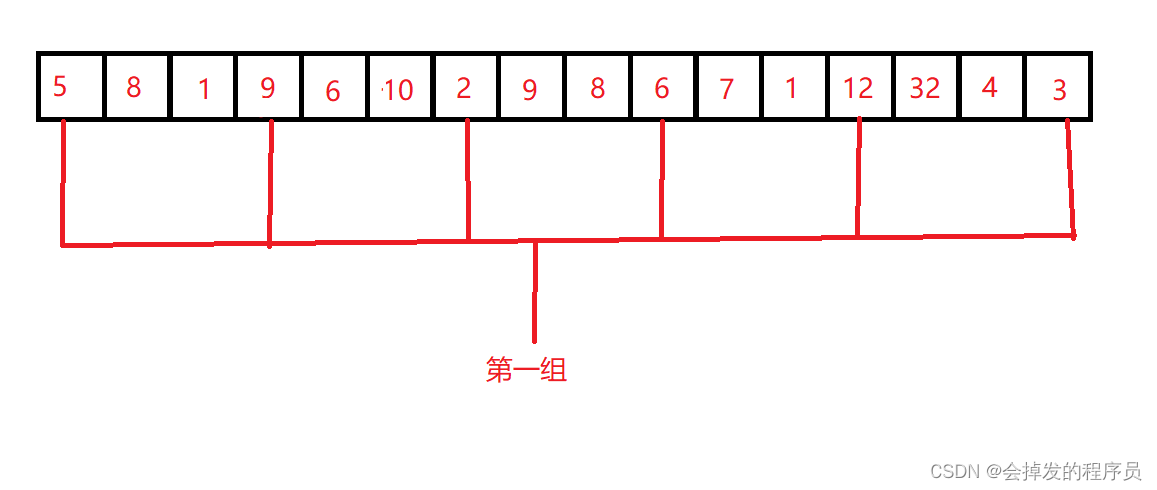
对上面的序列进行预排序,假设gap=3(分为三组),每隔两个数就取一个。
第一组:
5 9 2 6 12 3
对第一组进行插入排序后
2 3 5 6 9 12
此时整体序列为

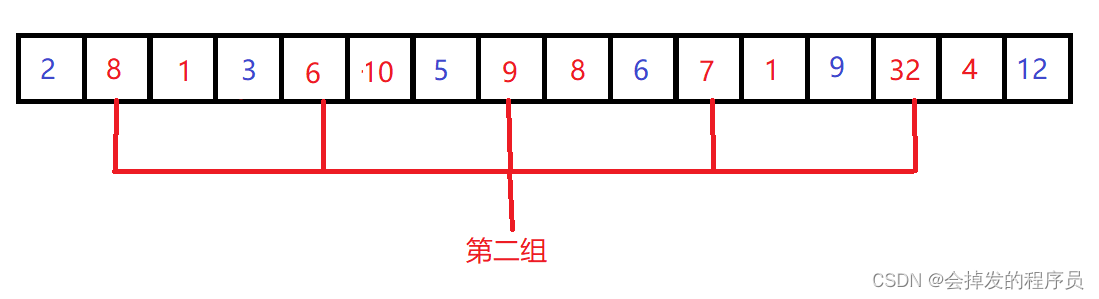
第二组:
8 6 9 7 32
对第二组进行插入排序后
6 7 8 9 32
此时整体序列为

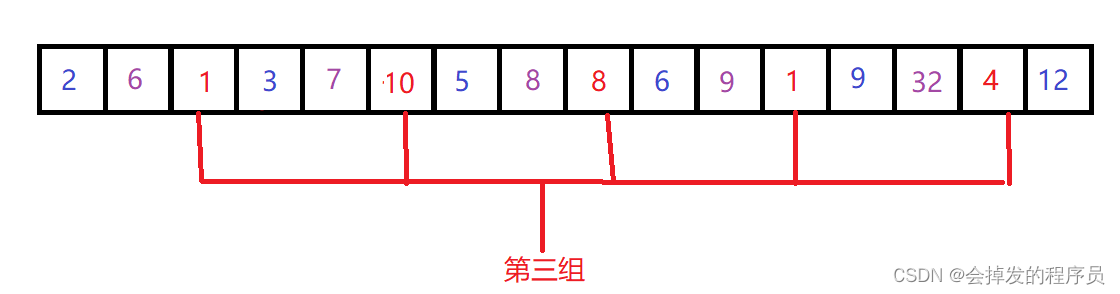
第三组:
1 10 8 1 4
对第三组进行插入排序后
1 1 4 8 10
此时整体序列为

此时的序列相对于开始是更接近有序的,这样对整体进行插入排序,效率上会提高很多。
在真正排序中,gap值的选取是至关重要的,特别是当数据非常庞大时。因此,为了避免这种麻烦,我们可以将gap的值(假设序列长度为n)从n/3+1或者n/2开始。一直递减到1为止。
参考代码
#include <stdio.h>
//gap越大,预排越快,预排后越不接近有序
//gap越小,预排越慢,预排后越接近有序
//gap==1,就是插入排序
//升序
void ShellSort(int* arr, int n)
{
int gap = n;
//多组与排序(gap > 1)+ 直接插入排序(gap == 1)
while (gap > 1)
{
//gap /= 2;
gap = gap / 3 + 1;
int i = 0;
for (i = 0; i < n - gap; i++)
{
int end = i;
int x = arr[end + gap];
while (end >= 0)
{
if (arr[end] > x)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = x;
}
}
}
int main()
{
int arr[] = { 5,6,4,1,2,3,7,10,15,12,2,4,5,6,7,0,6,3,32,7,8,100 };
ShellSort(arr, sizeof(arr) / sizeof(arr[0]));
int i = 0;
for (i = 0; i < sizeof(arr) / sizeof(arr[0]); i++)
{
printf("%d ", arr[i]);
}
return 0;
}