图
图是由有穷非空集合的顶点和顶点之间的边组成的集合,通常表示为G(V,E),其中G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
在线性结构中,每个元素都只有一个直接前驱和直接后继,?要用来表示一对一的数据结构;在树形结构中,数据之间有着明显的父子关系,每个数据和其子节点的多个数据相关,?要用来表示一对多的数据结构;在图形结构中,数据之间具有任意关系,图中任意两个数据元素之间都可能相关,可用来表示多对多的数据结构。图根据边
的属性可分为无向图和有向图。
无向图与有向图
无向图
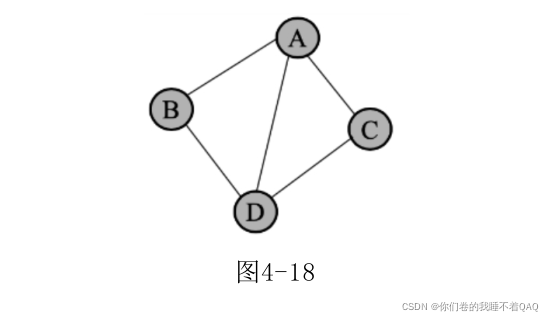
有向图:
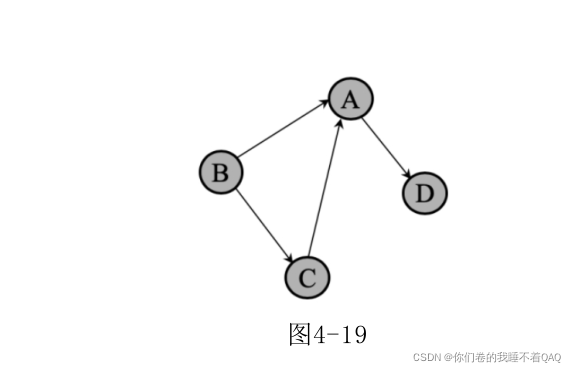
邻接矩阵
我们有了图,但是在计算机里,怎么表示他们呢?
这里用到了一种邻接矩阵的方式:
无向图邻接矩阵如:
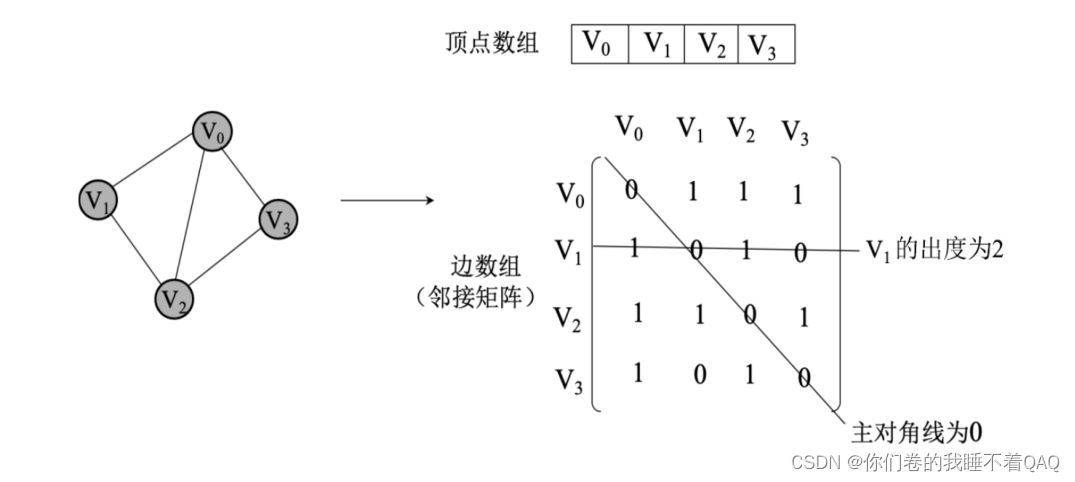
某一点到某一点的距离矩阵的数值表示;其中主对角线为o,因为自己到自己的距离肯定是0。
横向看某点,可以看出度。比如上图中的v1这一行有两个1,证明有两条边从v1点出去。
出度表示该点在网络中的能力,出度高的结点一般都是关键节点。
有向图邻接矩阵:
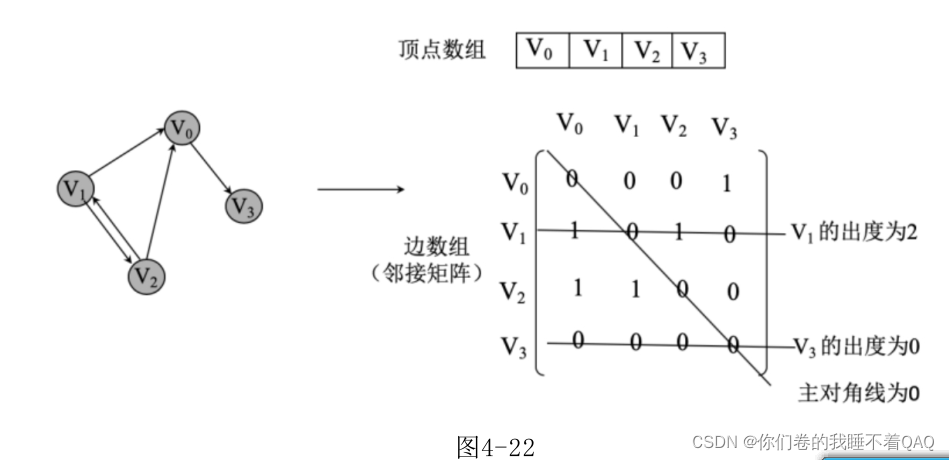
带权重的邻接矩阵:
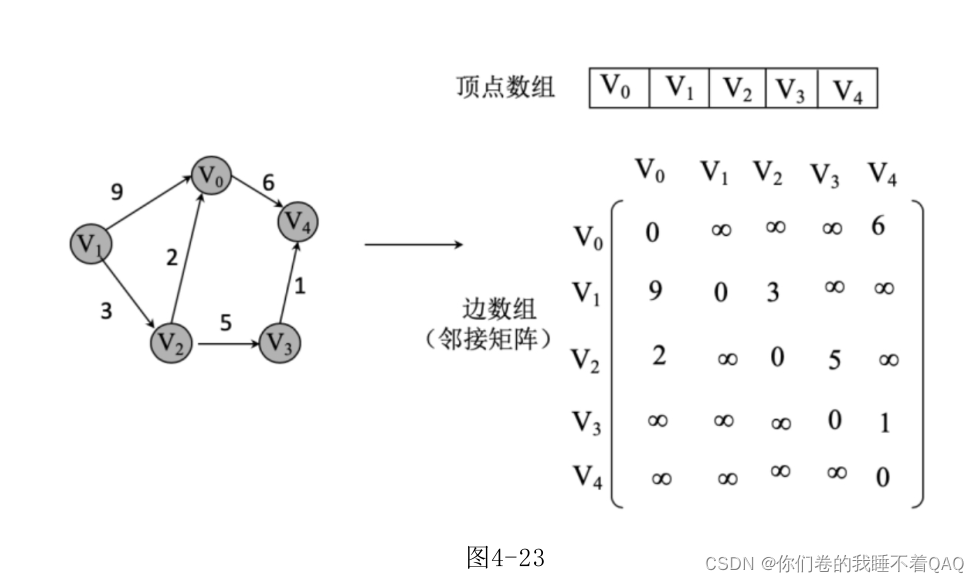
邻接表
有了邻接矩阵,我们发现,大部分点都是0,没有什么作用。而且矩阵在计算机中占据大量内存
因此为了优化数据结构,发明出邻接表。(利用链表进行实现)
无向图邻接表
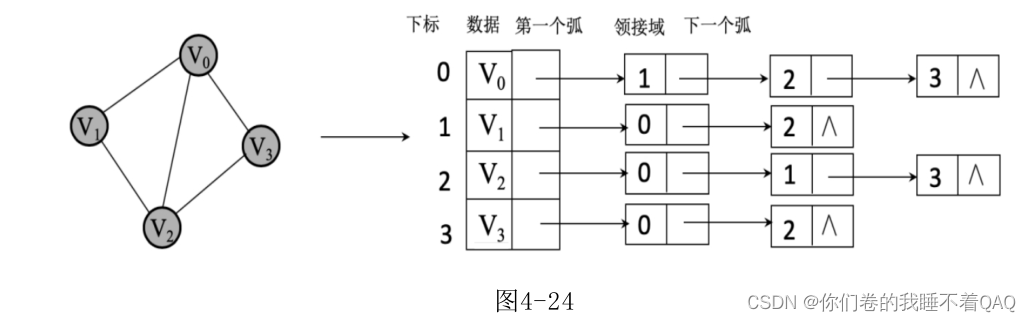
邻接表 是一个节点的相邻节点与之连接
比如v0 ;v0点有三个相邻节点(v1 v2 v3),那么链表就是 v0-v1-v2-v3
依次类似
有向图邻接表:
如果有权重,那么在链表节点增加一块数据域用于储存权值。
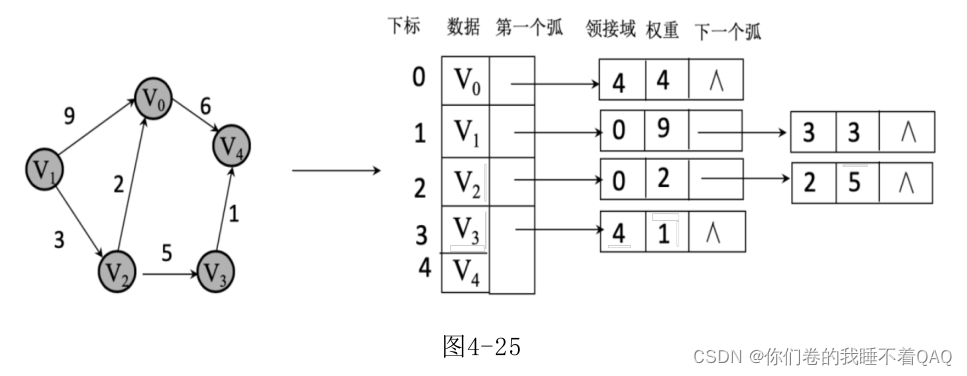
图的遍历
图的遍历与树的遍历差不多,分为广度优先和深度优先
通俗的说就是“雨露均沾”与“一条道走到黑”。
图的广度优先遍历如下:
广度优先遍历也叫作广度优先搜索(Breadth First Search),
类似于树的分层遍历算法,其定义为:假设从图中某个顶点V出发,在
访问了V之后依次访问V的各个未曾访问过的邻接点,然后分别从这些
邻接点出发依次访问它们的邻接点,并使先被访问的顶点的邻接点先
于后被访问的顶点的邻接点被访问,直到图中所有已被访问的顶点的
邻接点都被访问;若此时图中尚有顶点未被访问,则另选图中未曾被
访问的一个顶点作为起始点重复上述过程,直至图中所有顶点均被访
问。
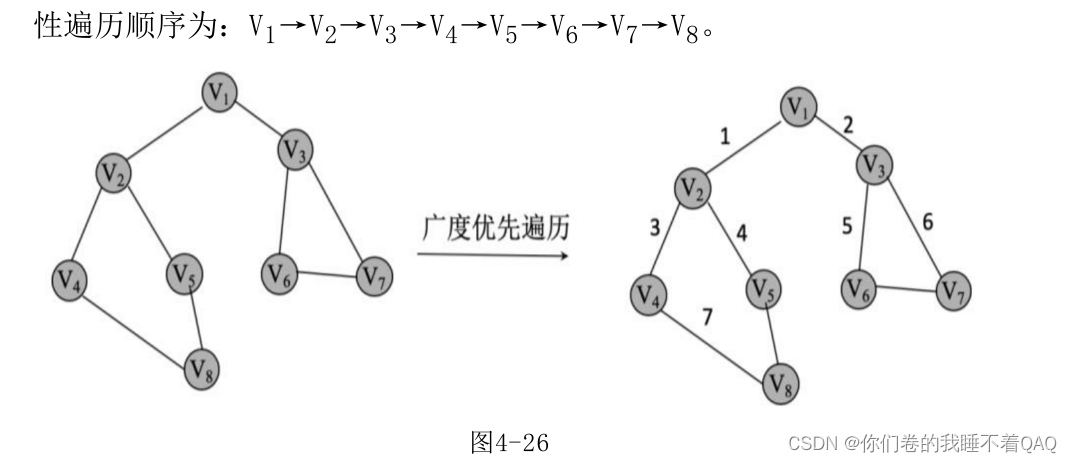
假设从起始点V 1 开始遍历,首先访问V 1 和V 1 的邻接点V 2 和V 3 ,然后依次访问V 2 的邻接点V 4 和
V 5 ,及V 3 的邻接点V 6 和V 7 ,最后访问V 4 的邻接点V 8 ,于是得到节点的线性遍历顺序为:V 1 →V 2 →V 3 →V 4 →V 5 →V 6 →V 7 →V 8 。
图的深度优先遍历如下:
图 的 深 度 优 先 遍 历 也 叫 作 深 度 优 先 搜 索 ( Depth First
Search),类似于树的先根遍历(先访问树的根节点)。其定义如
下:
假设从图中的某个顶点V出发,在访问V节点后依次从V未被访问的
邻接点出发以深度优先的原则遍历图,直到图中所有和V节点路径连通
的顶点都被访问;若此时图中尚有顶点未被访问,则另选一个未曾访
问的顶点作为起始点重复上述过程,直至图中所有节点都被访问。
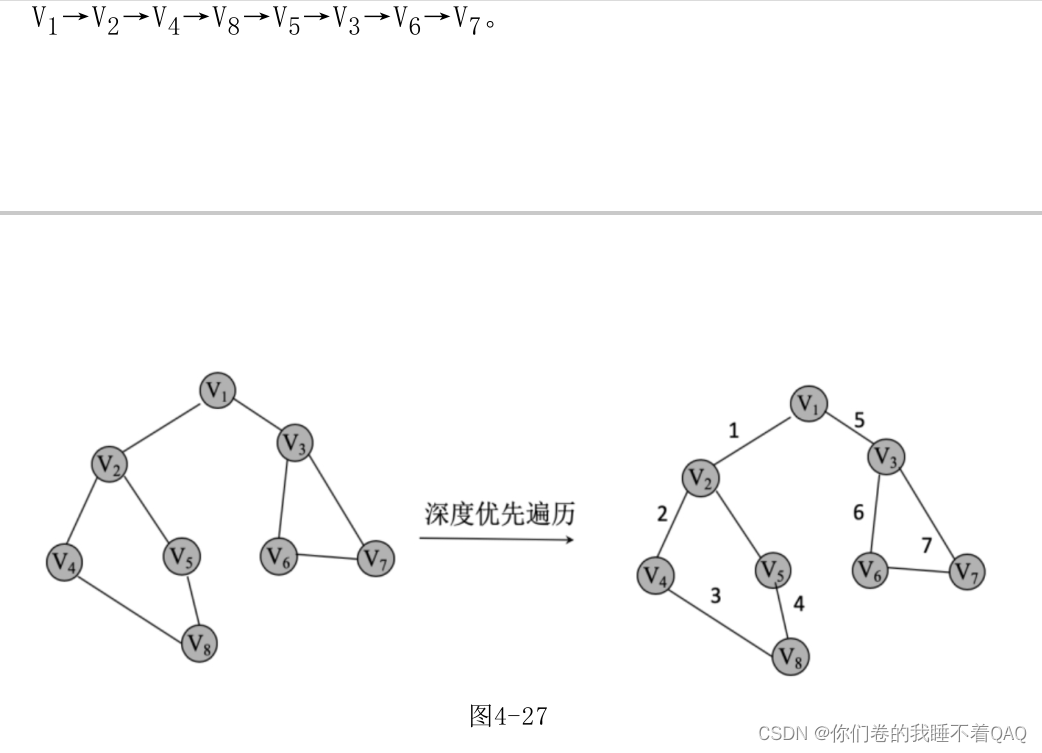
假设从起始点V 1 开始遍历,在访问了V 1 后选择其邻接点V 2 。因为V 2 未曾被访问,所以从V 2 出发进行深度优先遍历。依此类推,接着从V 4 、V 8 、V 5 出发进行遍历。在访问了V 5 后,由于V 5 的邻接点都被访问过,则遍历回退到V 8 。同理,继续回退到V 4 、V 2 直至V 1 ,此时V 1 的另一个邻接点V 3 未被访问,则遍历操作又 从 V 1 到 V 3 继 续 进 行 下 去 , 得 到 节 点 的 线 性 顺 序 为 :V 1 →V 2 →V 4 →V 8 →V 5 →V 3 →V 6 →V 7 。