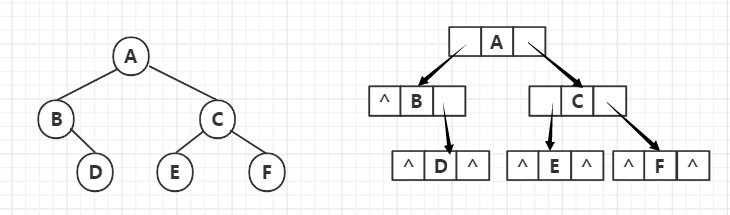
（一）二叉树的存储结构

?二叉树在计算机中具有顺序存储和链式存储两种存储方式。在本文所讨论的算法中，二叉树均是采用二叉链表的存储方式

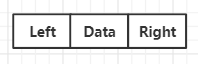
struct Node{
    Node *Left;
    Node *Right;
    char Data;
};

其中Left用来保存指向该节点左儿子的指针，Right用来保存指向该节点右儿子的指针?

（二）二叉树的遍历

在学习创建二叉树之前，我们不妨先学习二叉树的遍历，因为二叉树的创建可以借助二叉树的遍历算法完成

先根（中根、后根、层次）遍历二叉树得到的结点序列，称为先根序（中根、后根、层次）列

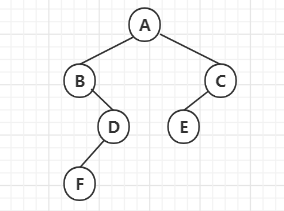
例如，对于下图所示的二叉树，其

先根序列为ABDFCE
中根序列为BFDAEC
后根序列为FDBECA
层次序列为ABCDEF

1.先根遍历

步骤为：①访问根、②遍历左子树、③遍历右子树

先根遍历递归算法

/*先根遍历*/
void preOrder(Node * root){
    //递归出口
    if(root==nullptr)
        return;

    //访问根
    cout<<root->data;
    //遍历左子树
    preOrder(root->left);
    //遍历右子树
    preOrder(root->right);
}

先根遍历非递归算法

#include <iostream>
using namespace std;

struct Node{
    Node *left;
    Node *right;
    char data;
    Node():left(nullptr),right(nullptr),data('#'){}
};

//栈
class Stack{
public:
    Stack():top(0){
        for(int i=0;i<s_size;i++){
            s[i]=nullptr;
        }
    }
    //入栈
    void push(Node *p){
        if(top<s_size){
            s[top]=p;
            top++;
        }else{
            cout<<"Stack overflow!"<<endl;
            return;
        }
    }
    //出栈
    Node *pop(){
        if(top==0){
            return nullptr;
        }else{
            top--;
            return s[top];
        }
    }
    bool isEmpty(){
        if(top==0)
            return true;
        else
            return false;
    }
private:
    const int s_size=20;
    Node *s[20];
    int top;
};

/*先根遍历非递归算法*/
void nPreOrder(Node * root){
    if(root == nullptr){
        return;
    }
    Stack s;
    Node *p=root;
    //根节点入栈
    s.push(p);
    //栈不为空时:
    while(!s.isEmpty()){
        //弹栈:
        p=s.pop();
        cout<<p->data;
        //右儿子入栈:
        if(p->right!=nullptr){
            s.push(p->right);
        }
        //左儿子入栈:
        if(p->left!=nullptr){
            s.push(p->left);
        }
    }
    return;
}

/*创建二叉树*/
Node * createTree(char t[20],int *num){
    char ch=t[(*num)];
    (*num)++;
    if(ch=='#'){
        return nullptr;
    }
    //创建根结点
    Node *p=new Node();
    p->data=ch;
    //创建左子树
    p->left=createTree(t,num);
    //创建右子树
    p->right=createTree(t,num);
    return p;
}

int main()
{
    char t[20]="AB#DF###CE###";
    int i=0;//计数器
    Node *root=nullptr;

    root=createTree(t,&i);
    nPreOrder(root);
    return 0;
}

2.中根遍历

步骤为：①遍历左子树、②访问根、③遍历右子树

中根遍历递归算法

/*中根遍历*/
void inOrder(Node * root){
    //递归出口
    if(root==nullptr)
        return;

    //遍历左子树
    inOrder(root->left);
    //访问根
    cout<<root->data;
    //遍历右子树
    inOrder(root->right);
}

中根遍历非递归算法

/*中根遍历非递归算法*/
void nInOrder(Node * root){
    if(root==nullptr){
        return;
    }
    Stack s;
    Node *p=root;

    while( (!s.isEmpty()) || (p!=nullptr) ){
        while(p!=nullptr){
            s.push(p);
            p=p->left;
        }
        p=s.pop();
        cout<<p->data;
        p=p->right;
    }
}

3.后根遍历

步骤为：①遍历左子树、②遍历右子树、③访问根

后根遍历递归算法

/*后根遍历*/
void postOrder(Node * root){
    //递归出口
    if(root==nullptr)
        return;

    //遍历左子树
    postOrder(root->left);
    //遍历右子树
    postOrder(root->right);
    //访问根
    cout<<root->data;
}

后根遍历非递归算法

//栈2元素的结构
struct NodeOfStack{
    Node *pnode;
    int times;//入栈次数
    NodeOfStack():pnode(nullptr),times(0){}
};
//栈2
class Stack2{
public:
    Stack2():top(0){
        for(int i=0;i<s_size;i++){
            s[i].pnode=nullptr;
            s[i].times=0;
        }
    }
    //入栈
    void push(Node *p,int t){
        if(top<s_size){
            s[top].pnode=p;
            s[top].times=t;
            top++;
        }else{
            cout<<"Stack overflow!"<<endl;
            return;
        }
    }
    //出栈
    NodeOfStack pop(){
        if(top>0){
            top--;
            return s[top];
        }
    }
    bool isEmpty(){
        if(top==0)
            return true;
        else
            return false;
    }
private:
    const int s_size=20;
    NodeOfStack s[20];
    int top;
};

/*后根遍历非递归算法*/
void nPostOrder(Node * root){
    if(root==nullptr){
        return;
    }
    Stack2 s;
    s.push(root,0);
    while(!s.isEmpty()){
        NodeOfStack nos=s.pop();//中间变量，存储每一次栈弹出的数据
        Node *p=nos.pnode;
        if(nos.times==0){
            s.push(nos.pnode,1);
            if(p->left!=nullptr){
                s.push(p->left,0);
            }
        }else if(nos.times==1){
            s.push(nos.pnode,2);
            if(p->right!=nullptr){
                s.push(p->right,0);
            }
        }else if(nos.times==2){
            cout<<p->data;
        }
    }
}

4.层次遍历

层次遍历即按照二叉树的层数从小到大，同一层中从左到右的顺序访问二叉树的所有结点

//队列
class Queue{
public:
    Queue():font(-1),rear(0),q_count(0){
        for(int i=0;i<q_size;i++){
            q[i]=nullptr;
        }
    }
    //入队
    void qIn(Node *p){
        if(q_count>=q_size){
            //队列满了
            cout<<"Queue overflow!"<<endl;
            return;
        }
        if(q_count==0){
            //队列为空
            font=rear;
        }
        q[rear]=p;
        rear=(rear+1)%q_size;
        q_count++;
    }
    //出队
    Node *qOut(){
        if(q_count==0){
            //队列为空
            return nullptr;
        }
        Node *p=q[font];
        font=(font+1)%q_size;
        q_count--;
        return p;
    }
    int q_count;//队列中的元素个数
private:
    const int q_size=20;//队列大小
    Node *q[20];//q在逻辑上是一个环状队列
    int font;//队列的头部，也是将要出队的元素的位置
    int rear;//下一个元素入队的位置
};

/*层次遍历*/
void levelOrder(Node * root){
    if(root==nullptr){
        return;
    }
    Queue q;
    q.qIn(root);//入队
    while(q.q_count>0){
        Node *p=q.qOut();
        cout<<p->data;
        if(p->left!=nullptr){
            q.qIn(p->left);
        }
        if(p->right!=nullptr){
            q.qIn(p->right);
        }
    }
}

（三）二叉树的创建

前面我们说了，二叉树的创建可以借助二叉树遍历算法的思想来完成，现在我们先思考一个问题——只根据先根序列，能唯一确定一棵二叉树吗？

显然是不能的。为了解决这个问题，我们在先根序列中加入一些特殊的符号（比如'#'）来表示空指针的位置，例如对于下图所示的二叉树，其先根序列为ABDFCE，改造后的序列为AB#DF###CE###

#include <iostream>
using namespace std;

struct Node{
    Node *left;
    Node *right;
    char data;
    Node():left(nullptr),right(nullptr),data('#'){}
};

/*创建二叉树*/
Node * createTree(char t[20],int *num){
    char ch=t[(*num)];
    (*num)++;
    if(ch=='#'){
        return nullptr;
    }
    //创建根结点
    Node *p=new Node();
    p->data=ch;
    //创建左子树
    p->left=createTree(t,num);
    //创建右子树
    p->right=createTree(t,num);
    return p;
}

int main()
{
    char t[20]="AB#DF###CE###";
    int i=0;//计数器
    Node *root=nullptr;

    root=createTree(t,&i);
    return 0;
}