算法思想

ISAP算法的主要基础是BFS去搜索“去权值”的最短增广路，从源点到汇点的分层查找，总能找到最短路径，每次找到当前到达汇点的最短路径（这里的最短路径是相对于层数的），之后沿着当前的最短路径进行增流，然后重新开始

求得最短增广路的思路有很多，在ISAP中，采用“贴标签”的方法：标记所有节点到汇点的最短距离，通过BFS，将汇点的标签设置为0，邻接点的标签为1，以此类推，贴好标签之后，从源点开始沿着标签递减且有可行邻接边的方向前进，然后找到增广路之后增流，在当前节点无法前进时，重贴标签

算法步骤

标签，设置好每个节点的最短距离
找增广路，当源点的标签值≥总节点数时，转向5，否则沿着标签值递增的且有可行邻接边的方向前进，到达汇点，转向3，无法前进，转向4
增流，在混合网络中沿增广路同边增，反边减
重贴标签，当前节点无法前进时，若拥有当前节点标签值的只有该节点一个，转向5，否则更新当前节点标签值为所有可行邻接点标签值最小值+1，若无可行邻接边，则令当前节点标签值等于节点数，回溯一步，转向2
找到最大流

关于优化

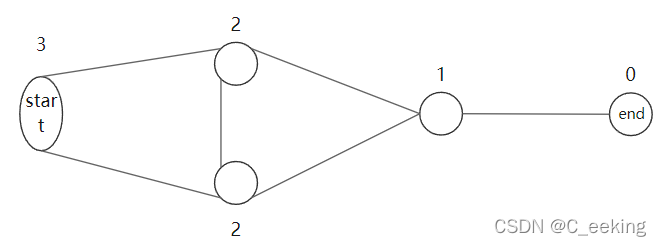
算法步骤中在当前节点无法前进时，假设当前节点为 $u$ ，无法前进说明 $u$ 与 $e n d$ 之间已经没有连通性了，此时按道理来说应该回溯更新，但是，如果此时 $u$ 的标签值唯一，即如图所示的情况，由于每次都是走的最短路，所以其余所有点的标签值都大于 $u$ ，因此其余任意一个点若想到达 $e n d$ ，都必须经过 $u$ ，而因为 $u$ 已经不与 $e n d$ 连通，所以没有其他的点能够再到达 $e n d$ ，因此无更多的增广路，到此，程序可以直接终止

在这里插入图片描述
代码

struct node {
    int next,to,cap,flow;//链式前向星，容量和流
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;//注意是从0开始存的
}
void BFS(int t,int n) {//标初始高度
    queue<int>q;
    memset(h,-1,sizeof(h));//初始化高度
    memset(g,0,sizeof(g));//初始化计数
    h[t]=0;//汇点高度默认为0
    q.push(t);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        g[h[u]]++;//统计高度为h[u]的节点数
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(h[v]==-1) {
                h[v]=h[u]+1;
                q.push(v);
            }
        }
    }
}
int ISAP(int s,int t,int n) {//源点，汇点，点数(包括源点汇点，传入值应该为题设节点数+2)
    BFS(t,n);
    int res=0,u=s,d=inf;
    while(h[s]<n) { //整个图变成一条链，包括源点汇点
        int i=head[u];
        if(u==s)d=inf;//特判源点
        for(; ~i; i=e[i].next) { //BFS
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&h[u]==h[v]+1) {
                u=v;//更换当前点
                pre[v]=i;//记录前一条边便于增流
                d=min(d,e[i].cap-e[i].flow);//获得最小可增量
                if(u==t) {
                    while(u!=s) {
                        int j=pre[u];
                        e[j].flow+=d;
                        e[j^1].flow-=d;//增流
                        u=e[j^1].to;//回溯
                    }
                    res+=d;//累和最大流
                    d=inf;//初始化
                }
                break;
            }
        }
        if(i==-1) {//无法前进
            if(--g[h[u]]==0)break;//优化
            int hmin=n-1;//初始化
            for(int i=head[u]; ~i; i=e[i].next)//BFS
                if(e[i].cap>e[i].flow)//可行邻接点
                    hmin=min(hmin,h[e[i].to]);
            h[u]=hmin+1;
            g[h[u]]++;//对应高度计数+1
            if(u!=s)u=e[pre[u]^1].to;//继续回溯
        }
    }
    return res;
}

训练

POJ3281

题目大意：一个农场，有n头牛，每头对食物和饮品有特定的某些喜好，现在有F种食物和D种饮品，每头牛只会按照自己的喜好选择（也就是不属于喜好的不会要），一种食物/饮品只会匹配一头牛，求出同时获得食物和饮品的牛最多有多少头

思路：题目的意思很简单，但一开始读找不到解决问题的模型，分析一下，题目为求解多约束的最大值问题，可以考虑使用网络流模型，如果按照源点-食物-牛-饮品-汇点来构造网络，可以满足食物与饮品一一对应牛，但是无法满足牛一一对应食物和饮品，因此可以将牛拆成两个点，点之间用权值为1的边连接
建图方面也需要打量好，源点编号为0，汇点编号为 $f + 2 \times n + d + 1$ (食物，牛×2，饮品)，源点与食物连边，cap=1，牛到牛的拆点连边，cap=1，饮品到汇点连边，cap=1，具体可见代码

代码

#include <iostream>
#include <queue>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e3;
int head[maxn],g[maxn],cnt,h[maxn],pre[maxn];
int f,d,n,s,t;
struct node {
    int next,to,cap,flow;//链式前向星，容量和流
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;//注意是从0开始存的
}
void BFS(int t,int n) {//标初始高度
    queue<int>q;
    memset(h,-1,sizeof(h));//初始化高度
    memset(g,0,sizeof(g));//初始化计数
    h[t]=0;//汇点高度默认为0
    q.push(t);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        g[h[u]]++;//统计高度为h[u]的节点数
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(h[v]==-1) {
                h[v]=h[u]+1;
                q.push(v);
            }
        }
    }
}
int ISAP(int s,int t,int n) {//源点，汇点，点数
    BFS(t,n);
    int res=0,u=s,d=inf;
    while(h[s]<n) { //整个图变成一条链
        int i=head[u];
        if(u==s)d=inf;//特判源点
        for(; ~i; i=e[i].next) { //BFS
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&h[u]==h[v]+1) {
                u=v;//更换当前点
                pre[v]=i;//记录前一条边便于增流
                d=min(d,e[i].cap-e[i].flow);//获得最小可增量
                if(u==t) {
                    while(u!=s) {
                        int j=pre[u];
                        e[j].flow+=d;
                        e[j^1].flow-=d;//增流
                        u=e[j^1].to;//回溯
                    }
                    res+=d;//累和最大流
                    d=inf;//初始化
                }
                break;
            }
        }
        if(i==-1) {//无法前进
            if(--g[h[u]]==0)break;//优化
            int hmin=n-1;//初始化
            for(int i=head[u]; ~i; i=e[i].next)//BFS
                if(e[i].cap>e[i].flow)//可行邻接点
                    hmin=min(hmin,h[e[i].to]);
            h[u]=hmin+1;
            g[h[u]]++;//对应高度计数+1
            if(u!=s)u=e[pre[u]^1].to;//继续回溯
        }
    }
    return res;
}
int main() {
    scanf("%d%d%d",&n,&f,&d);
    memset(head,-1,sizeof(head));
    memset(pre,-1,sizeof(pre));
    s=0,t=f+2*n+d+1;
    for(int i=1; i<=f; i++) {
        Add(0,i,1,0);
        Add(i,0,0,0);
    }
    for(int i=f+2*n+1; i<=f+2*n+d; i++) {
        Add(i,t,1,0);
        Add(t,i,0,0);
    }
    for(int i=f+1; i<=f+n; i++) {
        Add(i,i+n,1,0);
        Add(i+n,i,0,0);
    }
    for(int i=1; i<=n; i++) {
        int x,y;
        cin >>x>>y;
        while(x--) {
            int tmp;
            cin >>tmp;
            Add(tmp,i+f,1,0);
            Add(i+f,tmp,0,0);
        }
        while(y--) {
            int tmp;
            cin >>tmp;
            Add(i+f+n,tmp+f+2*n,1,0);
            Add(tmp+f+2*n,i+f+n,0,0);
        }
    }
    cout <<ISAP(s,t,f+2*n+d+2);//传入所有节点个数
    return 0;
}

POJ3436

题目大意：略

思路：题目讲述的不是很清楚，这里有个条件，就是机器之间是流水线关系，也就是一个机器的零件输出可以作为另一个机器的零件输入，机器间可以连接且存在约束，所以题目才能转换成图上的问题来解决。多重约束求最值问题，可以使用网络流模型，可以看到，一个机器有两个属性，一个是输入，一个是输出，那么需要将属性分开，采用拆点，点直接的边权表示产能，点分为入点和出点

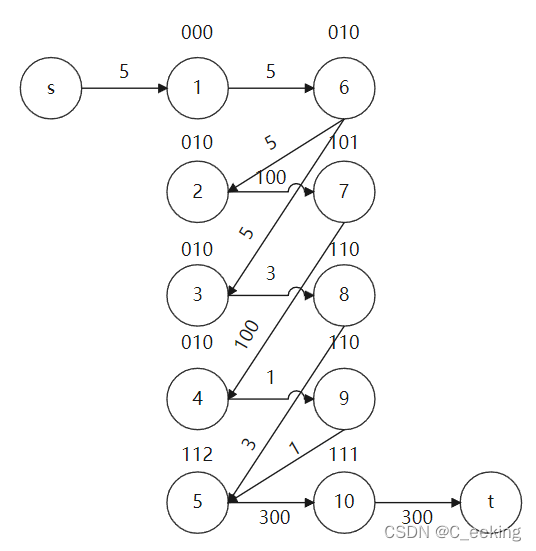
和拓扑排序类似，源点与输入不为1的节点连接，输出全为1的点与汇点连接，接下来需要确定机器间入点与出点关系，由题设，出点与入点如果需求完全匹配，显然是可以连接的，那么对 $i$ 的输出检查是否存在 $j$ 的输入，两者对应位置相等或者 $j$ 输入为2，如果存在，将 $i$ 对应出点与 $j$ 入点连接，边权为 $i$ 的产能，建好图后跑最大流即可，下图为样例2的连接图

需要注意一点的是，所求解的边不包括与源点连接和与汇点连接，标记时不能多标了路径
在这里插入图片描述

代码

#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=1e3+10;
int pre[maxn],h[maxn],g[maxn],head[maxn],p,n,cnt;
int in[121][11],out[121][11],q[121],s,t;
bool vis[121][121];
struct node {
    int cap,flow,next,to;
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt++;
}
void BFS(int t,int n) {//标初始高度
    queue<int>q;
    memset(h,-1,sizeof(h));//初始化高度
    memset(g,0,sizeof(g));//初始化计数
    h[t]=0;//汇点高度默认为0
    q.push(t);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        g[h[u]]++;//统计高度为h[u]的节点数
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(h[v]==-1) {
                h[v]=h[u]+1;
                q.push(v);
            }
        }
    }
}
int ISAP(int s,int t,int n) {//源点，汇点，点数(包括源点汇点，传入值应该为题设节点数+2)
    BFS(t,n);
    int res=0,u=s,d=inf;
    while(h[s]<n) { //整个图变成一条链，包括源点汇点
        int i=head[u];
        if(u==s)d=inf;//特判源点
        for(; ~i; i=e[i].next) { //BFS
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&h[u]==h[v]+1) {
                u=v;//更换当前点
                pre[v]=i;//记录前一条边便于增流
                d=min(d,e[i].cap-e[i].flow);//获得最小可增量
                if(u==t) {
                    while(u!=s) {
                        int j=pre[u];
                        e[j].flow+=d;
                        e[j^1].flow-=d;//增流
                        u=e[j^1].to;//回溯
                    }
                    res+=d;//累和最大流
                    d=inf;//初始化
                }
                break;
            }
        }
        if(i==-1) {//无法前进
            if(--g[h[u]]==0)break;//优化
            int hmin=n-1;//初始化
            for(int i=head[u]; ~i; i=e[i].next)//BFS
                if(e[i].cap>e[i].flow)//可行邻接点
                    hmin=min(hmin,h[e[i].to]);
            h[u]=hmin+1;
            g[h[u]]++;//对应高度计数+1
            if(u!=s)u=e[pre[u]^1].to;//继续回溯
        }
    }
    return res;
}
int main() {
    while(~scanf("%d%d",&p,&n)) {
        memset(head,-1,sizeof(head));
        memset(vis,0,sizeof(vis));
        cnt=0;
        s=0,t=2*n+1;
        for(int i=1; i<=n; i++) {
            bool flag=1;
            scanf("%d",q+i);
            Add(i,i+n,q[i],0);
            Add(i+n,i,0,0);
            for(int j=1; j<=p; j++) {
                scanf("%d",&in[i][j]);
                if(in[i][j]==1)flag=0;
            }
            if(flag) {
                Add(0,i,q[i],0);
                Add(i,0,0,0);
            }
            flag=1;
            for(int j=1; j<=p; j++) {
                scanf("%d",&out[i][j]);
                if(out[i][j]!=1)flag=0;
            }
            if(flag) {
                Add(i+n,t,q[i],0);
                Add(t,i+n,0,0);
            }
        }
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                if(i!=j) {
                    bool flag=1;
                    for(int k=1; k<=p; k++) {
                        if(out[i][k]==in[j][k]||in[j][k]==2)//判断是否连通
                            continue;
                        flag=0;
                        break;
                    }
                    if(flag) {
                        Add(i+n,j,q[i],0);
                        Add(j,i+n,0,0);
                        vis[i+n][j]=1;//该边存在
                    }
                }
        printf("%d",ISAP(s,t,t+1));
        cnt=0;//计数器，统计使用的边
        for(int i=1; i<=n; i++)
            for(int j=head[i+n]; ~j; j=e[j].next)
                if(vis[i+n][e[j].to]&&e[j].flow>0)cnt++;//如果边存在且有流量
        printf(" %d\n",cnt);
        for(int i=1; i<=n; i++)
            for(int j=head[i+n]; ~j; j=e[j].next)
                if(vis[i+n][e[j].to]&&e[j].flow>0)printf("%d %d %d\n",i,e[j].to,e[j].flow);
    }
    return 0;
}

POJ1459

题目大意：略

思路：据给出的条件建立对应的边，输电线直接建边，消费用户与汇点连接，发电厂与源点连接，最后跑最大流即可

代码

#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=3e4;
int head[maxn],g[maxn],cnt,h[maxn],pre[maxn];
int n,np,nc,m;
struct node {
    int next,to,cap,flow;//链式前向星，容量和流
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].next=head[from];
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    head[from]=cnt++;//注意是从0开始存的
}
void BFS(int t,int n) {//标初始高度
    queue<int>q;
    memset(h,-1,sizeof(h));//初始化高度
    memset(g,0,sizeof(g));//初始化计数
    h[t]=0;//汇点高度默认为0
    q.push(t);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        g[h[u]]++;//统计高度为h[u]的节点数
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(h[v]==-1) {
                h[v]=h[u]+1;
                q.push(v);
            }
        }
    }
}
int ISAP(int s,int t,int n) {//源点，汇点，点数
    BFS(t,n);
    int res=0,u=s,d=inf;
    while(h[s]<n) { //整个图变成一条链
        int i=head[u];
        if(u==s)d=inf;//特判源点
        for(; ~i; i=e[i].next) { //BFS
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&h[u]==h[v]+1) {
                u=v;//更换当前点
                pre[v]=i;//记录前一条边便于增流
                d=min(d,e[i].cap-e[i].flow);//获得最小可增量
                if(u==t) {
                    while(u!=s) {
                        int j=pre[u];
                        e[j].flow+=d;
                        e[j^1].flow-=d;//增流
                        u=e[j^1].to;//回溯
                    }
                    res+=d;//累和最大流
                    d=inf;//初始化
                }
                break;
            }
        }
        if(i==-1) {//无法前进
            if(--g[h[u]]==0)break;//优化
            int hmin=n-1;//初始化
            for(int i=head[u]; ~i; i=e[i].next)//BFS
                if(e[i].cap>e[i].flow)//可行邻接点
                    hmin=min(hmin,h[e[i].to]);
            h[u]=hmin+1;
            g[h[u]]++;//对应高度计数+1
            if(u!=s)u=e[pre[u]^1].to;//继续回溯
        }
    }
    return res;
}
int main() {
    while(cin >>n>>np>>nc>>m) {
        memset(head,-1,sizeof(head));
        //memset(pre,-1,sizeof(pre));
        cnt=0;
        char ch;
        int u,v,z;
        while(m--) {
            cin >>ch>>u>>ch>>v>>ch>>z ;
            Add(u,v,z,0);
            Add(v,u,0,0);
        }
        while(np--) {
            cin >>ch>>u>>ch>>z;
            Add(n+1,u,z,0);
            Add(u,n+1,0,0);
        }
        while(nc--) {
            cin >>ch>>u>>ch>>z;
            Add(u,n+2,z,0);
            Add(n+2,u,0,0);
        }
        cout <<ISAP(n+1,n+2,n+2)<<endl;
    }
    return 0;
}

LuoguP2763

题目大意：略

思路：依然是多约束问题，本题的最值最大只有m，因此需要判断求出的最大流值是否为m，如果不为m，代表没有合法方案

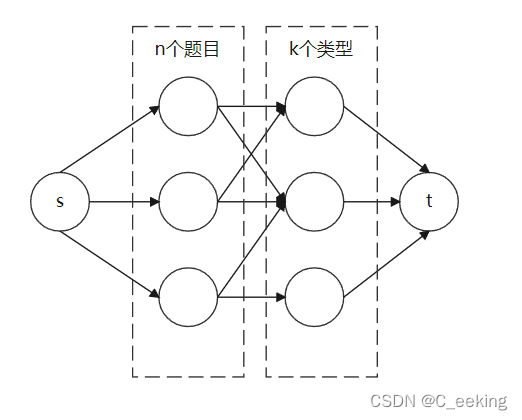
建图如下，将题目与类型之间的约束按照题设相互连接，设置源点和汇点，由于图较简单，只有四层，所以可以在回溯增流的时候记录下类型与题目的对应关系

在这里插入图片描述

代码

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=4e4+10;
int k,n,s,t,cnt,m,head[maxn/10],h[maxn/10],g[maxn/10],pre[maxn/10];
vector<int>solve[maxn/10];
struct node {
    int cap,flow,next,to;
} e[maxn];
void Add(int from,int to,int cap,int flow) {
    e[cnt].cap=cap;
    e[cnt].flow=flow;
    e[cnt].to=to;
    e[cnt].next=head[from];
    head[from]=cnt++;
}
void BFS(int t,int n) {//标初始高度
    queue<int>q;
    memset(h,-1,sizeof(h));//初始化高度
    memset(g,0,sizeof(g));//初始化计数
    h[t]=0;//汇点高度默认为0
    q.push(t);
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        g[h[u]]++;//统计高度为h[u]的节点数
        for(int i=head[u]; ~i; i=e[i].next) {
            int v=e[i].to;
            if(h[v]==-1) {
                h[v]=h[u]+1;
                q.push(v);
            }
        }
    }
}
int ISAP(int s,int t,int n) {//源点，汇点，点数(包括源点汇点，传入值应该为题设节点数+2)
    BFS(t,n);
    int res=0,u=s,d=inf;
    while(h[s]<n) { //整个图变成一条链，包括源点汇点
        int i=head[u];
        if(u==s)d=inf;//特判源点
        for(; ~i; i=e[i].next) { //BFS
            int v=e[i].to;
            if(e[i].cap>e[i].flow&&h[u]==h[v]+1) {
                u=v;//更换当前点
                pre[v]=i;//记录前一条边便于增流
                d=min(d,e[i].cap-e[i].flow);//获得最小可增量
                if(u==t) {
                    int ans=0;
                    while(u!=s) {
                        int j=pre[u];
                        e[j].flow+=d;
                        e[j^1].flow-=d;//增流
                        if(ans==1)
                            solve[u].push_back(e[j^1].to);
                        u=e[j^1].to;//回溯
                        ans++;
                    }
                    res+=d;//累和最大流
                    d=inf;//初始化
                }
                break;
            }
        }
        if(i==-1) {//无法前进
            if(--g[h[u]]==0)break;//优化
            int hmin=n-1;//初始化
            for(int i=head[u]; ~i; i=e[i].next)//BFS
                if(e[i].cap>e[i].flow)//可行邻接点
                    hmin=min(hmin,h[e[i].to]);
            h[u]=hmin+1;
            g[h[u]]++;//对应高度计数+1
            if(u!=s)u=e[pre[u]^1].to;//继续回溯
        }
    }
    return res;
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin >>k>>n;
    memset(head,-1,sizeof(head));
    s=0,t=n+k+1;
    for(int i=1; i<=n; i++) {
        Add(0,i,1,0);
        Add(i,0,0,0);
    }
    for(int i=1; i<=k; i++) {
        int x;
        cin >>x;
        m+=x;
        Add(n+i,t,x,0);
        Add(t,n+i,0,0);
    }
    for(int i=1; i<=n; i++) {
        int p;
        cin >>p;
        while(p--) {
            int x;
            cin >>x;
            Add(i,n+x,1,0);
            Add(n+x,i,0,0);
        }
    }
    if((ISAP(s,t,n+2)^m))cout <<"No Solution!";
    else
        for(int i=n+1; i<=n+k; i++) {
            int len=solve[i].size();
            sort(solve[i].begin(),solve[i].end());
            cout <<i-n<<":";
            for(int j=0; j<len; j++)
                cout <<" "<<solve[i][j];
            cout <<endl;
        }
    return 0;
}
/*
2 2
1 1
1 1
1 2
*/

总结

ISAP算法属于求解最大流的一种方法，对于稠密图来说效果较好，其复杂度主要与点的个数有关，一般来说，多约束求最值问题都可以以网络流的思路去考虑，并且，对于题目中所给对象若有两个属性，要善于将属性拆分，构造连接，从而便于建图求解网络流，从练习题来看，ISAP代码量较大，但是对输出最大流方案的题目实现输出较为简单