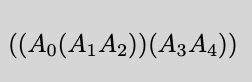dynamic programming

矩阵链式乘法

确定结合律使用顺序以达到最小乘法次数

错误使用递归实现动态规划的例子

复杂度 $O(2^n)$ ，由递推方程通过数学归纳法可证

#include <vector>
#include <iostream>
using namespace std;

typedef vector<vector<int>> Matrix;
class Solution{
public:
    int recurMatrixChain(vector<int> &P, int lo, int hi){
        if (lo >= hi-1) return 0;
        int res = INT_MAX;
        for(int mid = lo+1; mid < hi; mid++){
            int tmp = recurMatrixChain(P, lo, mid)+recurMatrixChain(P, mid, hi)+P[lo]*P[mid]*P[hi];
            res = tmp < res ? tmp : res;
        }
        return res;
    }
};

int main(int argc, const char * argv[]) {
    unsigned seed = time(0);
    srand(seed);
    vector<int> p;
    int n = 4;
    for (int i = 0; i < n; i++){
        p.push_back((rand()%100)+1);
    }
    for (int i : p){
        cout << i << ',';
    }
    cout << endl;
    Solution s;
    cout << s.recurMatrixChain(p, 0, n-1) << endl;
    return 0;
}

使用迭代实现动态规划

建立备忘录 $O(n^3)$ ，通过标记函数获得最终括弧添加位置 $O (n)$

#include <vector>
#include <stack>
#include <iostream>
#include <fstream>
#include <list>
#include <sys/stat.h>

using namespace std;
typedef vector<vector<int>> Matrix;

class Solution{
private:
    struct TreeNode{
        string val;
        TreeNode *lc, *rc;
    };
    vector<vector<int>> memo, mark; //备忘录与标记函数，标记函数在某些dp问题中不必需
    TreeNode* root;
public:
	//主算法
    int iterateMatrixChain(vector<int> &p){
        int n = p.size();
        memo = vector<vector<int>> (n-1, *new vector<int>(n-1, 0));
        mark = vector<vector<int>> (n-1, *new vector<int>(n-1, 0));
        for (int numberOfMatrices = 2; numberOfMatrices < n; numberOfMatrices++){
            for (int lo = 0; lo < n-numberOfMatrices; lo++){
                int hi = lo+numberOfMatrices-1;
                int least = INT_MAX;
                for (int endOfFirst = lo; endOfFirst < hi; endOfFirst++){
                    int startOfSecond = endOfFirst+1;
                    int tmp = memo[lo][endOfFirst] + memo[startOfSecond][hi] + p[lo]*p[startOfSecond]*p[hi+1];
                    if (tmp < least){
                        least = tmp;
                        memo[lo][hi] = tmp;
                        mark[lo][hi] = endOfFirst;
                    }
                }
            }
        }
        root = establish(mark, 0, n-2);
        return memo[0][n-2];
    }
    //建立表达式树
    TreeNode* establish(vector<vector<int>> &mark, int lo, int hi){
        TreeNode* cur = new TreeNode();
        if (lo == hi){
            cur->val = to_string(lo);
        }else{
            cur->val = ".";
            int mid = mark[lo][hi];
            cur->lc = establish(mark, lo, mid);
            cur->rc = establish(mark, mid+1, hi);
        }
        return cur;
    }
    //扁平化，以将括弧插入字符串
    list<string> inorder(TreeNode* cur){
        list<string> l;
        if (cur->val.compare(".") != 0){
            l.push_back("A_{");
            l.push_back(cur->val);
            l.push_back("}");
        }else{
            l.push_back("(");
            l.splice(l.end(), inorder(cur->lc));
            l.splice(l.end(), inorder(cur->rc));
            l.push_back(")");
        }
        return l;
    }
    //对外提供调用接口
    list<string> getSequence(){
        return inorder(root);
    }
};

//main(int argc, const char * argv[])测试程序中涉及文件io
int main(int argc, const char * argv[]) {
    vector<int> p = {30,35,15,5,10,20};
    Solution s;
    s.iterateMatrixChain(p);
    list<string> l = s.getSequence();
    string format1 = R"(\documentclass[10pt]{article}
\usepackage[usenames]{color} %used for font color
\usepackage{amssymb} %maths
\usepackage{amsmath} %maths
\usepackage[utf8]{inputenc} %useful to type directly diacritic characters
\begin{document}
\begin{align*})";
    string format2 = R"(\end{align*}
\end{document})";
    ofstream fs;
    fs.open("yourOwnWorkspace/matrix.tex", ios::out);
    fs << format1;
    for (auto i : l){
        fs << i;
    }
    fs << format2;
    fs.close();
    fs.open("yourOwnWorkspace/openlatex.sh", ios::out);
    fs << R"(cd yourOwnWorkspace)" << endl;
    fs << R"(latex ./matrix.tex)" << endl;
    fs << R"(dvipdf ./matrix.dvi)" << endl;
    fs.close();
    chmod("yourOwnWorkspace/openlatex.sh", S_IEXEC);
    system("yourOwnWorkspace/openlatex.sh");
    return 0;
}