环形链表
Notes:
①使用方法一,哈希表,可以很便捷的就判断链表是否闭环,并且拿到闭环的头节点。缺点是效率不高,我提交代码时运行了3ms,时间复杂度和空间复杂度都不占优。(方法一在下面。)
②使用方法二,快慢指针,是利用快指针追赶慢指针的原理,慢指针每走一步,快指针就走两步,这样快指针迟早会追上慢指针。且快指针始终走慢指针的两倍路程。
// Definition for singly-linked list.
// class ListNode {
// int val;
// ListNode next;
// ListNode(int x) {
// val = x;
// next = null;
// }
// }
public class Solution {
public boolean hasCycle(ListNode head) {
// 方法二:利用快慢指针。效率更高。
if (head == null || head.next == null)
return false;
// 这一句过后,至少有两个节点。
ListNode i = head, j = head;
while (j != null) {
// j若是为null,则肯定不是闭环。
i = i.next;
if (j.next == null)
break;
j = j.next.next;
if (i == j)
return true;
}
return false;
// 21/21 cases passed (0 ms)
// Your runtime beats 100 % of java submissions
// Your memory usage beats 5.31 % of java submissions (42.5 MB)
}
}
// @lc code=end
// 方法一:利用哈希表存放的元素不能重复,遍历链表放入哈希表中,判断有没有闭环。
Set<ListNode> set = new HashSet<>();
while (head != null) {
if (!set.add(head)) {
return true;
}
head = head.next;
}
return false;
环形链表 II

Notes:
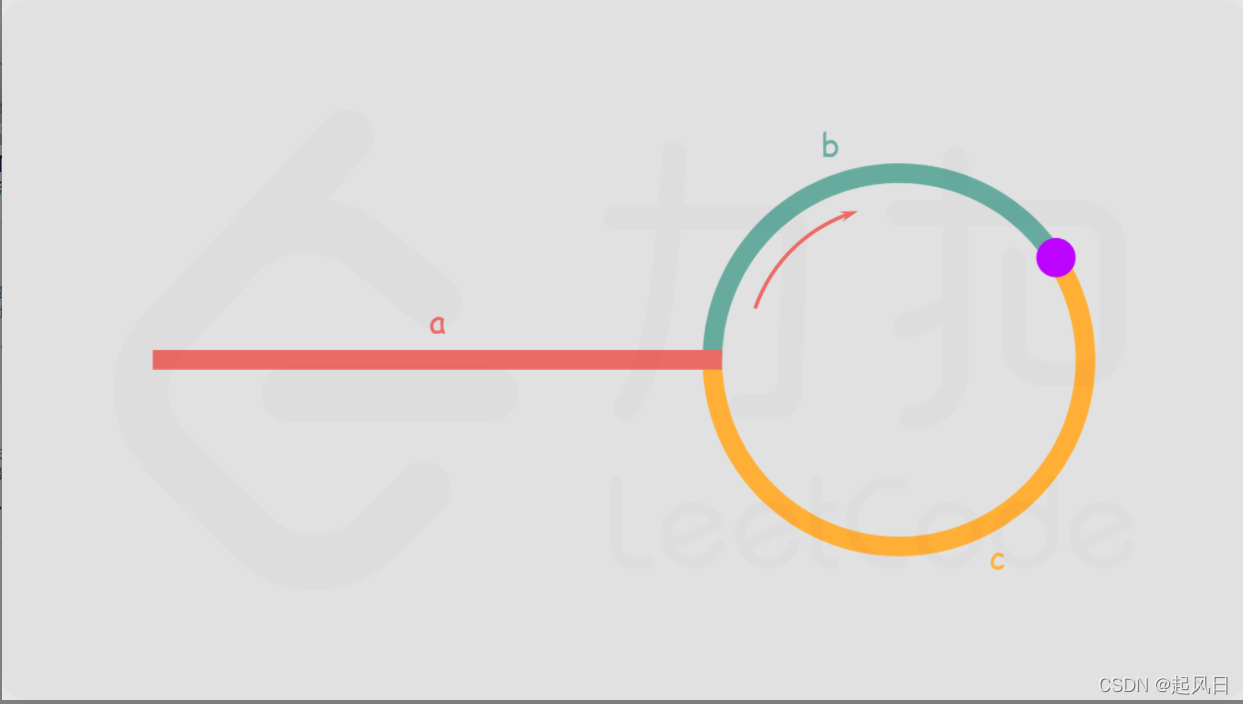
这道题是上一道题的进阶,需要找到闭环的头。如果给的链表头尾相连,那么相遇点就是头节点,那上一题的代码几乎不用改动,返回相遇节点就可以了。但是题目给的链表不是首尾相连,相遇点可能不是闭环头,情况如图所示。
那么问题来了,找到相遇点了,但是头节点怎么找。我在这里卡住了。
于是我就去看了官方答案。发现如果不使用哈希表而是快慢指针的话,这道题需要列表达式理解。
上图显示:a表示起点到闭环头的距离。b表示闭环头到相遇点的距离。c表示闭环长-b。
由于快指针始终是慢指针的两倍。
相遇时,
慢针走a+b,
快针走a + n(b+c) + b
n表示快针在慢针走到相遇点之前走了多少圈。
有 a + n(b + c) + b = 2(a + b)
简化后 a = c + (n-1)(c+b)
a这段距离等于c + n-1圈闭环长。
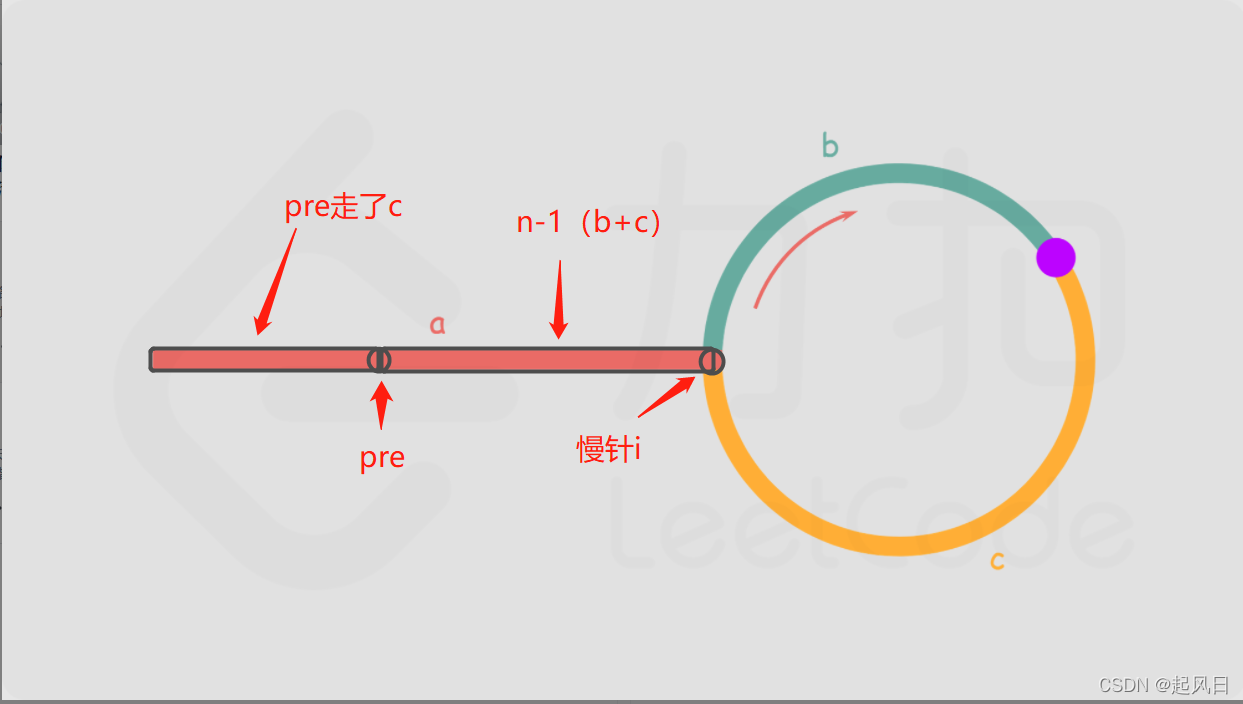
当快慢针相遇时,表示该链表一定是闭环,这时候在放一个指针pre从头开始跑,慢指针也开始跑。pre跑c的距离,慢指针刚刚好在闭环头上。
pre跑a的距离,慢指针再跑n-1圈,会相遇再闭环头,返回这个pre即可。
// @lc code=start
/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
// 方法二:利用快慢指针。效率更高。i是慢指针,j是快指针。
if (head == null || head.next == null)
return null;
// 这一句过后,至少有两个节点。
ListNode i = head, j = head;
while (j != null) {
// j若是为null,则肯定不是闭环。
i = i.next;
if (j.next == null)
break;
j = j.next.next;
if (i == j) {
ListNode pre = head;
while (pre != i) {
pre = pre.next;
i = i.next;
}
return pre;
}
}
return null;
}
}
// @lc code=end
// 方法一:哈希表。
Set<ListNode> set = new HashSet<>();
while(head!=null){
if (!set.add(head)) {
return head;
}
head = head.next;
}
return null;