求组合数

1.递推法
【题目链接】AcWing 885. 求组合数 I - AcWing

递推公式:

解释:从a个苹果中取出b个苹果的方案数:从a个苹果中先挑出1个红苹果,因此还剩下a-1个苹果,总选取方案数将从这a-1个苹果中产生,分为包含与不包含这个红色的苹果:
-
包含:从
a - 1个苹果中再选取b-1个(已经有一个红色苹果了) -
不包含:从
a - 1个苹果中再选取b个
由分类加法原则:总方案数 = 上述两个方案数之和
【核心代码】
时间复杂度:O(N * N)
const int N = 2010;
void init()
{
for(int i = 0; i < N; i ++)
for(int j = 0; j <= i; j ++)
if(!j) c[i][j] = 1;// 从i个苹果中选取0个——只有一种方案那就是不选
else
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;// 递推公式
}
2.定义法
【题目链接】886. 求组合数 II - AcWing题库
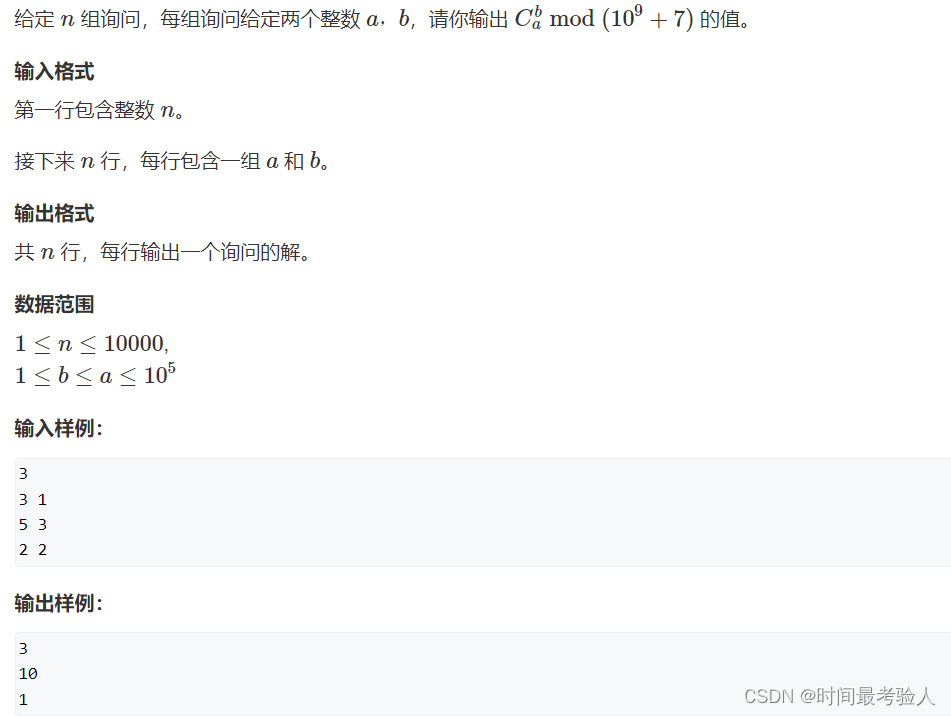
如果我们还用求组合数1的递推式来解决本题,时间复杂度为O(N*N),那就会超时了,因此我们先要对数据进行预处理,优化时间复杂度
思路:
除相当于乘于它的逆元!因此,我们要预处理出来阶乘

**求逆元:**快速幂 + 费马小定理
∵mod=1e9+7是质数,所以2~1e9+6与1e9+7互质,所以可以使用费马小定理来求解逆元,逆元通过快速幂求解。
【代码实现】
时间复杂度:O(N?log(N))
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p) // 求a^k mod p
{
int res = 1;
while(k)
{
if(k & 1) res = (LL)res * a % p;
a = (LL) a * a % p;
k >>= 1;
}
return res;
}
int main()
{
int n;
cin >> n;
//先预处理出来阶乘(阶乘和逆元阶乘)
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i ++)
{
fact[i] = (LL)fact[i - 1] * i % mod;// 防止溢出转为long long
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
while (n -- )
{
int a, b;
cin >> a >> b;
//mod两次是为了防止结果过大,导致溢出
cout << (LL)fact[a] * infact[b] % mod * infact[a - b] % mod << endl;
}
return 0;
}
3.定义 + Lucas定理
【题目链接】887. 求组合数 III - AcWing题库

每组询问的数据的范围爆大!1~10^18,用求组合数2肯定会超时!但p:1~10^5
思路:定义组合数 + 卢卡斯定理
组合数定义:

卢卡斯定理:
卢卡斯定理是一个与组合数有关的数论定理,在算法竞赛中用于求组合数对某质数的模。

【代码实现】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
//快速幂
LL qmi(LL a, LL k, int p)
{
LL res = 1;
while(k)
{
if(k & 1) res = res * a % p;
a = a * a % p;
k >>= 1;
}
return res;
}
//定义求组合数
LL C(LL a, LL b, int p)
{
if(b > a) return 0;
LL res = 1;
for(int i = 1, j = a; i <= b; i ++, j --)
{
res = res * j % p;
res = res * qmi(i, p - 2, p) % p;
}
return res;
}
// 卢卡斯定理
LL lucas(LL a, LL b, int p)
{
if(a < p && b < p) return C(a, b, p);
return C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;//保证a和b足够小,所以要一直递归。
}
int main()
{
int n;
cin >> n;
while (n -- )
{
LL a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
4.定义 + 高精度
【题目链接】888. 求组合数 IV - AcWing题库
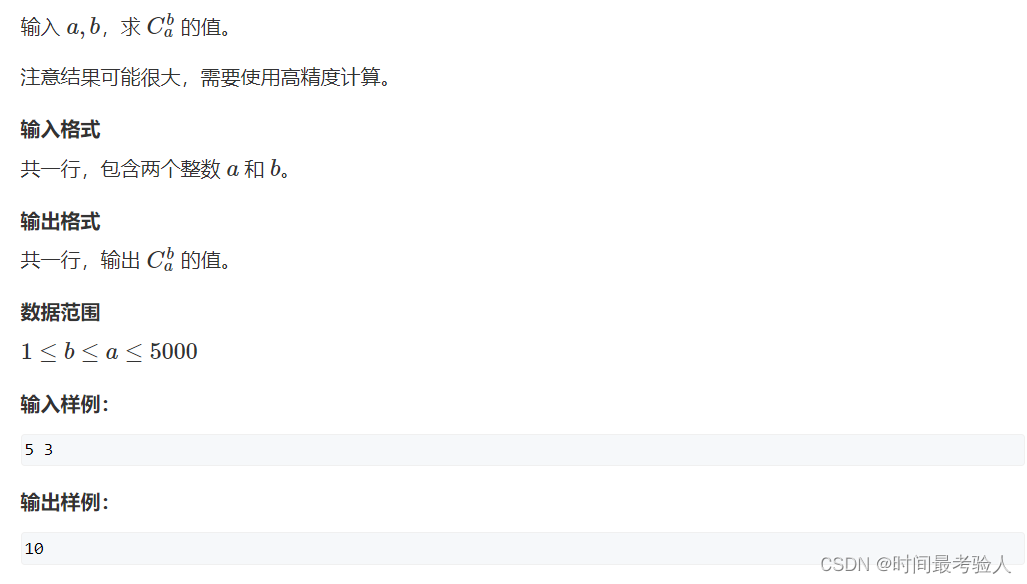
上述三种求组合数都是取模操作,我们就需要进行高精度计算,我们当然可以直接使用高精度乘法和除法,但代码量会有点大。
思路:
我们对组合数进行分解质因数,如下图,且仅需用高精度乘法即可实现!
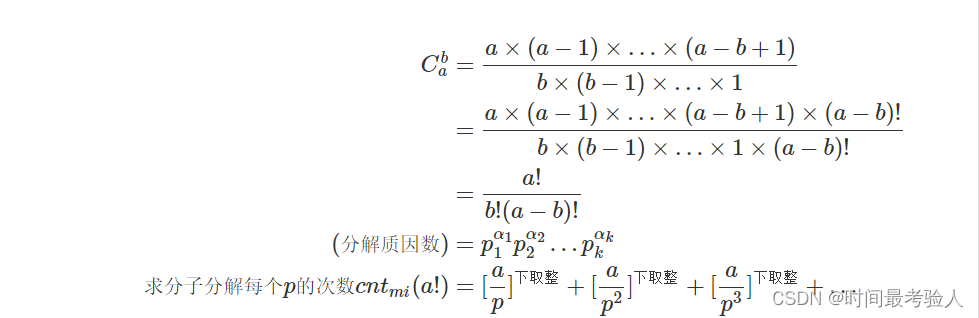
则组合数的质因数的幂为分子的质因数的幂减去分母的对应的质因数的幂。

【代码实现】
时间复杂度:O(N)
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 5010;
int primes[N];
int sum[N];
bool st[N];
int cnt;
void get_primes(int n)
{
for(int i = 2; i <= n; i ++)
{
if(!st[i]) primes[cnt ++] = i;
for(int j = 0; i * primes[j] <= n; j ++)
{
st[primes[j] * i] = true;
if(i % primes[j] == 0) break;
}
}
}
int get(int n, int p)//求n的阶乘里包含的p的个数
{
int res = 0;
while (n)
{
res += n/p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b)
{
vector<int> c;
int t = 0;
for(int i = 0; i < a.size(); i ++)
{
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while(t)
{
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main()
{
int a, b;
cin >> a >> b;
//1.筛质数
get_primes(a);
//2. 求质数出现的个数
for(int i = 0; i < cnt; i ++)
{
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
//3. 高精度乘法
vector<int> res;
res.push_back(1);
for(int i = 0; i < cnt; i ++)
for(int j = 0; j < sum[i]; j ++)
res = mul(res, primes[i]);
for(int i = res.size() - 1; i >= 0; i --) cout << res[i];
return 0;
}
总结
上述是对算法竞赛中求组合数的几种常用方法,在理解原理的基础上,熟记并能快速打出核心代码!
部分内容参考学习:
1.acwing算法基础课
注:如果文章有任何错误或不足,请各位大佬尽情指出,评论留言留下您宝贵的建议!如果这篇文章对你有些许帮助,希望可爱亲切的您点个赞推荐一手,非常感谢啦

欢迎访问:本人博客园地址