2045. 到达目的地的第二短时间
2022.1.24 每日一题
题目描述
城市用一个 双向连通 图表示,图中有 n 个节点,从 1 到 n 编号(包含 1 和 n)。图中的边用一个二维整数数组 edges 表示,其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通,顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。
每个节点都有一个交通信号灯,每 change 分钟改变一次,从绿色变成红色,再由红色变成绿色,循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点,但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ,你 不能 在节点等待,必须离开。
第二小的值 是 严格大于 最小值的所有值中最小的值。
例如,[2, 3, 4] 中第二小的值是 3 ,而 [2, 2, 4] 中第二小的值是 4 。
给你 n、edges、time 和 change ,返回从节点 1 到节点 n 需要的 第二短时间 。
注意:
你可以 任意次 穿过任意顶点,包括 1 和 n 。
你可以假设在 启程时 ,所有信号灯刚刚变成 绿色 。
示例 1:
输入:n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出:13
解释:
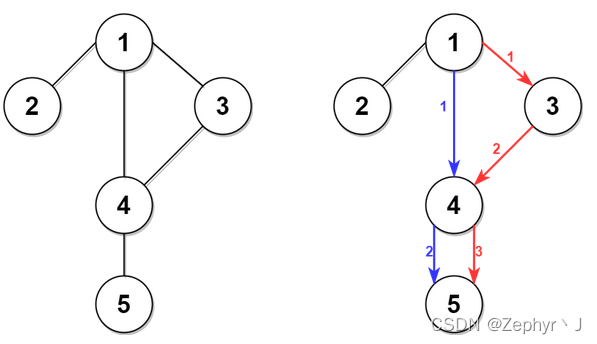
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是:
-从节点 1 开始,总花费时间=0
-1 -> 4:3 分钟,总花费时间=3
-4 -> 5:3 分钟,总花费时间=6
因此需要的最小时间是 6 分钟。
?
右图中的红色路径是第二短时间路径。
-从节点 1 开始,总花费时间=0
-1 -> 3:3 分钟,总花费时间=3
-3 -> 4:3 分钟,总花费时间=6
-在节点 4 等待 4 分钟,总花费时间=10
-4 -> 5:3 分钟,总花费时间=13
因此第二短时间是 13 分钟。
示例 2:
输入:n = 2, edges = [[1,2]], time = 3, change = 2
输出:11
解释:
最短时间路径是 1 -> 2 ,总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ,总花费时间 = 11 分钟
提示:
2 <= n <= 10^4
n - 1 <= edges.length <= min(2 * 10^4, n * (n - 1) / 2)
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 10^3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
我想的办法纯粹是基于最短路的想法走的,也就是bfs过程中,点不会重复到达,所以一直不知道怎么计算出第二段的路径
然后看了答案,从这个想法中跳出来,当每个点可以多次到达的情况下,就可以实现第二短路径的求解
但是在这个过程中,还需要注意的就是如果无限次的移动,那么可能时间很长,所以,每个点只记录第一次和第二次到达的时间,而不去管再长的时间,因为第三次到达任意点的时间不可能是结果路径中的,这个比较关键
最后就是知道走几步以后加上红绿灯的时间计算,这个相对简单,就是简单的数学计算
class Solution {
public int secondMinimum(int n, int[][] edges, int time, int change) {
//这个题看上去就有点难,一般都是找最短时间,这个是第二短,还有红绿灯...
//最短,仔细想了一下,两种可能,第一种可能就是和示例1一样,就是第二短的时间
//还有一种可能就是到了终点再返回上一个点,然后再到终点
//所以还是用bfs进行扩散,因为每两个点之间的时间都是固定的,所以应该可以写
//关键问题是怎么找第二短的路径
//其实可以想到一个方法,就是先找最短的路径,然后将最短路径在所有路径中删除
//然后找到的就是第二短的路径,但是这个删除操作确实不知道怎么做
//然后又想到一个方法,刚刚说到第二短就是两种时间的比较,而要比达到终点打个来回时间还短的话(这样是多走了两个点)
//那必须是多走一个点,也就是示例1的情况
//这就提醒我们可以检查是否多走一个点也可以到达终点,如果可以,返回这个时间;不可以,直接返回另一种情况的时间
//那么怎么检查是否可以多走一个点呢
//想了半天,不知道怎么走,想到的办法就是记录每个点到达终点的最小步数,用dfs来实现
//要用bfs就不能把走过的点丢弃
//先用map存储路径,存储每个点能到达的其他所有点
Map<Integer, List<Integer>> map = new HashMap<>();
for(int[] edge : edges){
int pos1 = edge[0];
int pos2 = edge[1];
List<Integer> list1 = map.getOrDefault(pos1, new ArrayList<>());
List<Integer> list2 = map.getOrDefault(pos2, new ArrayList<>());
list1.add(pos2);
list2.add(pos1);
map.put(pos1, list1);
map.put(pos2, list2);
}
Queue<Integer> queue = new LinkedList<>();
queue.offer(1);
//到达当前点的最短时间和第二短时间
int[][] len = new int[n + 1][2];
for(int i = 1; i <= n; i++){
len[i][0] = Integer.MAX_VALUE;
len[i][1] = Integer.MAX_VALUE;
}
len[1][0] = 0;
int idx = 0; //第几次扩散
//如果最终结果没有被更新,则一直循环
while(len[n][1] == Integer.MAX_VALUE){
idx++;
int size = queue.size();
while(size-- > 0){
int top = queue.poll();
List<Integer> list = map.get(top);
//从top开始扩散
for(int p : list){
//如果比最小的小,那么更新,因为是bfs,所以第一次遍历到的肯定是最小的
if(len[p][0] > idx){
len[p][0] = idx;
queue.offer(p);
//如果比第二小的小,那么更新
}else if(len[p][0] < idx && len[p][1] > idx){
len[p][1] = idx;
queue.offer(p);
}
//如果第三次经过这个点,到达终点的时间不可能比第二次小,所以不做记录
}
}
}
//计算时间
int count = len[n][1];
int res = 0;
for(int i = 0; i < count; i++){
//第几次变色
int temp = res / change;
//如果当前次数是奇数,那么就是红灯
if(temp % 2 == 1){
//红灯需要等待的时间是(change - (res - temp * change))
res += time + (change - (res - temp * change));
}else{
res += time;
}
}
return res;
}
}
1688. 比赛中的配对次数
2022.1.25 每日一题
题目描述
给你一个整数 n ,表示比赛中的队伍数。比赛遵循一种独特的赛制:
如果当前队伍数是 偶数 ,那么每支队伍都会与另一支队伍配对。总共进行 n / 2 场比赛,且产生 n / 2 支队伍进入下一轮。
如果当前队伍数为 奇数 ,那么将会随机轮空并晋级一支队伍,其余的队伍配对。总共进行 (n - 1) / 2 场比赛,且产生 (n - 1) / 2 + 1 支队伍进入下一轮。
返回在比赛中进行的配对次数,直到决出获胜队伍为止。
示例 1:
输入:n = 7
输出:6
解释:比赛详情:
-第 1 轮:队伍数 = 7 ,配对次数 = 3 ,4 支队伍晋级。
-第 2 轮:队伍数 = 4 ,配对次数 = 2 ,2 支队伍晋级。
-第 3 轮:队伍数 = 2 ,配对次数 = 1 ,决出 1 支获胜队伍。
总配对次数 = 3 + 2 + 1 = 6
示例 2:
输入:n = 14
输出:13
解释:比赛详情:
-第 1 轮:队伍数 = 14 ,配对次数 = 7 ,7 支队伍晋级。
-第 2 轮:队伍数 = 7 ,配对次数 = 3 ,4 支队伍晋级。
-第 3 轮:队伍数 = 4 ,配对次数 = 2 ,2 支队伍晋级。
-第 4 轮:队伍数 = 2 ,配对次数 = 1 ,决出 1 支获胜队伍。
总配对次数 = 7 + 3 + 2 + 1 = 13
提示:
1 <= n <= 200
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-of-matches-in-tournament
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
妙
class Solution {
public int numberOfMatches(int n) {
//每次比赛淘汰一个队,剩余一个队就要淘汰n-1个队,比赛就要进行n - 1次
return n - 1;
}
}
2013. 检测正方形
2022.1.26 每日一题
题目描述
给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法:
添加 一个在数据流中的新点到某个数据结构中。可以添加 重复 的点,并会视作不同的点进行处理。
给你一个查询点,请你从数据结构中选出三个点,使这三个点和查询点一同构成一个 面积为正 的 轴对齐正方形 ,统计 满足该要求的方案数目。
轴对齐正方形 是一个正方形,除四条边长度相同外,还满足每条边都与 x-轴 或 y-轴 平行或垂直。
实现 DetectSquares 类:
DetectSquares() 使用空数据结构初始化对象
void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造 轴对齐正方形 的方案数。
示例:
输入:
[“DetectSquares”, “add”, “add”, “add”, “count”, “count”, “add”, “count”]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
输出:
[null, null, null, null, 1, 0, null, 2]
解释:
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择:
// - 第一个,第二个,和第三个点
detectSquares.count([14, 8]); // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]); // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择:
// - 第一个,第二个,和第三个点
// - 第一个,第三个,和第四个点
提示:
point.length == 2
0 <= x, y <= 1000
调用 add 和 count 的 总次数 最多为 5000
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/detect-squares
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
当时周赛的时候不知道咋回事,套了两层,导致超时了
今天写的时候很简单就写出来了,虽然有些地方罗嗦了点
不难,就是根据两个确定的点,确定其他两个正方形点的位置,并且看这两个位置是否存在
注意有重复的点
class DetectSquares {
//基本上是最后一次打周赛的题了,记得当时超时了
//给定一个点,找一个正方形,相当于找边,所以做法就是找一个和该点相同行或者列的点,
//然后计算边长,从而确定其他两个点的位置
//我不用看也知道当时是这样做的,然后发现过了的都是按照边长来找点,这样做的
//前提都是要将这些点放在 行 列 两个集合中
//里面的map表示点的个数
Map<Integer, Map<Integer, Integer>> row;
Map<Integer, Map<Integer, Integer>> col;
public DetectSquares() {
row = new HashMap<>();
col = new HashMap<>();
}
public void add(int[] point) {
int r = point[0];
int c = point[1];
Map<Integer, Integer> rin = row.getOrDefault(r, new HashMap<>());
Map<Integer, Integer> cin = col.getOrDefault(c, new HashMap<>());
//将数组转换成一个整数
int temp = r * 1001 + c;
rin.put(temp, rin.getOrDefault(temp, 0) + 1);
cin.put(temp, cin.getOrDefault(temp, 0) + 1);
row.put(r, rin);
col.put(c, cin);
}
public int count(int[] point) {
int r = point[0];
int c = point[1];
//遍历所有边长
//如果没有这一行的点,那么直接返回0
if(!row.containsKey(r) || !col.containsKey(c))
return 0;
//当前点,当前点的数目不用管
int temp = r * 1001 + c;
Map<Integer, Integer> rin = row.get(r);
Map<Integer, Integer> cin = col.get(c);
int res = 0;
for(int p : rin.keySet()){
//如果是重合了,跳过
if(p == temp)
continue;
//这个点的数目
int count1 = rin.get(p);
int rr = p / 1001;
int cc = p % 1001;
//边长
int len = Math.abs(cc - c);
//此时确定了一条边,还需要确定一条横边,这条横边可以在上面或者下面
int rup = rr + len;
int rdown = rr - len;
if(row.containsKey(rup)){
Map<Integer, Integer> rrup = row.get(rup);
int p2 = rup * 1001 + c;
int p3 = rup * 1001 + cc;
if(rrup.containsKey(p2) && rrup.containsKey(p3)){
res += rrup.get(p2) * rrup.get(p3) * count1;
}
}
if(row.containsKey(rdown)){
Map<Integer, Integer> rrdown = row.get(rdown);
int p2 = rdown * 1001 + c;
int p3 = rdown * 1001 + cc;
if(rrdown.containsKey(p2) && rrdown.containsKey(p3)){
res += rrdown.get(p2) * rrdown.get(p3) * count1;
}
}
}
return res;
}
}
/**
* Your DetectSquares object will be instantiated and called as such:
* DetectSquares obj = new DetectSquares();
* obj.add(point);
* int param_2 = obj.count(point);
*/