[数据结构与算法]路径规划与优化学习系列（一）---路径规划算法

路径规划与优化学习系列（一）—路径规划算法

前言

几个月来浑浑噩噩，人生这张地图实在太大了，顿时觉得人生之路障碍重重、迷茫不清，故此受人启发，一学路径规划之法，以解心头之困，以便找到寻找最优之人生路（结尾有人生之悟）

本文仅用于笔记和回顾，学习来源如下介绍

学习目标

1. 入门路径规划思想
2. 深入了解经典路径规划思想
3. 深入体会各种经典算法的适用场景
4. 深入理解经典算法的代码实现
5. 泛读论文，探索算法改进点

学习来源

1. B站（IR艾若机器人）机器人路径规划、轨迹优化系列课程_哔哩哔哩_bilibili

2. 中国知网、SCI、ieee论文库

正文

一、路径规划思想概述

? 近年来，路径规划算法高效发展，得到广泛应用。以无人机路径规划为例，主要包括

1.基于飞行区域

• PRM概率路径图法（避免碰撞）
• 分区规划+K-means+模拟退火（复杂约束下多任务多机）
• 人工势场（解决目的点无法准确到达）
• A*定长搜索（起始点确切路径）
• voronoi加权方向图+蚁群算法（高效避障）

2.基于任务时间

• 时间最优+服务结点最大化
• 通信优化框架

3.基于能耗优化

• A*+粒子群优化（路线最优、降低能耗）
• 多机联合+比特分配（满足quality并且降低能耗）

4.基于任务分配

• 动态贝叶斯网络架构（动态飞行复杂环境中的自主飞行和任务执行）
• 异构无人机与多样化任务适配（自然灾害和环境多变下的飞行）

参考：无人机路径规划算法研究_魏涛 DIO:10.27675/d.cnki.gcydx.2020.000204

二、路径规划经典算法

（一）基于搜索的路径规划

1.Dijkstra

背景及适用场景

• 从起始点到终点的最短（最优）路径问题
• 广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，最终得到一个最短路径树。该算法常用于路径搜索或者作为其他图算法的一个子模块
• 本算法也可适用于寻优问题

原理：贪心思想

从起点开始逐步扩展，每一步为一个节点找到最短路径

栅格地图

• 定义：地图划分为若干分辨率的小方格，每个小方格有不同的权值（颜色），代表不同的意义，如下：
  

• 栅格地图的优势：

  • 可以将任意形状轮廓的地图，用足够精细的栅格进行绘制

  • 每一个栅格，可以通过不同颜色表示不同含义

  • 基于栅格地图进行路径规划有横、纵、斜三个规划方向。对应室内低速机器人可以完全按照路径行走；对于中高速机器人，可以考虑将路径进行平滑处理，以适用于非完全约束系统。

• 有权图转化：

  

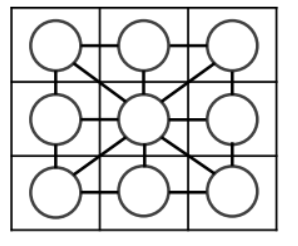
  行动方向矩阵：前两个参数代表运动方向，后一个参数代表运动代价（通常为运动距离）

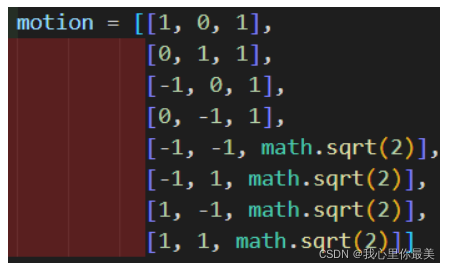
• matlab绘制栅格地图

  % MATLAB 绘制栅格地图的核心函数和思想
  % colormap：为栅格地图创建自定义颜色。如黄色栅格代表的起点，红色栅格代表的终点,黑色栅格代表的障碍物
  % sub2ind：将行列索引转为线性索引  ind2sub：将线性索引转为行列索引
  % image：利用colormap建立的颜色图，将数组信息显示为图像
  clc;
  clear;
  close all;
  cmap = [1 1 1; ...       % 1-白色-空地
      0 0 0; ...           % 2-黑色-静态障碍
      1 0 0; ...       % 3-红色-动态障碍
      1 1 0; ...           % 4-黄色-起始点
      1 0 1; ...           % 5-品红-目标点
      0 1 0; ...           % 6-绿色-到达目标点的规划路径
      0 1 1];              % 7-青色-动态规划的路径
  
  % 构建颜色map图
  colormap(cmap);    
  
  %% 构建栅格地图场景
  % 栅格地图界面大小：行数和列数
  rows = 10;
  cols = 20;
  % 定义栅格地图的全域，并初始化空白地图
  field = ones(rows,cols);
  
  % 障碍物区域
  obsRate = 0.3;
  obsNum  = floor(rows * cols * obsRate); % 取整
  obsIndex = randi([1,rows*cols],obsNum,1);
  field(obsIndex) = 2;
  
  % 起始点和目标点
  startPos = 2;
  goalPos = rows * cols - 2;
  field(startPos) = 4;
  field(goalPos) = 5;
  
  %% 画栅格图
  image(1.5,1.5,field);
  grid on;
  set(gca , 'gridline' , '-' , 'gridcolor' , 'k' , 'linewidth' , 2 , 'GridAlpha' , 0.5);
  set(gca , 'xtick' , 1 : cols + 1,'ytick',1 : rows + 1);
  axis image;
  

具体实现

取自：IR艾若机器人

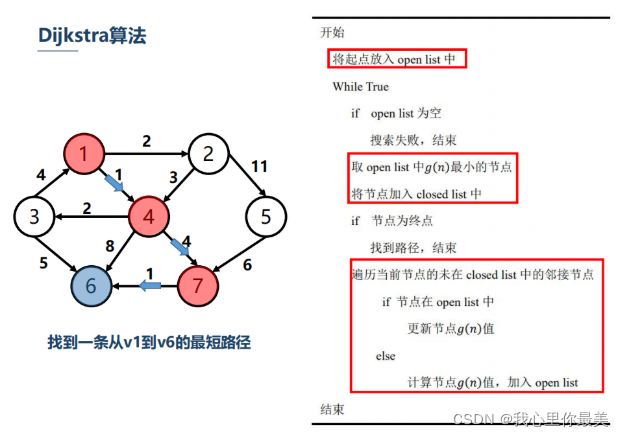
2.A*

背景及适用场景

• 从起始点到终点的最短（最优）路径问题
• 广度优先搜索:BFS以起点A为圆心，先搜索A周围的所有点，形成一个类似圆的搜索区域，再扩大搜索半径，进一步搜索其它没搜索到的区域，直到终点B进入搜索区域内被找到
• 深度优先搜索:DFS则是让搜索的区域离A尽量远，离B尽量近

原理：启发式函数

• A*算法的导出

  首先，BFS保证的是从起点到达路线上的任意点花费的代价最小（但是不考虑这个过程是否要搜索很多格子）。其次，DFS保证的是通过不断矫正行走方向和终点的方向的关系，使发现终点要搜索的格子更少（但是不考虑这个过程是否绕远）。

  因此，A*算法的设计同时融合了BFS和DFS的优势，既考虑到了从起点通过当前路线的代价（保证了不会绕路），又不断的计算当前路线方向是否更趋近终点的方向（保证了不会搜索很多图块），是一种静态路网中最有效的直接搜索算法。

• 启发式函数

设定地图为栅格地图，运动方向有八个，每个方向都有对应的代价

• F(n)为总代价函数

• g(n)为起点移动到指定结点（当前结点）的代价值

• h(n)为启发式函数，用来约束路径的走向，代表指定结点（当前结点）到终点的横向或者纵向代价值

• A*算法的优势：减少了采样栅格个数，增加了路径搜索速度，优化了路径走向

具体实现

（二）基于采样的路径规划

1.RRT

定义及适用场景

快速拓展随机树法

单源路径、避障问题

核心思想

• 主体思想

  将搜索的起点位置作为根节点，然后通过随机采样增加叶子节点的方式，生成一个随机扩展树，当随机树的叶子节点进入目标区域（故不能准确找到目标点），就得到了从起点位置到目标位置的路径

  

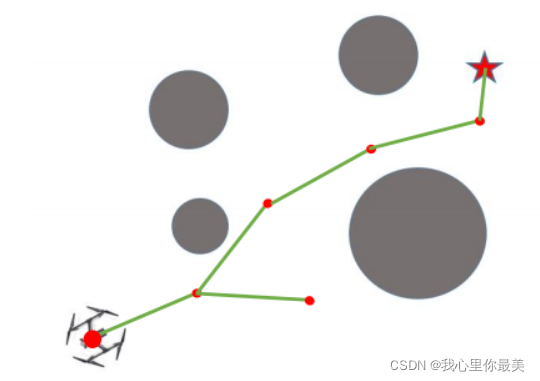
• 关键点：采样

  情况一：路径没有穿过障碍

  在地图范围内随机选取采样点，然后选取当前路径列表结点的最近点，以一定步长连接两点

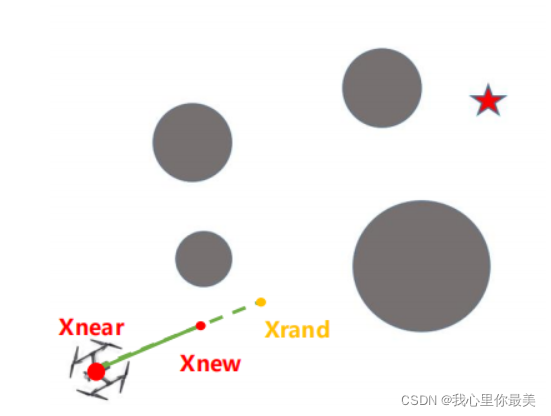
情况二：路径穿过障碍

需要舍弃该条路径选取

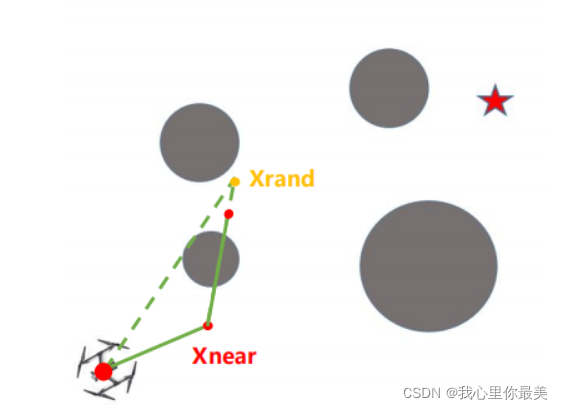
• 规范路径趋势

  赋予终点一定的概率被选作采样点，以规范路径使其趋向最优（尽管效果不佳）

• 动态步长优化

  连接两点之间的步长可以根据当前所处位置而动态变化，使路径更优

具体实现

伪代码：

主体核心代码+注释：

def rrt_planning(self, start, goal, animation=True):
        start_time = time.time()
        self.start = Node(start[0], start[1])
        self.goal = Node(goal[0], goal[1])
        self.node_list = [self.start]#把起点放入树
        path = None
        #rrt主体思想
        for i in range(self.max_iter):
            #采样点
            rnd = self.sample()
            #在self.node_list中获取near点
            n_ind = self.get_nearest_list_index(self.node_list, rnd)#返回near点的index
            nearestNode = self.node_list[n_ind]

            # steer：搭建树枝方向，以theta体现
            theta = math.atan2(rnd[1] - nearestNode.y, rnd[0] - nearestNode.x)
            newNode = self.get_new_node(theta, n_ind, nearestNode)

            noCollision = self.check_segment_collision(newNode.x, newNode.y, nearestNode.x, nearestNode.y)
            if noCollision:#noCollision=1表示树枝没有穿过障碍,记录path;否则舍弃这个newNode，继续sample
                #把newNode添加到node_list中
                self.node_list.append(newNode)
                #图像化仿真：显示寻找的过程
                if animation:
                    self.draw_graph(newNode, path)
                #判断newNode是否靠近goal：返回1则是
                if self.is_near_goal(newNode):
                    #是否穿过障碍
                    if self.check_segment_collision(newNode.x, newNode.y,
                                                    self.goal.x, self.goal.y):
                        #从0开始的下标，需要-1
                        lastIndex = len(self.node_list) - 1
                        #获取路线(找到的各个点的坐标)
                        path = self.get_final_course(lastIndex)
                        pathLen = self.get_path_len(path)
                        print("current path length: {}, It costs {} s".format(pathLen, time.time()-start_time))
                        #图像化仿真：显示最终路线
                        if animation:
                            self.draw_graph(newNode, path)
                        return path#返回整条路线

效果分析

• 搜索速度快
• 路径非最优
• 只能到达目标区域附近

2.RRT*

定义及适用场景

在RRT思想上寻找最优的路径

单源避障的最优路径问题

核心

• parent_node

  当前结点加入一步检索，寻找其到附近结点的最短距离，从而更新父节点，以使路径达到最优

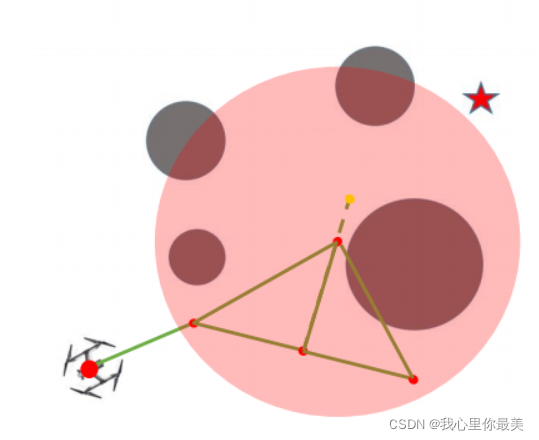
    def choose_parent(self, newNode, nearInds):
        if len(nearInds) == 0:
            return newNode

        dList = []
        #遍历每一个范围内的结点，判断障碍并计算距离
        for i in nearInds:
            dx = newNode.x - self.node_list[i].x
            dy = newNode.y - self.node_list[i].y
            d = math.hypot(dx, dy)#hypot(dx, dy) 求平方和的平方
            theta = math.atan2(dy, dx)
            if self.check_collision(self.node_list[i], theta, d):
                #正常，记录距离为原来路径长度加上这条树枝的长度
                dList.append(self.node_list[i].cost + d)
            else:
                #穿过障碍，记录距离为无穷大
                dList.append(float('inf'))

        minCost = min(dList)
        minInd = nearInds[dList.index(minCost)]

        if minCost == float('inf'):
            print("min cost is inf")
            return newNode
        #更新路径和距离
        newNode.cost = minCost
        newNode.parent = minInd

        return newNode

    def find_near_nodes(self, newNode):
        n_node = len(self.node_list)
        #范围圆的半径:随着node_list树结点的大小而动态变化的
        r = 50.0 * math.sqrt((math.log(n_node) / n_node))
        #遍历树结点，计算距离
        d_list = [(node.x - newNode.x) ** 2 + (node.y - newNode.y) ** 2
                  for node in self.node_list]
        #遍历距离列表，寻找 在范围内的点 在d_list列表中的下标index
        near_inds = [d_list.index(i) for i in d_list if i <= r ** 2]
        return near_inds#返回范围内点的下标

• rewire

  寻找到最优父节点之后在一定圆范围内不断检索所有临近结点的组合方式，重新组合路径，使其达到最优的效果

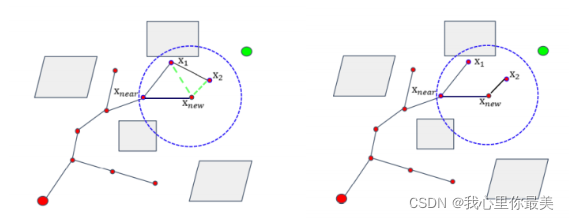
    def rewire(self, newNode, nearInds):
        n_node = len(self.node_list)
        for i in nearInds:
            nearNode = self.node_list[i]
            d = math.sqrt((nearNode.x - newNode.x) ** 2
                          + (nearNode.y - newNode.y) ** 2)
            s_cost = newNode.cost + d
            #如果附近结点(可选父节点)cost大于新选结点的cost，则更新临近结点的父节点和距离
            if nearNode.cost > s_cost:
                theta = math.atan2(newNode.y - nearNode.y,
                                   newNode.x - nearNode.x)
                if self.check_collision(nearNode, theta, d):
                    nearNode.parent = n_node - 1
                    nearNode.cost = s_cost

具体实现

                #两个优化技巧使路径趋向最优
                #寻找一定范围内的临近点(newNode的可能父节点)
                nearInds = self.find_near_nodes(newNode)
                #重新选择父节点:newNode的坐标不变，但cost和parent变了，即路径走向改变
                newNode = self.choose_parent(newNode, nearInds)
                #树中添加新结点信息，并且重新连接
                self.node_list.append(newNode)
                self.rewire(newNode, nearInds)

效果实现

• 搜索速度快
• 路径生成趋于最优
• 无效的搜索过多
• 只能到达目标区域

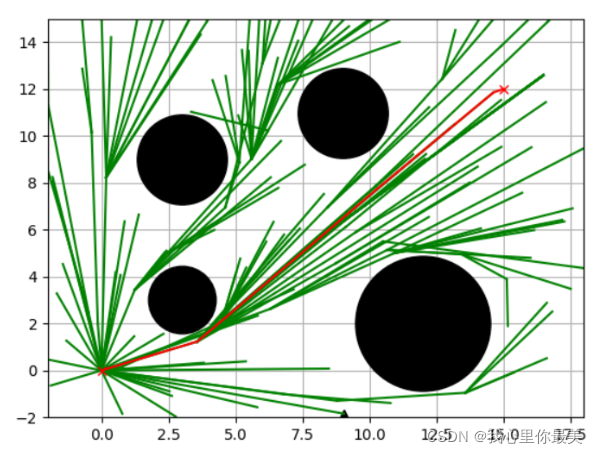
3.informed RRT*

定义及适用场景

在RRT*思想的基础上添加椭圆采样约束,优化路径、加快寻优速度

适用于单源快速避障的路径规划问题

核心

• 椭圆采样约束

  • 二维空间下，以起始点所有直线为椭圆长轴构建椭圆范围；三维空间下，构建椭球体

  • 确定Xcenter点，作为坐标系转化的偏置修正

  • 计算起始点的起始距离作为Cmin

  • 每次采样前，计算当前路径的代价长度作为Cbest；计算旋转矩阵Kabsch算法求解旋转矩阵

  • 每次采样时，以单位圆的形式采样获取坐标Xball；计算r矩阵、C旋转矩阵

  • 每次采样后，以公式 rCXball+Xcenter 转化为椭圆坐标系下的坐标

    重点：不断缩小椭圆的范围

    具体实现：Cbest是在迭代中不断更新变化的，设置r矩阵第一个元素为Cbest的一半，第二个元素是Cbest与起始点长度的平方和的开方的一半，因此椭圆范围会不断更新变化（缩小）

• 旋转矩阵

  计算旋转矩阵Kabsch算法求解旋转矩阵

具体实现

    def informed_sample(self, cMax, cMin, xCenter, C):
        if cMax < float('inf'):
            # L矩阵第一个元素为长轴的一半，第二个元素是当前路线长度与起始点长度的平方和的开方的一半
            r = [cMax / 2.0,
                 math.sqrt(cMax ** 2 - cMin ** 2) / 2.0,
                 math.sqrt(cMax ** 2 - cMin ** 2) / 2.0]
            L = np.diag(r)#生成以r为元素的对角矩阵
            #生成采样点(以单位圆内采样)
            xBall = self.sample_unit_ball()
            #压扁为在椭圆范围内
            rnd = np.dot(np.dot(C, L), xBall) + xCenter
            rnd = [rnd[(0, 0)], rnd[(1, 0)]]
        else:
            #未生成椭圆
            rnd = self.sample()

        return rnd#返回采样点的坐标

效果实现

• 渐进寻优速度加快
• 路径趋向最优的效果极佳
• 减少了无效的搜索

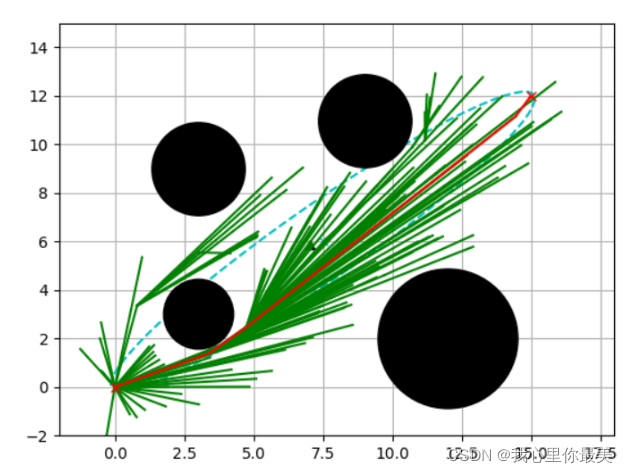
4.PRM

定义

以随机采样的形式采点，当代价<阈值时，生成点与点之间的直线路线，最后在搭建的路线图中寻找最优路径

概率路线图构建

• 随机采样

• 采样点和距离<阈值，则生成路线连接

图上寻找最优路径

以代价最低为目标寻找最优路线即可

（三）基于启发式智能算法的路径规划

1.遗传算法

2.蚁群算法

由于实际应用中较少，且以往已经接触和实现过，故在此不做笔记

三、经典算法的代码实现

• 代码的实现参考了IR艾若机器人的算法思路，深入理解了算法的核心部分

• 由于算法应用于不同的问题有不同的逻辑，故后续需要在不同问题场景下或者ros下跑一下仿真

  （未完待续…）

四、经典算法的适用场景总结

五、论文泛读—算法改进

（另写一篇文章，未完待续…）

后记

入门路径优化算法√

人生之悟

路径虽有规划之法，但人生路毕竟多变，还需不断提升应变能力才能达到更好的下一个起点（人生没有终点）

人生路如此，无人机路径也如此，飞行环境多变，故此需要学习和探索应对多变环境的方法，使其增强生命的硬度！！！！