[数据结构与算法]Codeforces Round #769 (Div. 2)：E1. Distance Tree (easy version)

距离树

能力有限，只看懂了easy version…

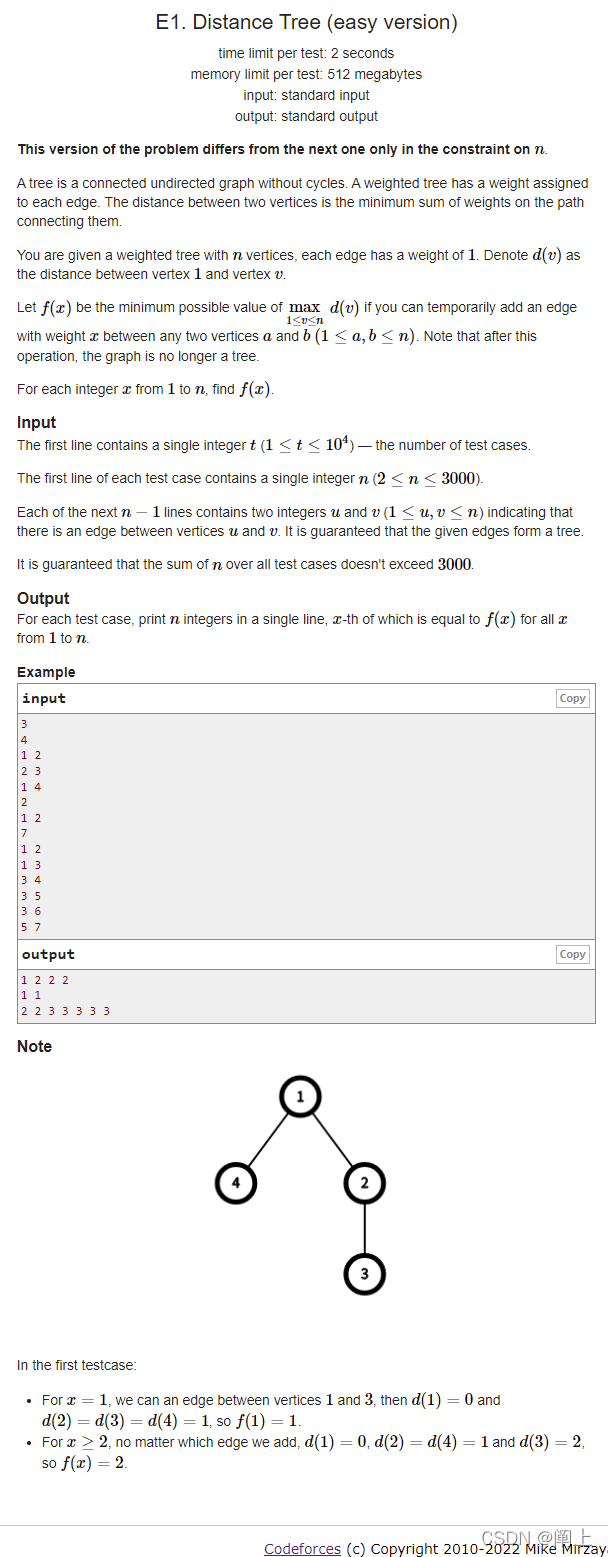
题意：

• 给定一颗 n 个结点的树，$d(v)$代表这颗树上任意点到 1 点的最短距离
• 定义$f(x)$表示：在这棵树上任意两点间加一条权值为 x 的边后，$Ma{x}_{1<=v<=n}d(v)$的值
• 对于所有的 x 取值于1~n ，求出对应$f(x)$
• 分析：在树上如何加一条边，能使得各个点到 1点 的最短距离最大值最小

思路：

• 加边最优的操作显然是 某点连向 1，这个可以自行纸上模拟；
• 我们加边的操作不能只顾及极限点，比如离 1 最远的点；只修改最远点到 1 的距离，不顾及次远点、次次远点是不妥当的；
• 为了使最大值最小，我们最好把 这个加边点 放在 树的中心，每个点到该点的最短距离都相较平均，题解的意思如此，具体证明不能 ；

基于以上前提，题解给了一种很神必的枚举方法 —— 枚举答案（二分答案没了二分 ）

我们每次都假设一个 ans 答案，表示加边后 1 点到最远点的 距离，若加边点是在树的中心上，因为 树的中心 == 树的直径中点 ，我们能得知 树的直径 == $2?(ans?x)$

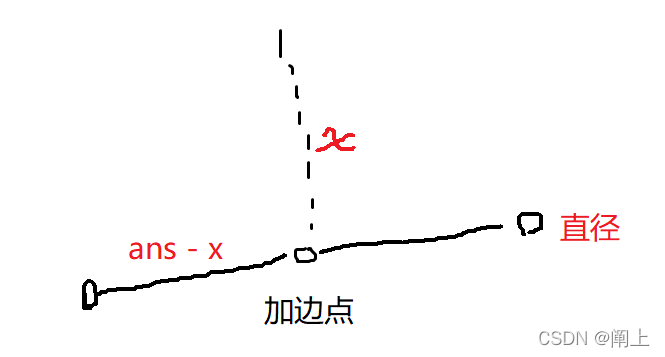
在该答案的限制下我们去求 树的直径 为多少，即可判断此时 ans答案 是该保留还是增大（尽可能取小）

是不是跟二分答案很像？

至于限制是什么，限制就是：

• 若当前 ans == 2，我们求 树的直径 时就不能枚举到 深度dep（离1点距离）<= 2 的点，也就是直径两端的点不可以是这些点，因为这些点可以直接走到 1 上，不影响 ans，加边点的放置是为了优先考虑直径两端的极限点，减少极限点到 1 的距离
• 很玄学的解释，有更好的说法可以交流一下

最后，cf 给的题解是$O(n^3)$的…亲测极限情况会被 链状树 数据卡成 4s，但出题人好像没出这种数据 如果是我搞错了请指导我

这里给一种排序预处理、指针遍历的做法，稳定$O(n^2)$

$Code:$

#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul (u << 1)
#define ur (u << 1 | 1)
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define rfor(a,b,c) for(int a=b;a>=c;a--)
//#define x first
//#define y second
//[博客地址](https://blog.csdn.net/weixin_51797626?t=1) 
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int> PII;

const int N = 3010, M = 6010, MM = N;
int INF = 0x3f3f3f3f, mod = 1e9 + 7;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int h[N], e[M], ne[M], idx;
int d1[N], depdis[N];
struct node
{
	int w, id;
	bool operator<(const node& no)const { return w > no.w; }
}dd[N];

inline void add(int a, int b) {
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int x, int fa, int* d) {
	for (int i = h[x]; ~i; i = ne[i]) {
		int j = e[i];
		if (j == fa)continue;
		d[j] = d[x] + 1;
		dfs(j, x, d);
	}
}

void solve() {
	cin >> n;
	idx = 0;
	forr(i, 1, n)h[i] = -1;//注意按数据初始化，memset不要乱用

	forr(i, 1, n - 1) {
		int a, b;
		cin >> a >> b;
		add(a, b), add(b, a);
	}

	int d_dep = 1;//记录离1最远的点
	d1[1] = 0;
	dfs(1, -1, d1);
	forr(i, 1, n)if (d1[i] > d1[d_dep])d_dep = i;

	depdis[d_dep] = 0;
	dfs(d_dep, -1, depdis);//跑一个其他点到最远点的距离

	forr(i, 1, n)dd[i] = { depdis[i],i };//用数组记录下来
	sort(dd + 1, dd + 1 + n);//从大到小排序
	//最大的肯定是树的直径，如果直径的一个端点被覆盖了就舍去，找次直径

	forr(i, 1, n) {
		if (d1[d_dep] <= i) {//如果加的边没有贡献就直接走人
			cout << d1[d_dep] << ' ';
			continue;
		}
		int j = 1, ans = 0;//否则枚举答案
		while (1)
		{
			int max_dist = -1;
			//在此刻被限制的直径，ans变大后肯定也被限制，所以可以指针只跑一遍不循环
			while (j <= n) { 
				int id = dd[j].id;
				if (d1[id] <= ans)j++;//限制
				else {
					max_dist = dd[j].w;
					break;
				}
			}
			if (max_dist == -1)break;//如果找不到说明已经没法更新ans了，退出

			if (max_dist > 2 * (ans - i))ans++;
			else break;//同理
		}
		cout << ans << ' ';

		//预处理能保证两个while循环独立
	}
	cout << '\n';
}

int main() {
	cinios;

	cin >> T;
	while (T--)solve();

	return 0;
}
/*
*/